- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Phi in DNA structure
1.- Introduction
This article is devoted to the dimesions of the DNA molecule based on the research by Mark E. Curtis [1]. It is well known that each complete turn of the DNA double helix measures 21 amstrongs wide by 34 amgstrongs long. 34 and 21 are two consecutive numbers in the Fibonacci series. Therefore their ratio, 1.6190476 closely approximates the Golden Ratio φ=1.6180339...
Almost 20 years ago, Mark E. Curtis began an investigation into the structure of DNA with the intention of producing a series of drawings and paintings of the double helix [1]. He embarked on scale drawings of the helical structure using the standard textbook dimensions that derive from x-ray diffraction data. In the course of his work, discrepancies emerged, and it became clear to him that the Crick and Watson structure [2] did not conform to geometric principles. Indeed his attempts to translate their theory from 2D into 3D ran into considerable topological problems. He discovered that a growing minority do recognise flaws in Crick and Watson’s conclusions, specifically in terms of its topology and thereby the ability of the structure to replicate itself. Although some research has even gone so far as to question the very existence of the double helical structure itself, his proposal retains the double helix as its fundamental basis.
Without compromising the essence of their structure, Mark E. Curtis proposed a resolution of the geometrical inconsistencies by means of a simple change in the position of alignment between the purines and pyrimidines. This realignment is founded entirely upon geometric principles. Furthermore, a set of simple mathematical relationships involving Sacred Geometry describe a three-dimensional geometric helix that conforms to the known ratios of DNA. This re-reading of DNA engenders a high simplicity and purity when applied to the molecular structure of the bases.
2.- Sacred Geometry under the DNA molecule
Theoretically, it is possible to construct a helix from almost any series of polygons, there happens to be only one polygonal formation that would fulfil all the necessary criteria: ten regular pentagons orientated about a decagon (Figure 1).
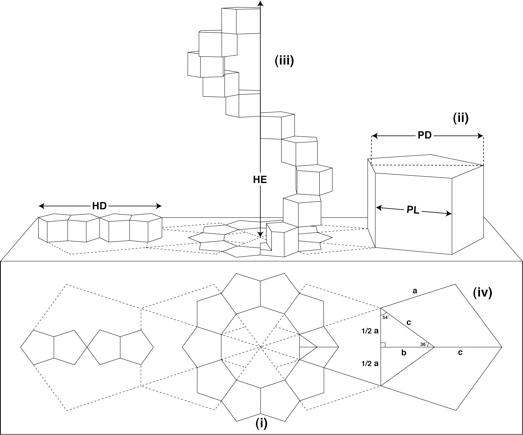 |
| Figure 1: Geometric structure of the DNA based on Sacred Geometry (reproduced from [1]): |
When translated into 3D, these pentagons would become prisms with all lengths equal (ii). A complete turn of the helix is formed by progressive rotation and extension of the ten regular pentagonal prisms (iii). The diameter of the helix (HD) and the height of the helix extension (HE) have a direct and constant proportional ratio to the pentagon edge length (PL) and the pentagon height (PD).
From the preceding figure, PL=a and PD=b+c obeys the following expression:
from which the exact values of PD, HD and HE can be numerically dermined:
PD = 1.5388417686·PL
HD = 4·PD = 6.1553670744·PL
HE = 10·PL
Let's apply one of the known dimensions of the DNA to the above equations. The base height is known to be aproximately PL=3.4Å. Therefore we have
PD = 1.5388417686·PL = 5.23206201324 Å
HD = 6.1553670744·PL = 20.928248053 Å
HE = 10·PL = 34 Å
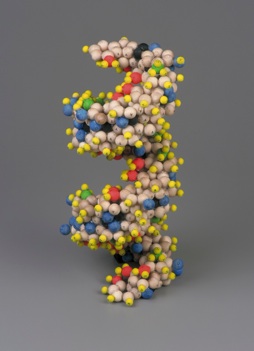
These figures seem to cohere with the known dimensions of DNA as revealed by x-ray diffraction data. From this, Mark E. Curtis constructed the following exact dimensional composite of the DNA double helix (Figure 2). He used single pentagonal prisms to illustrate the 3-dimensional helix. However, to ensure stability in the structure as it would exist in reality, it is necessary to place adjacent pentagons on each plane and then stack accordingly, thereby creating the double helix:
 |
 |
| Figure 2: Geometric model of the DNA double helix by Mark E. Curtis (reproduced from [1]) | |
3.- Application of geometry to the DNA molecular structure
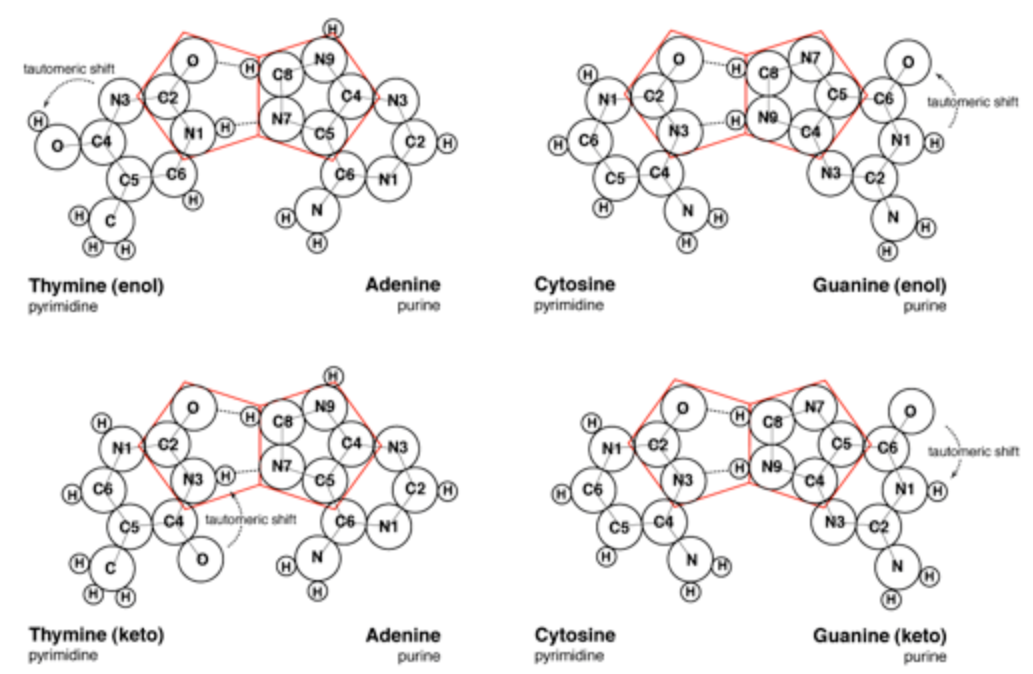
The pairing of purines and pyrimidines in the Crick and Watson proposal locates the molecular pentagons that make up a part of the purines on the outside of the paired bases (Figure 3). However, it has been demonstrated that a more fluent and natural geometry would require adjacent pentagons at the heart of the base pairing. Therefore Mark E. Curtis proposes to re-orientate the established molecular pairing, so that the pentagons of adenine (A) and guanine (G) form hydrogen bonds to the hexagonal structures of both thymine (T) and cytosine (C) (Figure 4). This spatial arrangement of the hydrogen bonds enables the necessary adjacent second pentagon to become viable. Moreover, it also accords with our understanding of molecular bonding and maintains the specificity of G with C and A with T.
 |
|
|
(a) Crick and Watson base pairings [1]. |
|
 |
|
|
(b) Curtis proposed pentagonal pairings [1]. |
|
| Figure 3 |
At this point, Mark E. Curtis refers to the different formations that the molecules of guanine and thymine can take, namely the enol and keto states. Guanine and thymine may exist in either enol or keto configurations and are believed to pass through tautomeric shifts from one to the other. In other words, an indiscernible and spontaneous leap by the hydrogen atom from a specific oxygen atom to a specific nitrogen atom or vice-versa. The Crick and Watson proposal requires the keto formation, whereas Curtis alternate proposal is viable in either of the formations.
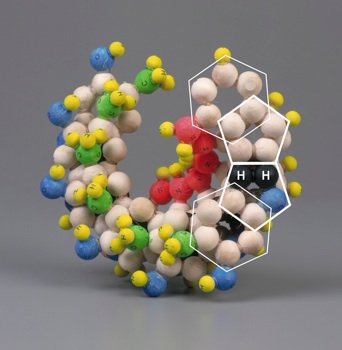 |
 |
| Figure 4: Three dimensional costruct showing the base modifications proposed by Mark E. Curtis [1]. | |
4.- Implications of the model
The structure for DNA proposed by Mark E. Curtis is wholly founded upon mathematical principles. Although the geometrical modification to the base pairings is relatively minor, the resulting double helix manifests a clarity altogether distinct from that offered by Crick and Watson, and it would appear to shed light upon a number of areas of continuing uncertainty.
The implications of these findings are inevitably far-reaching and would potentially affect many areas of research. The principal features of this proposal are:
- Geometric equations predict the dimensions of DNA’s structure. Not only does the pentagonal geometry predict the helical dimensions but it would also demonstrate ‘principle causation’.
- The pentagonal geometry provides the dynamics required to build a consistent, stable and uniform helical structure and also establishes why there should be consistently ten bases contained within a single turn of the helix. Incidentally, when converted to the molecular dimension Curtis predicts degrees of variation, certainly between 9.5 and 10.5 bases per turn, but perhaps even more.
- Both the hollow centre and side-by-side structural formation ensure instant access at any point within the helix. This would permit the DNA (even circular) to open and close during its replication functions without entangling itself.
- The modification to the base pairing would appear to be able to exist in either the enol or keto formations.
- While the sugar-phosphate backbones will undoubtedly prove integral to the stability of the helical structure, it is the geometry of the base-pair molecules themselves that is ultimately responsible for the formation of the helix.
5.- References
[1] Mark E. Curtis, "The geometry of DNA: a structural revision".
[2] Crick, F. H. C. & Watson, J. D. (1953) Nature, vol 171, 737-738.
