- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
The Golden Trisection
1.- Introduction
The readers of this site are already familiar with the Golden Ratio. We have explored many of its properties and applications. We have also seen that it is a member of a family of special numbers usually known as Metallic Means, which have a continued fraction representation of the type [p; p, p, p, ...]. In this article, we explain how the Golden Ratio can also be generalized from the geometrical instead of the numerical point of view. As the Golden Ratio is related to the unit pentagon, its direct generalization will be related to the unit edge heptagon.
Consider the pair of numbers 1.80194 and 2.24698. Let's see that they are as special as our familiar φ = 1.618033... If you take the product of them, you will see that it coincides with their addition: 1.80194 · 2.14698 = 4.04892 = 1.80194 + 2.14698. The square of the first equals the second plus one: 1.801942 = 3.24698 = 2.24698 + 1. The square of the second is one more unit of the addition of both: 2.246982 = 5.04892 = 1.80194 + 2.24698 + 1. Note the similarity with φ2 = φ + 1 and with φ2·φ = φ2 + φ. If you divide the second by the first, you get the first minus one unit: 1.80194 / 2.24698 = 0.80194 = 1.80194 - 1. And the same happens in the reverse way: 2.24698 / 1.80194 = 1.24698 = 2.24698 - 1. Compare them with 1/φ = φ/φ2 = φ - 1. So we can see that this pair of special numbers exhibit similar numerical properties as the Golden Ratio: they turn multiplications and divisions into additions. The question we will try to answer in the following sections is whether they are optimum in some way, and what is their geometrical interpretation.
2.- The heptagon diagonals
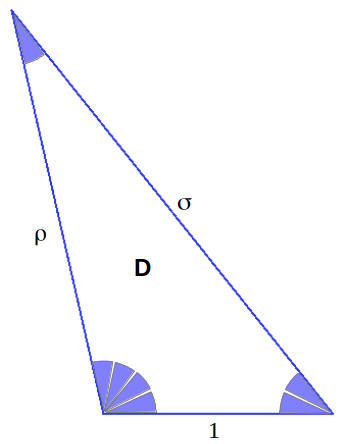
The Golden Ratio is the diagonal length of a unit edge pentagon. Similarly, we are going to show that the pair of special numbers shown above, from now on called ρ and σ, happen to be the diagonal lengths of a unit edge heptagon:
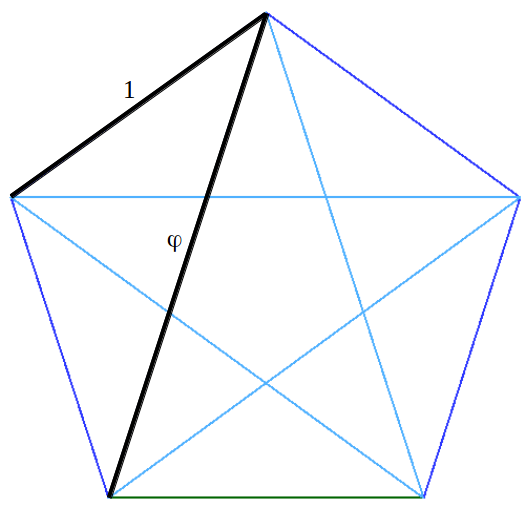
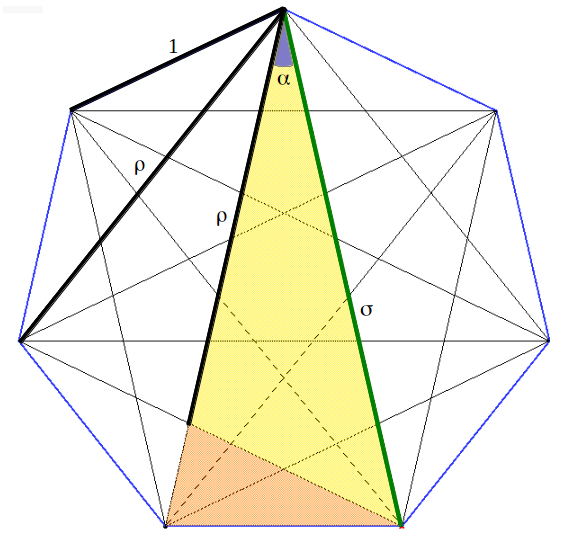
By symmetry, it is easy to see that all the inner angles α of the heptagram are equal. Taking into account that the angles of the triangle must add up to π, this angle must be α=π/7. If we take these facts into account and we extract the coloured triangle from the heptagram, we are able to easily calculate the exact values of ρ and σ using the sine theorem:
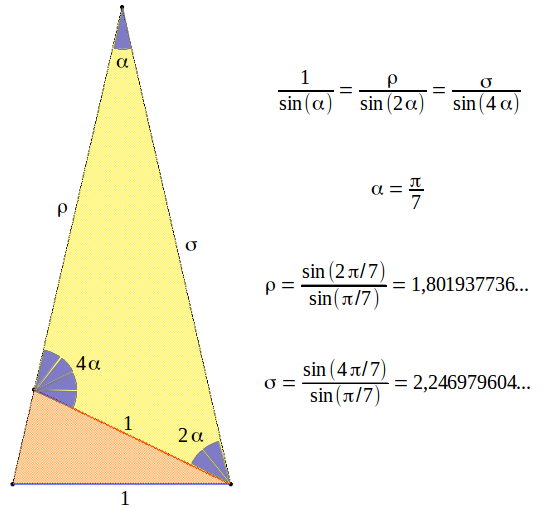
Mathematicians would probably say: "this is a straightforward generalization of the diagonal formula of a pentagon to an heptagon. But this does not show any relationship with the Golden Ratio as the optimum way of cutting a segment into two halves". So the question still is: how do these two magic numbers ρ and σ relate to optimum proportions within a segment? This is the relationship that Peter Steinbach happened to discover by chance [1],[2]. Before going deeper into this matter, we must introduce the concept of a three by three proportion.
3.- A three by three proportion
Consider a shoe box without its cap. Imagine you wanted to build two bigger replicas of it of different sizes: once twice as big, and the other three times bigger. Then you would be faced with a three by three proportion. The original dimensions (height H, width W and depth D) would have to be proportionally preserved in both constructions, with the apropriate conversion factor (or scale) in each case. This can be mathematically expressed as:

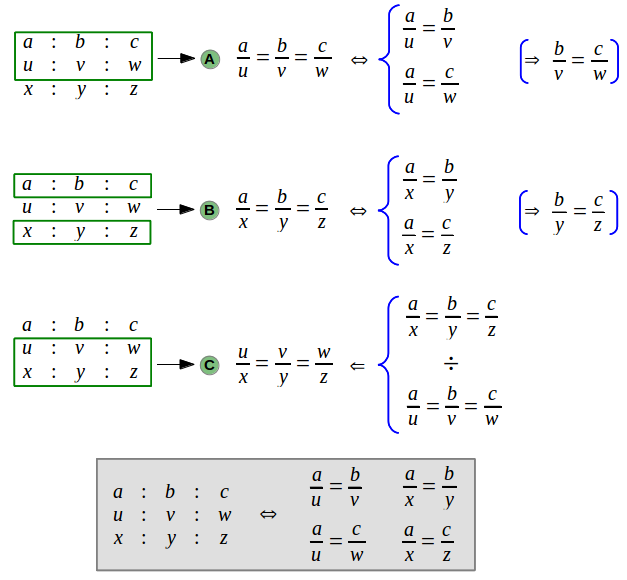
Imagine that now we are faced with a set of nine numbers (a, b, c; u, v, w; x, y, z) and we want to check if they meet a three by three proportion. In a first approximation, we would check nine individual quotients: (A) the elements of the first row with the elements of second one, (B) the elements of the first one with the elements of the third one, and finally (C) the elements of the second one with the elements of the third one. However, if we look at the three by three proportion more carefully, we see that it suffices to check only four quotients. Then the remaining five will be authomatically satisfied:
4.- The Golden Trisection
We have seen in our previous article that the Golden Ratio cuts a segment in two pieces that fit a two by two proportion, in a way such that the whole is to the larger part as the larger is to the smaller part. Now, what proportions can be made by multiple cuts of a segment? The first generalization is to make two cuts. This way we create six segments: the three parts, the whole, and the sum of the middle and the left or right part. Peter Steinbach then asked himself: "Is there some extended proportion that can be satisfied by six such lengths?" The answer lays in the following figure, which shows the optimum trisection of a segment. It is the best possible in the sense that it is the unique optimally proportional trisection analogous to the Golden bisection. By optimal we mean: "just as there is no cut other than the Golden Ratio that fits a non-trivial proportion, so there is no pair of cuts other than the ones shown in Figure 2 that yield an equal or greater harvest of proportions" [2].
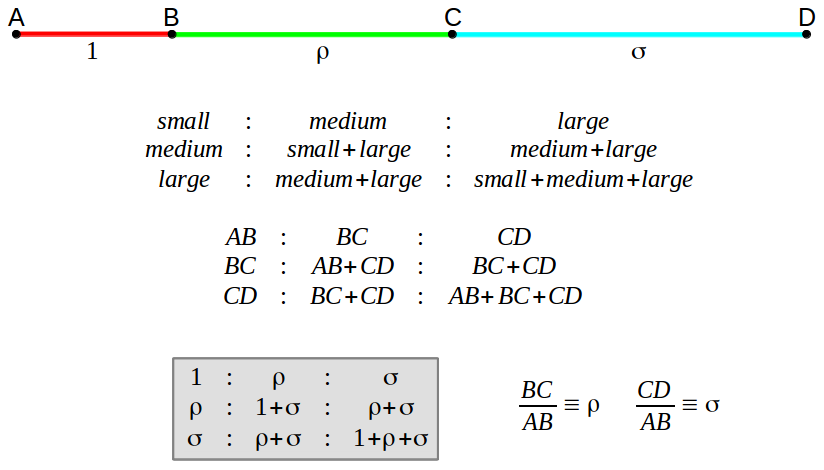
By normalizing the calculations to the length of the first section AB, we see that it suffices to find the quotient of the remaining to sections BC and CD with the first one, which we have also called ρ and σ. In order for these two numbers to trully satisfy a three by three proportion, they must meet the set of four equations shown in section 3 above (sets A and B). Taking the first two rows in the proportion, we get the first set of equations that have to be satisfied:
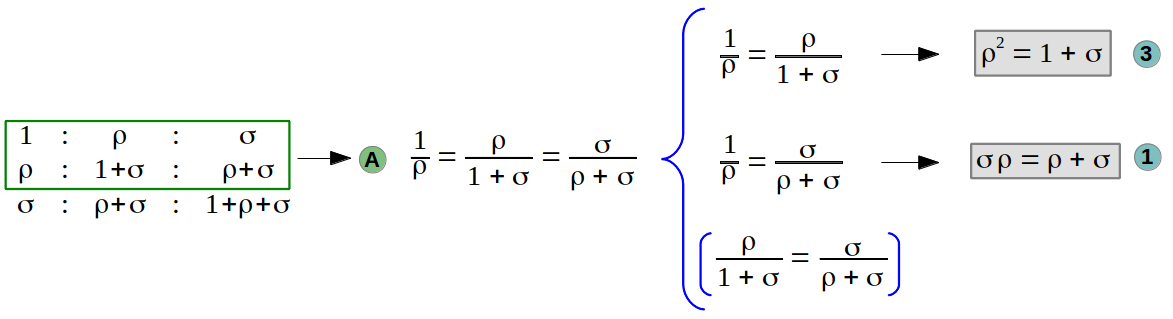
Making the same with the first and the last rows, we get the second pair of equations. As shown in section 3, notice that we don't need to check any other quotient: if these four equations are met, then all nine quotients in the three by three proportion will be satisfied.
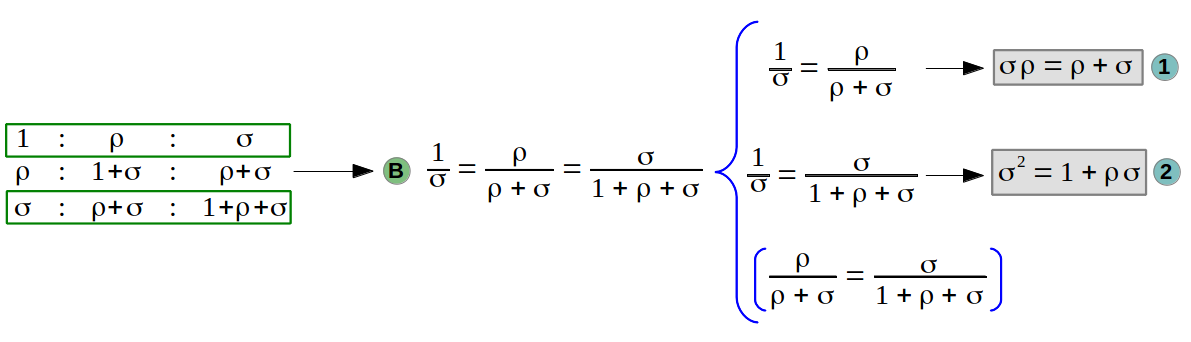
What the previous analysis shows us is that, actually, there are only three equations that need to be satisfied. In fact, with a bit of algebra it can be demostrated that any two of those three equations are enough (that is to say, the third one can be derived from the other two). This can be elegantly shown graphically. In the following graph we plot equations 1, 2 and 3 in the ρ-σ plane. We can see that any pair of curves (either the green-red pair, or the green-blue pair, or the red-blue one) intersect in exactly the same three points. This plot also shows the positive solution to these equations. As you might expect, their numerical value coincides with the diagonal lengths of the unit edge heptagon!
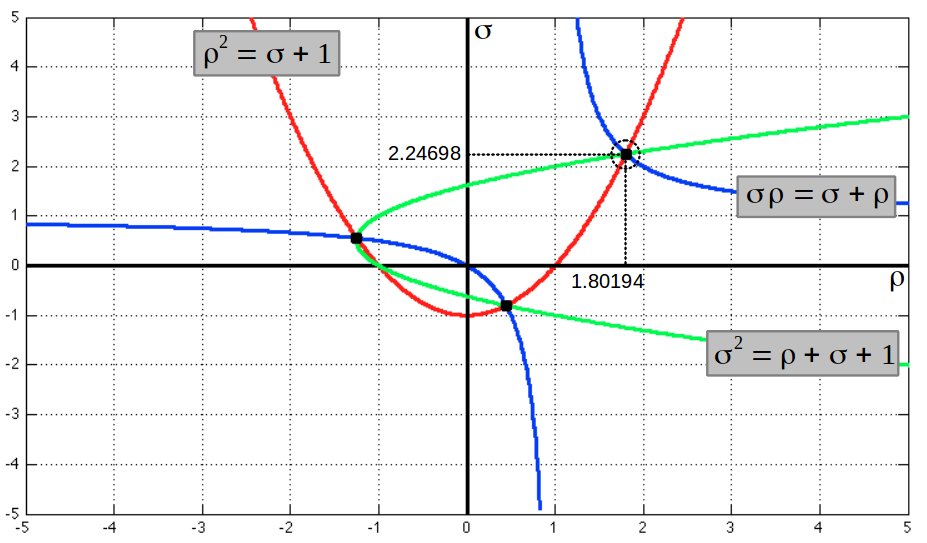
The numerical solution of these equations can also be obtained separately for ρ and σ if we notice that they satify two cubical equations:
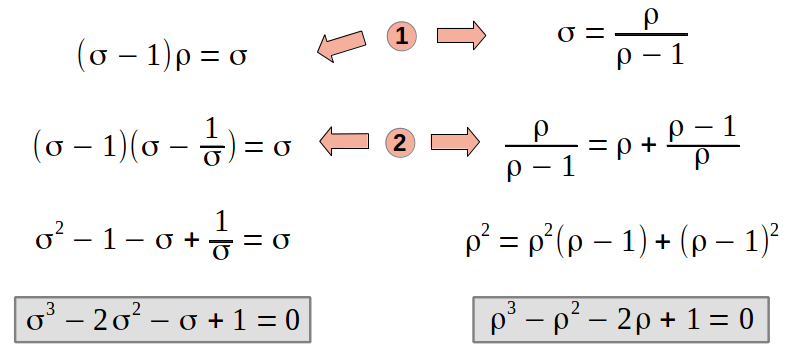
These equations do not have a closed formula solution as it happened with the Golden Ratio. We have to solve them numerically to find out that ρ=1.8019377... and σ=2.24697960... are the solutions that we were looking for. More generally, it can be shown [1] that the cubic polynomial x3-x2-2x+1 has roots ρ, 1/σ and -σ/ρ; and the polynomial x3-2x2-x+1 has roots σ, 1/ρ and -ρ/σ (compare with the intersections of the curves in the graph above). Here we have a "numerical" proof that the Golden Trisection of a segment can be geometrically found in the diagonals of a unit edge heptagon. However, in what follows we will show these diagonals actually meet exactly the same equations 1 and 2 as the Golden Trisection of a segment. This will constitute the analytical proof that we are looking at the same phenomena from two different points of view.
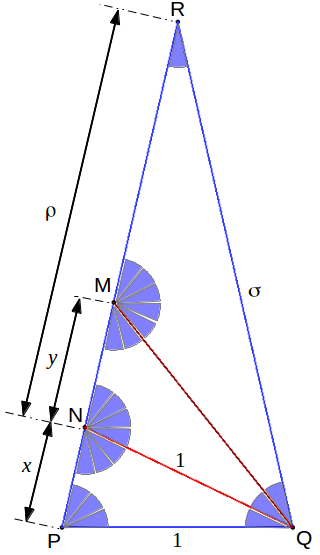
Let's pick the central heptagram triangle including all of its diagonal segments. The following figure shows also all of its angles. The lengths to be determined are x and y. The only thing we have to notice is that there are several similar triangles, smaller ones inside bigger ones. Then the required equations follow by similarity:
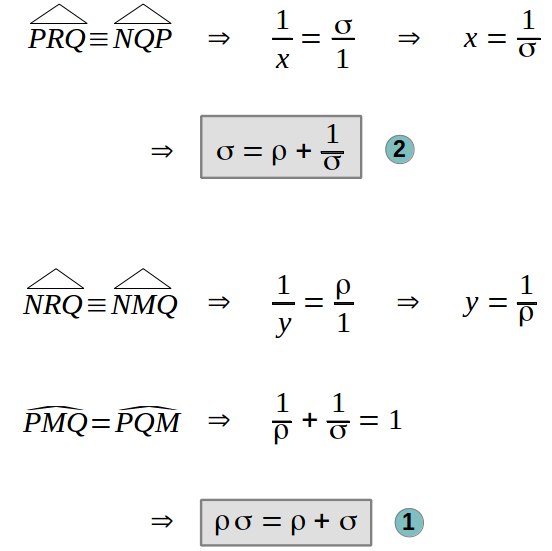
5.- To add is to multiply
The numbers is this optimal family (φ, ρ, σ, ...) have remarkable properties. Artists have made extensive use of the fact that simlar figures with these proportions can be arranged easily and can be dissected into sets of similar figures. "This is the origin of the Greek idea of geometric progression - that multiplication can be accomplished instead of addition"[2]. As it is well known that the square of the Golden Ration is one more than itself (φ2 = φ + 1) and that one less equals its inverse (1/φ = φ - 1), the heptagonal diagonals or Golden Trisection ratios also have similar properties, which can be derived from equations 1, 2 and 3 as follows:
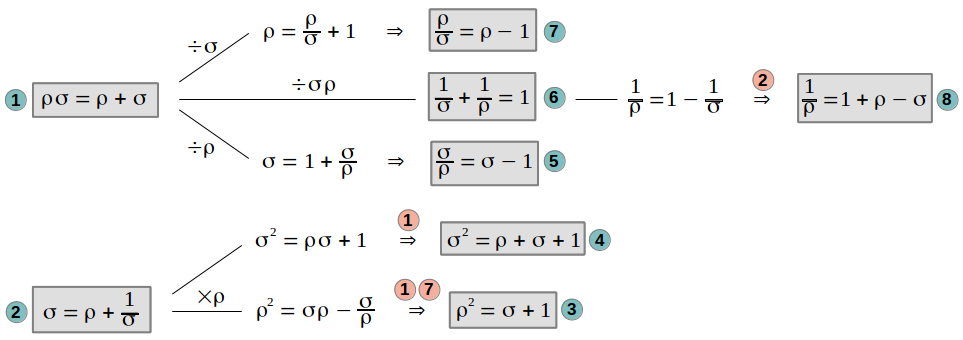
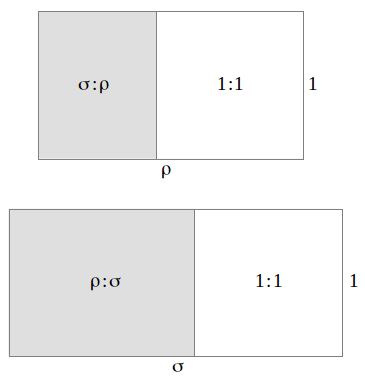
These are precisely the surprising properties that we checked numerically in the introduction. A visual analog of these equations is found in the following figure, where we can observe that removing a square of a rectangle of proportions 1:ρ or a 1:σ leaves another rectangle of proportions ρ/σ in different orientations. Further visual examples can be found in references [1] and [2]:
6.- The Golden Trisection in the Heptagon
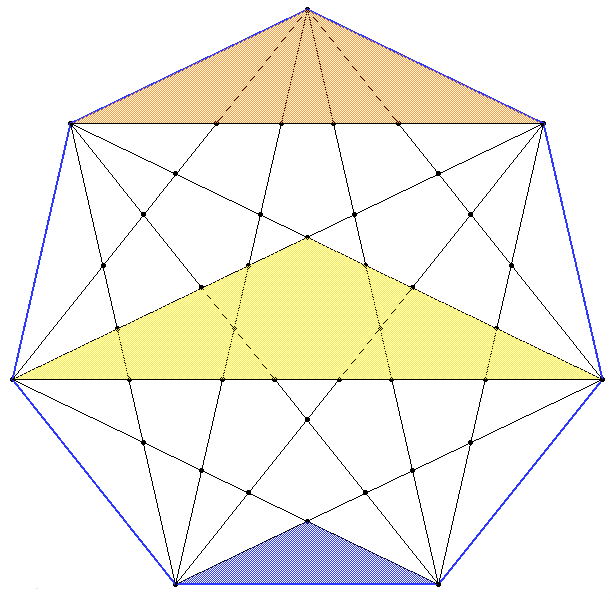
The heptagram contains four different triangle types which include different ρ and σ proportions, depending on their angles that are always multiples of α=π/7.
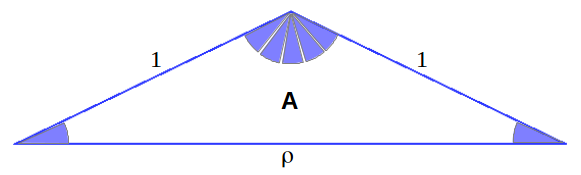
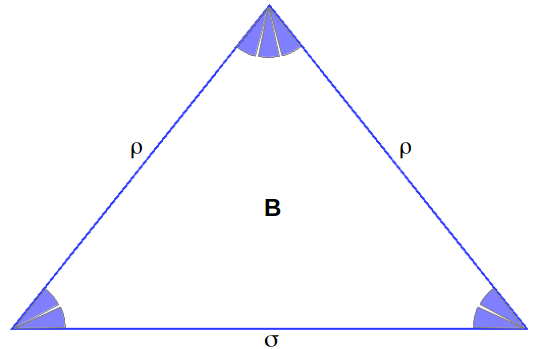
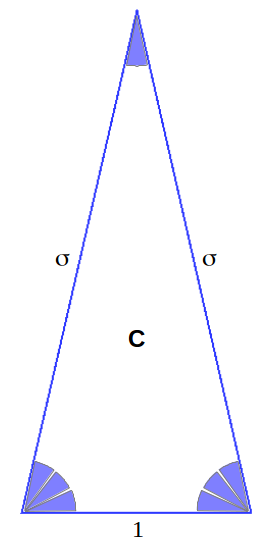
These triangles can be found in different sizes in the heptagram, as shown in colours in the folloing figures. We leave the deduction of the proportions in each triangle to the reader (the heptagram shown later on can be of help):
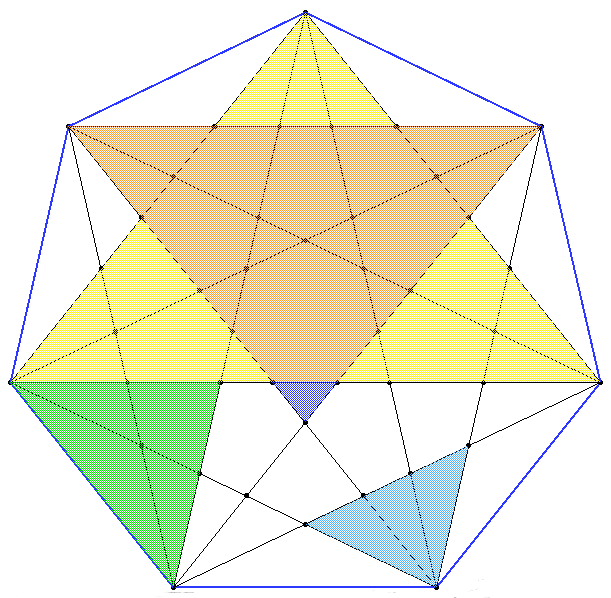
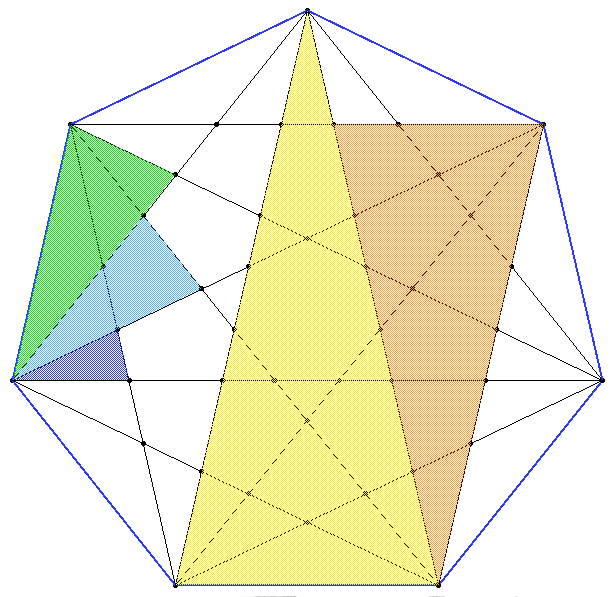
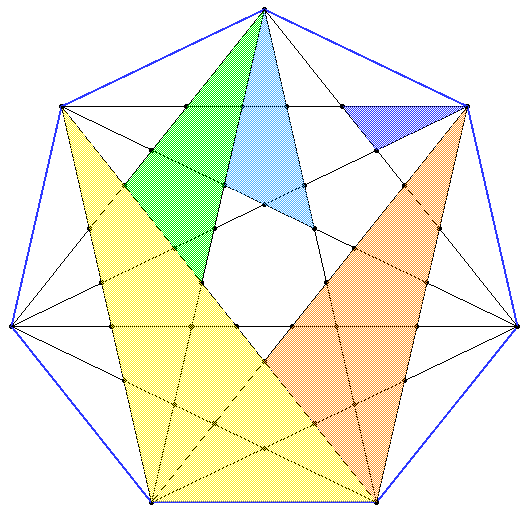
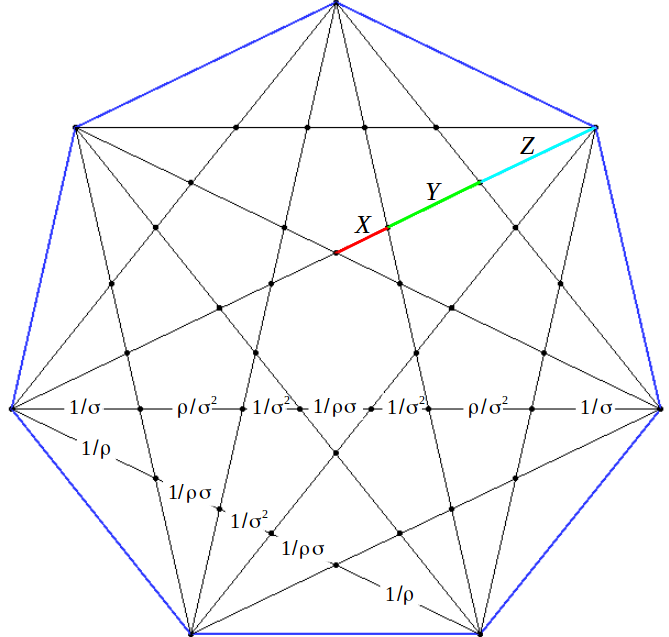
Working out the similarities of these triangles you can arrive at a way of dividing the small (ρ) and long (σ) diagonals of a unit edge heptagon in terms of fractions proportional to these lengths. As an integration of the two ways of looking at magic numbers ρ and σ, we also show the Golden Trisection inside the heptagon (notice that X : Y : Z = 1/σ2 : ρ/σ2 : 1/σ = 1 : ρ : σ).
7.- Rational approximations
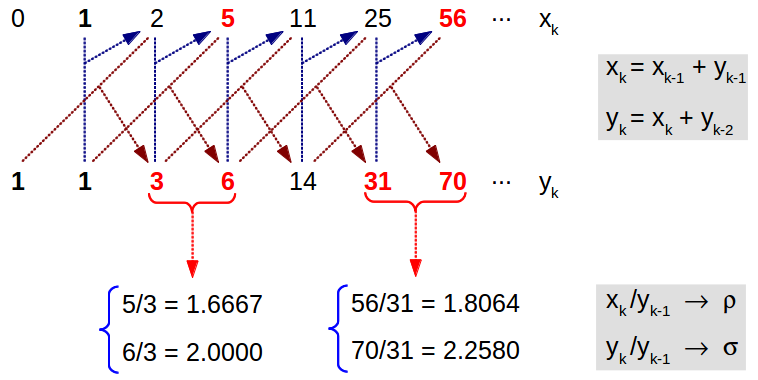
Finally, we can't close this article without making a connection with the rational sequences that allow approximating our magic ratios φ, ρ and σ. As we know, the Fibonacci sequence offers a stepwise approximationg method to the Golden Ratio. This sequence is also connected with the successive powers of φ. In a similar way, there exist a pair of interwined sequences {xk} and {yk} which provide rational approximations to ρ and σ. Starting with three number ones as shown below, we can get the next element in the first sequence by adding the previous element in both sequences (xk=xk-1+yk-1), and the next element in the second sequence as the current element in the first sequence plus two elements before in that sequence (yk=xk+yk-2). After completing any step in this process, the ratio of the elements in each sequence with the element in the first one provides a rational approximation to ρ and σ respectively. These pair of sequences are called by some authors 3rd order Fibonacci sequences:
There exist a family of matrices that allow an easy computation of those sequences by matrix multiplication. They are known as Golden matrices, and can be simply built by a triangle of ones perpendicular to the matrix diagonal. Let's see this matrix in action for the case of the Golden Ratio:

As we can appreciate, dividing all the elemts of the mtrix by the first element provides a rational approximation to the Golden 2x2 proportion. In a similar way we can calculate the Golden Trisection matrices:

Again, we obtain rational approximations to all the members of the Golden 3x3 proportion by dividing all the matrix elements by the first element. The higher the power of the original Golden matrix, the closer the approximation to the exact proportion.
As the reader might suspect, this process does not stop in the 3x3 case. The 4x4 Golden matrix provides a way of calculating the 4th order Fibonacci sequences. And what are these sequences approximating? Well, nothing more and nothing less that the optimal quadrisection and proportion of a segment, which of course is another way of looking at the diagonals of a unit edge enneagon. Peter Steinbach has continued this process up to the pentasection (5x5 proportion) using the diagonals of the unit edge 11-gon. He states that "this is the largest known unique optimally proportional section, and there is as yet no mathematical proof that uniqueness continues indefinitely" [2].
As a concluding paragraph, we would like to quote him when he says:
"Considering the prevalence of the golden proportion and the Fibonacci sequence in the growth of natural forms, one wonders whether these other ratios and sequences occur in nature. Flower symmetries, for example, occur mainly in 4-, 5-, 6- 7- and 8-fold types, and algebraic numbers asociated with all but one of these types -the heptagon- have been widely studied in a great variety of natural contexts. Has the heptagon been overlooked? Can ρ and σ be found in plain view?"
References
[1] Steinbach, Peter: "Golden Fields: A Case for the Heptagon", Mathematics Magazine, vol.70, no. 1, February 1997.
[2] Steinbach, Peter: "Sections Beyond Golden", Bridges: Mathematical Connections in Art, Music, and Science, 2000.
Last updated: 2015/08/09
