- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Pyramids and Prisms
1.- Pyramids
A pyramid is a polyhedron formed by connecting each vertex of a polygonal base to a point called the apex. It is a conic solid with polygonal base. When unspecified, the base is usually assumed to be square. If the base is a regular polygon and the apex is perpendicularly above the center of the polygon, the pyramid is symmetric. The segment that connects the apex to the midpoint of a base edge is called the apotem (Figure 1).
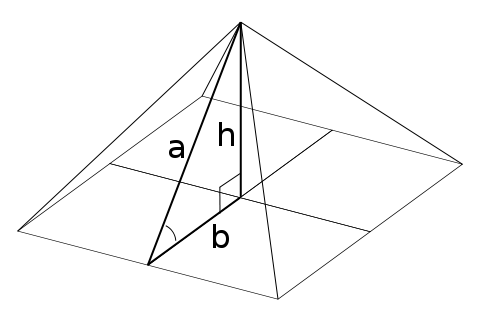 |
| Figure 1: A general square pyramid of base 2b, height h and apotem a. |
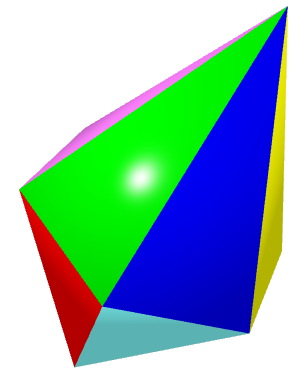
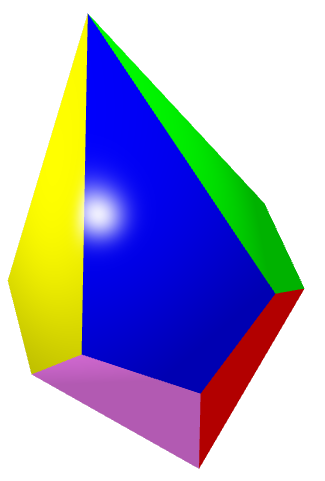
There are only three pyramids whose bases are a regular polygon ang whose edges are all equal: the tetrahedron, the square pyramid and the pentagonal pyramid (Figure 2).
 |
 |
 |
| (a) Triangular | (b) Square | (c) Pentagonal |
| Figure 2: Pyramids with regular polygonal base and equal edges (click on the image to get a 3D view that you can zoom and rotate). | ||
In general, given a regular polygonal face, the pyramid's height can take any value. However, there are some special square pyramids, such as the Golden pyramid, in which the b:h:a triangle in Figure 1 is a Kepler triangle (its sides obey the progression ), or the square pyramid whose height to base ratio equals h:b=4:π like the Great Pyramid of Giza. These last two pyramids approximate very well the Squaring of the Circle.
Pyramids with a regular star polygon as its base are known as star pyramids. Some examples are the pentagrammic and the heptagrammic pyramids shown in Figure 3.
 |
 |
 |
| (a) Pentagrammic | (b) Heptagrammic I | (c) Heptagrammic II |
| Figure 2: Some star pyramids (click on the image to get a 3D view that you can zoom and rotate). | ||
2.- Dipyramids and Prisms
A closely related polyhedron is the dipyramid (or bipyramid), which is formed by joining two pyramids base to base (Figure 3b). This operation hides the original "base" that gives the dipyramid its name. The dipyramids are the dual polyhedra of the uniform prisms, which are right prisms with regular polygonal bases and equal edge lengths (Figure 3a). The following figure shows some dipyramids with their corresponding dual prisms.
|
TRIANGULAR PRISM |
TRIANGULAR DIPYRAMID |
|
CUBE |
OCTAHEDRON |
|
PENTAGONAL PRISM |
PENTAGONAL DIPYRAMID |
|
HEXAGONAL PRISM |
HEXAGONAL DIPYRAMID |
|
OCTAGONAL PRISM |
OCTAGONAL DIPYRAMID |
|
DECAGONAL PRISM |
DECAGONAL DIPYRAMID |
| (a) Uniform prisms | (b) Dipyramids |
| Figure 3: Click on any image to get a 3D view that you can zoom and rotate. | |
3.- Antiprisms and Deltohedrons
An antiprism is a polyhedron composed of two parallel copies of a base polygon connected by an alternating band of triangles (Figure 4a). Antiprisms are similar to prisms except the bases are twisted relative to each other, and the side faces are triangles rather than quadrilaterals. Uniform antiprisms have equilateral triangles as side faces.
The dual polyhedron of an antiprism is a deltohedron (or trapezohedron or antidipyramid). A deltohedron can be decomposed into two equal pyramids and a middle antiprism (Figure 4b). The following figure shows some antiprisms and their corresponding dual deltohedrons.
|
SQUARE ANTIPRISM |
SQUARE DELTOHEDRON |
|
PENTAGONAL ANTIPRISM |
PENTAGONAL DELTOHEDRON |
|
HEXAGONAL ANTIPRISM |
HEXAGONAL DELTOHEDRON |
|
OCTAGONAL ANTIPRISM |
OCTAGONAL DELTOHEDRON |
|
DECAGONAL ANTIPRISM |
DECAGONAL DELTOHEDRON |
| (a) Antiprisms | (b) Deltohedrons |
| Figure 4: Click on any image to get a 3D view that you can zoom and rotate. | |