- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Archimedean Solids

The Archimedean solids are the only 13 polyhedra that are convex, have identical vertices, and their faces are regular polygons (although not equal as in the Platonic solids). Since all the vertices are identical to one another, these solids can be described by indicating which regular polygons meet at a vertex and in what order. For example, the Cuboctahedron has two triangles and two squares meeting at each vertex, alternatively, so is notated as (3,4,3,4).
Five Archimedean solids are derived from the Platonic solids by truncating (cutting off the corners) a percentage less than 1/2. The percentage of truncation f varies in each solid; the objective is to obtain new regular polygons as faces. Its general formula is
where the factor α depends on the shape of the original face: a triangle (Tetrahedron,Octahedron and Icosahedron), a square (Cube), or a pentagon (Dodecahedron) and is given by:
The images below illustrate this first five Archimedean solids. If you click on any of them, you will get a 3D model of the solid which you can freely zoom and rotate:
 |
 |
 |
 |
 |
|
Truncated Tetrahedron (3,6,6) |
Truncated Cube (3,8,8) |
Truncated Octahedron (3,8,8) |
Truncated Icosahedron (5,6,6) |
Truncated Dodecahedron (3,10,10) |
Two special Archimedean solids can be obtained by full truncating (f=1/2) either of two dual Platonic solids: the Cuboctahedron, which comes from trucating either a Cube, or its dual an Octahedron. And the IcosiDodecahedron, which comes from truncating either an Icosahedron, or its dual a Dodecahedron. Hence their "double name":
 |
 |
|
| Cuboctahedron | Icosidodecahedron |
The next two solids, the Truncated Cuboctahedron (also called Great Rhombicuboctahedron) and the Truncated Icosidodecahedron (also called Great Rhombicosidodecahedron) apparently seem to be derived from truncating the two preceding ones. However, it is apparent from the above discussion on the percentage of truncation f that one cannot truncate a solid with unequally shaped faces and end up with regular polygons as faces.
Therefore, these two solids need be constructed with another technique. Actually, the can be built from the original platonic solids by a process called expansion. It consists on separating apart the faces of the original polyhedron with spherical symmetry, up to a point where they can be linked through new faces which are regular polygons. This process is illustrated in the following figure:
 |
 |
|
| Rhombicuboctahedron | Expansion process (from Wikipedia) |
 |
 |
|
| Rhombicosidodecahedron | Expansion process (from Wikipedia) |
The name of the Truncated Cuboctahedron (also called Great Rhombicuboctahedron) and of the Truncated Icosidodecahedron (also called Great Rhombicosidodecahedron) again seem to indicate that they can be derived from truncating the Cuboctahedron and the Icosidodecahedron. But, as reasoned above, this is not possible.
 |
 |
|
| Truncated Cuboctahedron | Truncated Icosidodecahedron |
Finally, there are two special solids which have two chiral (specular symmetric) variations: the Snub Cube and the Snub Dodecahedron. Here we show only one chiral form of each:
 |
 |
|
| Snub Cube | Snub Dodecahedron |
These solids can be constructed as an alternation of another Archimedean solid. This process consists on deleting alternated vertices and creating new triangles at the deleted vertices. The following figure ilustrates this process for the case of the Snub Cube, which starts from the Truncated Cuboctahedron (also called Great Rhombicuboctahedron):
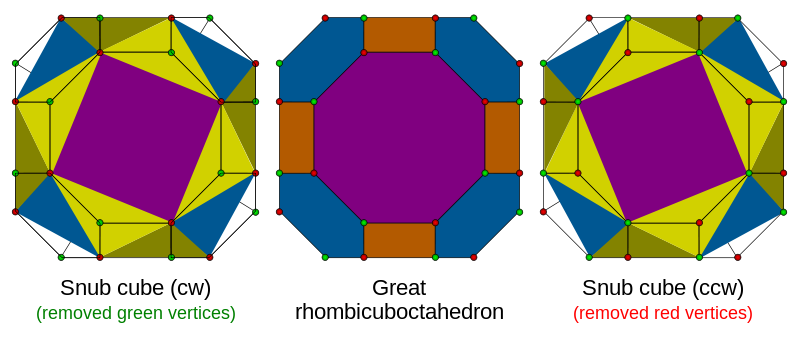
You can find a summarizing table on Archimedean Solids on the article related to Catalan Solids, which are their duals.
