- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Sacred Solids in the Atomic Nucleus
1.- Introduction
"Our picture of the nucleus is so far different from the accepted picture (actually, there is no accepted picture) as to make any comparison impossible. The trained specialist recognizes immediately that if we are right, the whole edifice of 20th Century atomic physics must be rethought, as Dr. Moon had done. Moon was able to make breakthroughs where others could not, in part because he had a hands-on mastery of the crucial experiments on which the theoretical structure was built. He had done the experiments. Few of his peers had the combination of competence and courage to think in the same way.
Laurence Hetch [1]
This article describes a tiny portion of the research conducted by the eminent nuclear physicist Dr. Robert J. Moon (1911-1989) [2], and it also introduces some possible variants of it. I came across Dr. Moon's geometrical model of the atomic nucleus after having known of a nice reorganization of the periodic table of the elements into a tetrahedral structure, the so called Perfect Periodic Table [3]. That made me ask the question: if the atomic elements can be organized in such a way, could the electrons themselves be geometrically organized in a regular way inside the atom? I am certain that there is a positive answer to this question, one that will arrive to us in due course. What it does exist, and nobody usually tells you about it at school, is a nice, coherent, geometrical model of the arrangement of protons in the atomic nucleus, which involves the Platonic Solids.
Up to where modern science knows, every atom of matter is made of positive charged particles -protons- and neutral particles -neutrons- which are known to be concentrated in the atomic nucleus, and of negative charged particles -electrons- which are located around it. It is my firm belief that all those particles work together as an ensemble, but current physics separates the study of the nucleus from that of the extra-nuclear space. At the present, there is no theoretical model capable of describing into detail the structure of the nucleus. Each of the available nuclear models describes some of the known experimental observations, but there is no definite model that explains them all. Dr. Moon's nuclear model accounts for some of the periodicities found in many properties of the atomic elements, and it also explains why some elements -like uranium- may participate in nuclear fission.
In the course of my investigations I rediscovered some alternative interpretations of two widely accepted physical theories: electromagnetism and quantum mechanics. I was surprised to find that, well before James Clerk Maxwell published his famous treatise of electromagnetism -the one which all electrical engineers are taught- Alfred Weber had already proposed a general expression of the electro-dynamical force between moving charged particles. In fact, Maxwell's equations for the electromagnetic field can all be derived from Weber's electrodynamics [4]. The interesting point for the present discussion is that Weber's theory predicts a distance below which the force between two charged particles of equal sign changes from repulsion to attraction [5]. When the modern constants are substituted into his formula one obtains the classical electron radius, despite the fact that Weber developed his theory long before the discovery of the atom!! Therefore, according to Weber's theory, positive charged protons inside the nucleus, instead of repelling, they attract one another.
And why bother about quantum mechanics? Its widely accepted interpretation holds that one can only work with probabilities of finding an atomic particle in a given position inside the atom, and that it does not make sense to talk about the exact position or the trajectory of, say, an electron. Not to mention the possibility that the electron or the proton have an internal structure! Fortunately, a solid alternative interpretation exists according to which making those kind of questions is no longer utter madness. As Weber electrodynamics, it is likely unknown to most physicists. I am talking about De Broglie-Bohm quantum potential. Dr. Moon himself +mentioned in one of his interviews [6] that Louis De Broglie and David Bohm had worked together in the quantum potential interpretation of the Schrödinger equation -also known as pilot-wave theory- until De Broglie's death. This interpretation of quantum mechanics, presented by Louis De Broglie at the 1927 Solvay conference [7], not only predicts exactly all the experimental findings as it does the conventional approach (and some others which it does not explain such as the two slit electron interference experiment or the Aaron-Bohm effect) but it also shows that the probabilistic interpretation of quantum mechanics is a side consequence -not a necessary premise- and that it makes sense to talk about the trajectories and positions of atomic particles!!
2.- On the structure of matter
The following figure shows the modern Periodic Table of the elements. Each element is characterised by its atomic number A, which counts the number of protons (positively charged particles) in its nucleus. This number also indicates the number of electrons (negatively charged particles) that surround the nucleus when the element is in its stable, non-ionized state. Each element is also characterised by its mass number Z, which takes into account the number N of neutrons (neutral particles) in the nucleus. Therefore Z = A + N. Depending on the number of neutrons in their nucleus, some elements have different variants known as isotopes, with the same atomic number but different mass number. Some isotopes are non-stable and rapidly disintegrate. Among the stable isotopes of a given element, the Periodic Table depicts the atomic mass of the most abundant isotope in Nature. The mass number can be generally obtained by rounding the atomic mass to the nearest integer. The highlighted elements in the table will be discussed in next section.
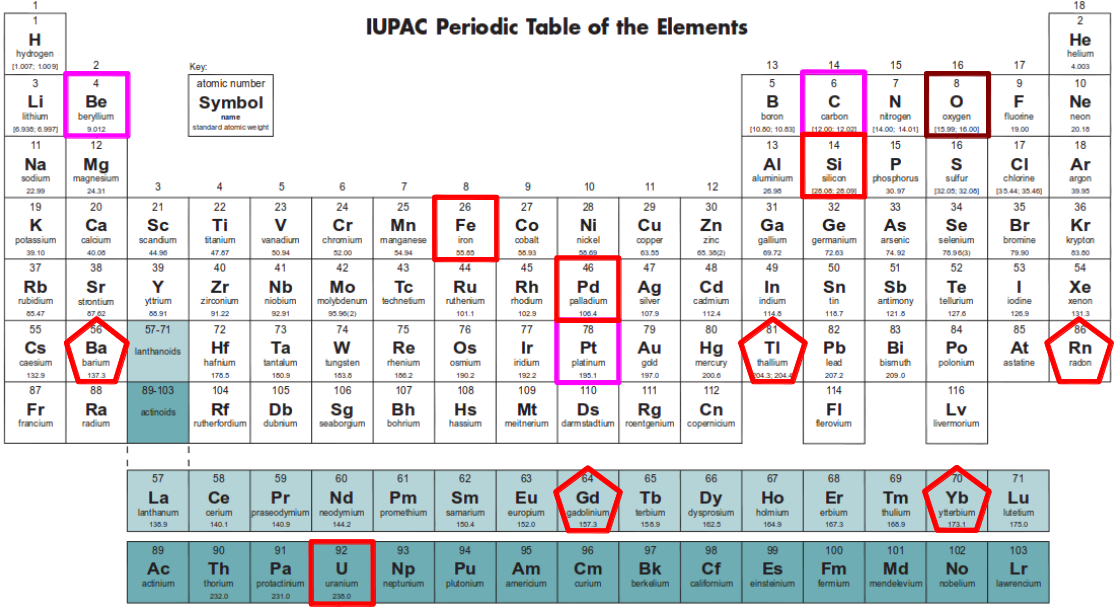
Figure 1: Periodic table of the elements (available here). The elements marked with red squares -either dark or light red- mark the completion of a shell in the first set of four shells in Moon model of the nucleus. Magenta squares mark the elements which I proposed might indicate the closure of additional shells not originally considered by Moon. The elements marked with pentagons mark the completion of each shell in the twin dodecahedral structure of Moon nuclear model.
What can be said about the internal structure of any of those particles? For example, what is an electron? Most physicists agree that it is an entity with the property of a quantum of charge, and that we cannot infer anything about its internal composition from experiments: we are only allowed to talk about the probability of finding an electron somewhere around the nucleus. Fortunately, as mentioned in the introduction, according to the alternative interpretation of quantum mechanics originally suggested by Louis de Broglie in 1927, it does make sense to think of quantum particles as entities with internal structure that can move in some determined -although unknown- trajectories [8]. As to the internal composition of an electron, according to the research conducted by biophysicist Dr. Paulo Correa and his wife, it consists on a quantum of circularized energy in a constant flow that defines a toroidal structure [9]. Dr. Vladimir B. Ginzburg has also developed a simple model of all elementary charged particles in the form of a torus of varying aspect ratio [10].
And what do we know about the internal composition of a proton or a neutron? Physicists don't have a way of looking inside any such particle, but from experiments in particle colliders they agree that a proton (or a neutron) is composed of three more elementary units called quarks. So, in the domain of nuclear physics it appears to make sense to talk about the structure of a particle ha ha ha! In fact, some experiments conducted at the Weizmann Institute of Science have shown that electric current is quantized in units of 1/3 of the quantum of charge [11]. So it is likely that the electron is also composed of some elementary units, but at the moment science does not know this for certain, yet. I suspect that both the proton and the electron have a common internal structure, and they only differ in size and in their internal property of charge. They could well be scaled versions of one another. In fact, physicists hold that beta particles are electrons emitted by the nucleus is the decay process of a neutron in a radioactive element. Similarly, a neutron can be seen as a proton that has "fused" with an electron. But of course in both cases the size of such a nuclear electron must be comparable to that of proton. Therefore, everything seems to point out that electrons in the nucleus are scaled versions of their corresponding extra-nuclear partners! But let's focus on the main topic of the article.
3.- Some properties of the atomic elements
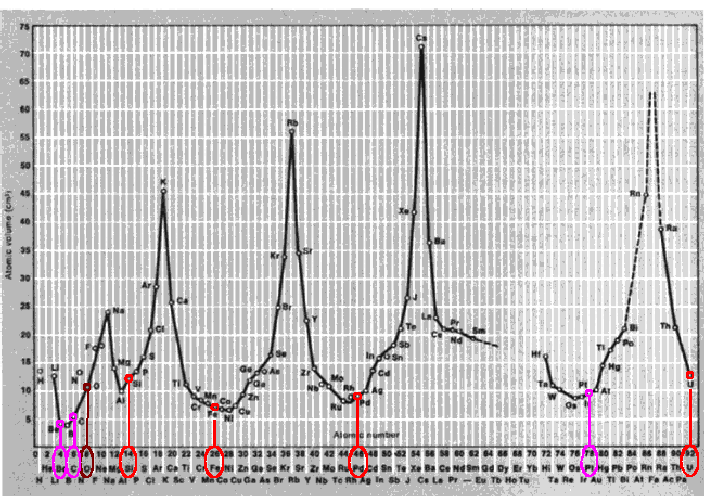
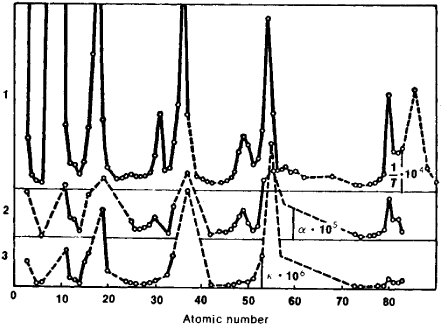
The electrons in the atom are known to be organised in shells, although very little is known about the actual geometric structure of those shells. The noble gases, which are located at the rightmost column in the periodic table (Figure 1), mark the completion of a shell. The leftmost element in next row marks the beginning of a new shell. Several properties, such as the atomic volume, the melting point, the coefficient of linear expansion or the compressibility factor, have a sharp maximum for the atomic number corresponding to the element that starts a new electron shell (3Li, 11Na, 19K, 37Rb, 55Cs). This is graphically shown in Figure 2.
|
(a) |
|
(b) |
|
Figure 2: (a) Dependence of atomic volume on atomic number. (b) Dependence on atomic number of (1) the quantity 104/T, where T is the melting point; (2) coefficient of linear expansion alpha·105; and (3) compressibility factor K·106.(adapted from this reference) |
However, there are some other remarkable points in those graphs, namely their minimum points. Dr. Moon proposes that protons are also organised in shells into the nucleus. As we will show in the following sections, the completion of each of his proposed proton shells nearly corresponds to the atomic elements located at a local minimum of the above properties (4Be, 6C, 8O, 14Si, 26Fe, 46Pd, 92U). I have added two elements at the beginning of the series, Beryllium and Carbon, which were not originally proposed by Moon, but which also correspond to local minima and could easily fit into his model as I will explain later on.
3.- The tetrahedra helix
Before going into detail, let me introduce an analogy that may help us to understand the rationale behind Moon's model. Let's take any game with balls and equal sized rods that can be interconnected together to form polyhedra. We start with a triangle (Figure 3a), and at each step we add a new pack of one ball and three rods (Figure 3b). We can imagine this pack as being a (nuclear) particle that joins a set of already established and organised nuclear particles. The triangle contains three balls and three rods. After adding the first pack, we have four balls and six rods. Are those numbers familiar to you -namely four vertices and six equal sized edges? Of course they can only be organised in three dimensions in the form of a tetrahedron (Figure 3c)! In addition it is the most symmetrical way of organising four elements in three dimensional space, leaving an empty space in the center. I suggest that the four protons of the Beryllium (4Be) nucleus may be organised in such a way. Notice that this element is located near a local minimum of the atomic properties shown in Figure 2.
Let's add a new "particle" (a pack of one ball and three rods). We can put it on top of any of the faces of the original tetrahedron, and we end up with two tetrahedra side by side (Figure 3d). When we add a third additional pack, again we can put it on top of any of the six external tetrahedral faces, ending up with a three tetrahedra bundle shown in Figure 3f. This completes what we will call a turn (because one green rod comes out from every ball in the original triangle starting to define a twist direction). An interesting fact about this set of six balls and twelve equally sized rods is that it can be reorganised in a very symmetrical way, do you guess which one? Yes, it is our familiar octahedron (Figure 3f)!
|
(a) |
(b) |
|
(c) |
(d) |
|
(e) |
(f) |
|
Figure 3: After joining six balls using twelve equal sized rods, the resulting three tetrahedra bundle can be reorganised in the form of an octahedron. If a tetrahedron is taken as one unit of volume, the original bundle was asymmetric and had a volume of three units, whereas the resulting octahedron has a volume of four units and is a perfectly symmetrical distribution of the same set of balls and rods. |
|
You may be wondering: is there any benefit in this reorganisation? Thinking in terms of volume, and supposing that each tetrahedra has one unit of volume, the original bundle had a volume of three, whereas the resulting octahedron has a much large volume of four. We have reached a new structure which, using the same amount of building "material", has the highest symmetry and the largest inner volume possible. Therefore, from this point of view -maximizing volume and symmetry- it is an optimum structure. The final structure also achieves the closest packing of the six elements: an hypothetical circumscribing sphere would have minimum radius in the octahedral, centrally symmetrical structure, than in the three tetrahedra extended one. I suggest that Nature uses this kind of optimization to organise particles in the atom, and in particular protons in the atomic nucleus. If we look at the periodic table of Figure 1, this octahedral organization of six protons could correspond to the nucleus of Carbon (6C) which as Beryllium is also near a local minimum of the atomic properties of Figure 2.
In order to continue adding packs to our structure, now we have two options: either start from the original three tetrahedron bundle, or from the reorganised octahedron. In the first case, each new tetrahedron can be added in a way that continues the twisting direction of what we called the first turn. Figure 4 shows the resulting tetrahedra helix after adding seven packs to the original triangle, and one of its possible symmetrical reorganisations. Had we started from the reorganised octahedron, we could have stellated it adding a tetrahedron to each of its faces. After four such steps, the most symmetrical final structure appears to be a three dimensional tetractis (Figure 4b) or what Buckminster Fuller called a 2-frequency tetrahedron [12]. In addition to being symmetrical, this structure has a volume of eight units instead of the seven units of the ten ball, seven tetrahedra helix shown in Fig.4a (the same amount of "material" can be organised in less symmetrical ways which reach higher volumes, but we leave this as an exercise for the reader).
|
(a) |
(b) |
|
Figure 4: The resulting structure of joining seven tetrahedra to the original blue triangle can be reorganised as a three-dimensional tetractis. |
|
Two more tetrahedra would complete a three turn helix (nine tetrahedra), which happens to contain a total of twelve balls and thirty rods. You may have guessed that these material allows to build an icosahedron, which would have the maximum volume of 18.51 units instead of the 9 units of the original nine tetrahedra helix (Figure 5). Continuing this process we would eventually end up with a final 33 tetrahedra helix. I address the reader interested in an alternative interpretation of this amazing structure to reference [13].
|
Figure 5: A three turn tetrahedra helix contains exactly twelve balls and thirty rods, so it can be optimally organised in the form of a perfectly symmetric icosahedron, which has maximum internal volume. |
If we increase the number of balls up to fourteen, where would we put the two extra balls? One solution, which is not optimum in terms of volume but preserves the previous reorderings, would be to start from the ten ball tetractis of Figure 4 and go on stellating the octahedron until reaching a star tetrahedron (Figure 6). Notice that this structure contains the vertices of a cube (which is held stable by the two big "diagonal" tetrahedra) and those of its dual solid the octahedron. While the inner octahedron could be the spacial distribution of the six protons in a Carbon nucleus, the resulting octahedron+cube structure could well be the distribution of the fourteen protons in the nucleus of Silicon (14Si), which happens to be near another minimum in the atomic properties shown in Figure 2. The picture that has started to emerge so naturally is that of nuclear protons organised into shells: once a given shell is completed (for example the octahedron), protons start filling next shell (the cube), and so on...
|
Figure 6: An eleven tetrahedra helix contains fourteen balls and thirty-six rods that can be reorganised as a stellated octahedron. This is an example of an octahedral shell surrounded by an hexahedral shell. It might reflect the internal structure of protons in the nucleus of Silicon. |
4.- Moon model of the Atomic nucleus
Dr. Robert J. Moon proposed a model of the spatial distribution of nuclear protons that can be understood with the line of thought developed in the previous section. Before going on, I reproduce a dialogue between Fletcher James and Dr. Moon regarding the nature of his model [1]:
"FJ: Dr. Moon, I have a fundamental question about what you are doing in filling in these solids. Are you proposing a structure in which you actually have, quantized within space, a fixed structure, and you have points, particles which are located at rigid fixed intervals from each other within the structure?
RM: No. You have singularities -singularities in space, particle singularities...
FJ: But at fixed, constant distances from each other? or are you proposing that this is occurring in a phase space, and that there is a topological equivalence between this nesting?
RM: Well, no, this is actual space, so there should be a topological equivalent to it. But, this is, these singularities in space may have nothing in them. But they're just a place where these particles can go."
Dr. Moon suggested that the first stable structure to form was a cube whose vertices would define the distribution of the eight protons in the nucleus of Oxigen (8O) (Figure 7a). After adding six more protons, the next shell to complete would be an octahedron. Altogether, they may reflect the symmetric distribution of the fourteen protons in the nucleus of Silicon (14Si). The octahedron and cube form a dual pair, so Dr. Moon placed the vertices of the cube in the midpoints of the faces of the octahedron (Figure 7b). These eight points are all contained in the inscribed sphere of the octahedron. So actually the inner cube structure would be able to move inside the octahedral structure according to the electrodynamic forces acting among the protons. I have offered an alternative distribution of these fourteen protons in Figure 6 (we will return to it in next section). As I mentioned before, Silicon is located near a minimum of the atomic properties shown in Figure 2.
|
(a) |
(b) |
|
Figure 7: (a) The first shell proposed by Moon is a cube, which reflects the distribution of the eight protons in the nucleus of Oxygen. (b) The next shell would form after adding six new protons, reflecting the distribution of the fourteen protons in the nucleus of Silicon. |
|
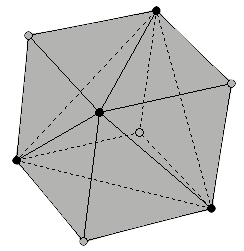
The next proton shell proposed by Dr. Moon is an icosahedron. It is reached after adding twelve new protons to the nucleus of Silicon (Figure 8a). This would lead to the nucleus of Iron (26Fe) totalling twenty-six protons. Iron is also near a minimum of the above mentioned atomic properties of the elements. There are many ways in which an octahedron can be inscribed into an icosahedron. In the first versions of his model, Moon placed the six vertices of the octahedron in the middle of six edges of the icosahedron. Later he proposed to place them onto six icosahedral faces, so that two octahedral and two icosahedral faces become mutually parallel (Figure 8b). Please note that none of those locations of the octahedron inside the icosahedron would allow the former to freely spin. In the following section I will propose an alternative that would solve this problem.
|
(a) |
(b) |
|
Figure 8: (a) The completion of the third shell in the form of an icosahedron reflects the distribution of the twenty-six protons in the nucleus of Iron (26Fe). (b) The vertices of the octahedron are located on six icosahedral faces in such a way that both solids have two mutually parallel faces. |
|
The last shell in this structure, as it could not be another way, would be a dodecahedron (Figure 9). After adding twenty more protons to the nucleus of Iron, we would end up with the distribution of the forty-six protons in the nucleus of Palladium (46Pd). Again, this element falls very near to the next minimum in the atomic properties shown in Figure 2. The icosahedron and the dodecahedron are dual solids, so the vertices of the former would be located in the middle of the faces of the later in a natural way. As the twelve icosahedral vertices are all contained in the inscribed sphere of the dodecahedron, the inner icosahedral structure would be able freely move inside its enveloping dodecahedron.
|
|
|
|
Figure 9: The completion of the fourth shell in the form of a dodecahedron would reflect the distribution of the forty-six protons in the nucleus of Palladium (46Pd). The icosahedral vertices would be able to freely move inside its enveloping dodecahedron. |
|
After completing those four shells, Dr. Moon proposed that the following elements started forming a similar, twin structure on top of one of the dodecahedral faces. Both structures would share the five vertices of that face, as well as the icosahedral vertex located in its middle. So we would be left with just eleven icosahedral and fifteen dodecahedral vertices. Moon hypothesized that the first ten vertices to be occupied by the new protons would belong to the dodecahedron (Figure 10a). They would reflect the distribution of protons in the nucleus of Barium (56Ba). The following eight protons would complete the inner cube giving rise to the nucleus of Gadolinium (64Gd), in the middle of the lanthanide series of elements (Figure 10b). Almost at the end of the lanthanides we find Ytterbium (70Yb), with a completed proton octahedral shell (Figure 10c).
|
(a) |
(b) |
(c) |
|
Figure 10: Moon proposed that the first ten protons of the twin structure occupy ten dodecahedral vertices; the structure reflects the proton distribution in the nucleus of Barium (56Ba), an element which marks the beginning of the Lanthanides. The completion of the inner cube leads to the nucleus of Gadolinium (64Gd), and the completion of the octahedron marks almost the end of the lanthanides at Ytterbium (70Yb). |
||
The next eleven protons would occupy the available vertices of the twin icosahedron, closing another shell and giving rise to the distribution of protons in nucleus of Thallium (81Tl) (Figure 11a). Five more protons close all the shells of the twin dodecahedron, placing us at the noble gas Radon (86Rd) (Figure 11b).
|
(a) |
(b) |
|
Figure 11: (a) The completion of the twin icosahedron leads us to the nucleus of Thallium containing eighty-one protons. (b) The last five protons complete the twin dodecahedral structure which reflects the eighty-six protons in the nucleus of the noble gas Radon. |
|
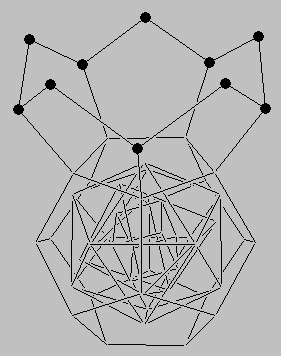
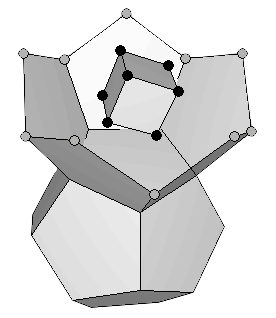
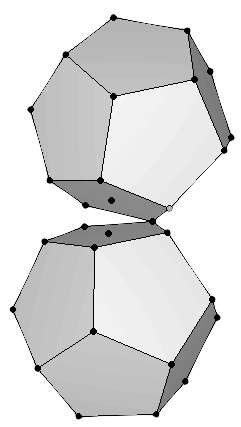
In order to allow new protons into this structure, Dr. Moon proposed that the two dodecahedra could separate as if they were hanging on a hinge (Figure 12a). That would free four spaces that could be occupied by four more protons. Two of the four corresponding elements, Francium (87Fr) and Actinium (89Ac) are not found in nature, because their nucleus is unstable and does not last very long. They have been made in nuclear reactors by bombarding elements with neutrons. To leave room for the additional nuclear proton of the next element, Protactinium (91Pa), Dr. Moon proposed that the hinge breaks and the twin structures are held together at one single point (Figure 12b).
|
(a) |
(b) |
|
Figure 12: (a) To allow the next protons to find their places, the twin dodecahedra must open up, using one edge of the binding face as if it were a hinge. This makes room for four new elements, mostly unstable (b) Next proton can be added if the hinge breaks and the structures are held together by a single proton. |
|
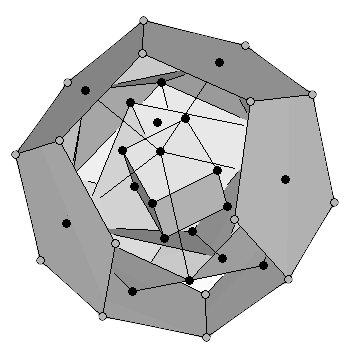
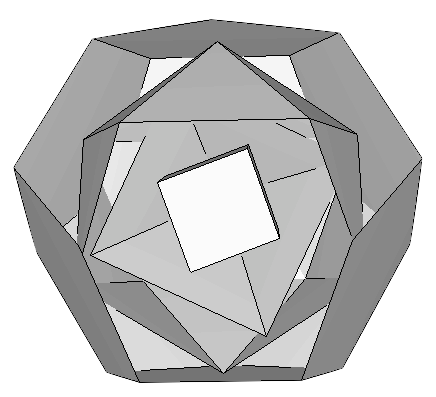
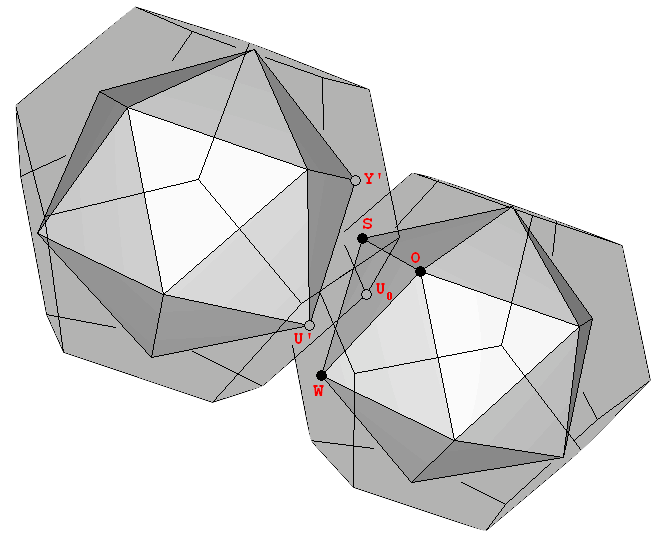
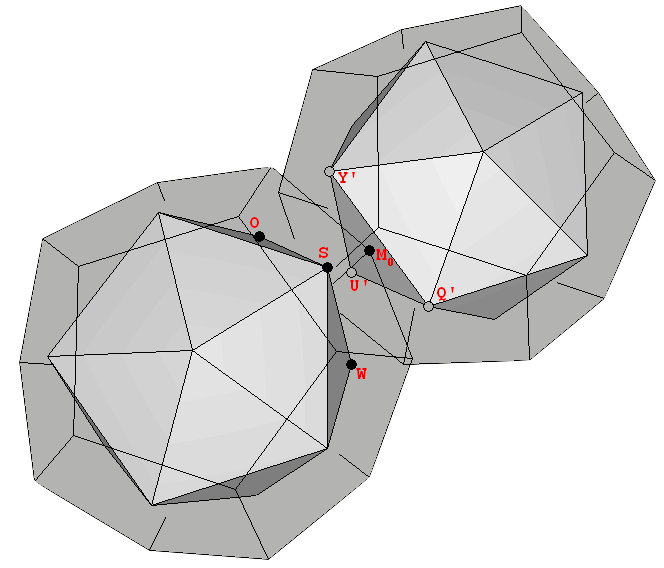
The construction of Uranium (92U) requires that the last proton be placed at the point of joining. This can be accomplished if the structure breaks, and one solid is slightly displaced to penetrate the other (Figure 13). The exact interpenetration of the structure shown in this figure was proposed by Laurence Hetch, after defining a spin axis that will be explained in next section. The resulting structure, quoting Dr. Moon, "is something that's ready for fission [...] if you try to put more neutrons in there, it's going to fiss" [1]. Dr. Robert J. Moon was one of the scientists who first made fission happen in a wartime laboratory on the University of Chicago football field [14].
|
|
|
|
Figure 13: Two views of the twin inter penetrating structures. The exact placement of one vertex of each dodecahedron in the midpoint of each of the opposite icosahedral faces explains the exact number and disposition of neutrons proposed by Laurence Hetch (see next section). |
|
5.- Discussion
The Axis of the Universe
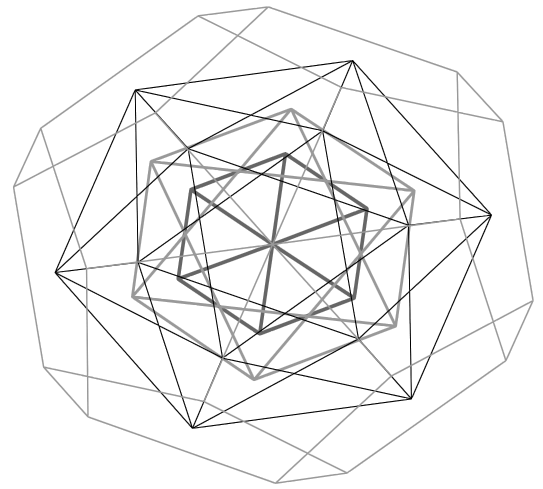
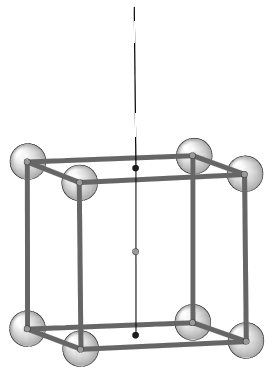
Since the original conception of the model by Dr. Moon, Laurence Hetch and his co-workers have been trying to develop it further. One interesting thing about Hetch proposals is the possible existence of a preferred axis of spin for the atomic nucleus. He suggests that this axis -called the Axis of the Universe- should be perpendicular to the mutually parallel octahedral and icosahedral faces shown in Figure 8. In this way the angular momentum of the protons around this axis would be minimum in some of the shells, such as the cubic one (Figure 14). The reader further interested in the implications of this axis for the nuclear arrangement of protons as well as for the magnetic properties of the elements is addressed to reference [1].
|
|
 |
 |
|
|
Figure 14: Top view of the Moon model from the Axis of the Universe proposed by L. Hetch. Note that the axis is diagonal to to the cube and dodecahedron, but not to the icosahedron nor the octahedron. |
|||
Free spin of each shell
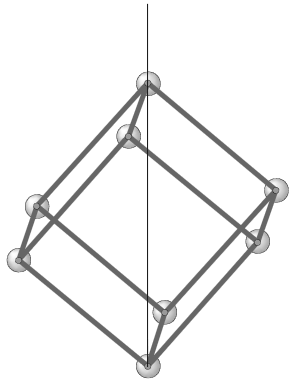
The vertices of the icosahedron, though originally placed at the center of the dodecahedral faces, need not be there at all. In fact the whole icosahedral structure would be able to freely spin inside the dodecahedral structure, in order to align itself in the best way with respect to the preferred axis of rotation. However, that would not be the case of the octahedral structure, because in the original Moon model its vertices surpass the icosahedron inscribed sphere (Figure 15a). I suggest to overcome this limitation by reducing the distance of the octahedral vertices to the center of the structure -and that of the cube vertices proportionally- so that the circumscribed sphere of the octahedron coincides with the inscribed sphere of the icosahedron (Figure 15b). With this simple adjustment, all four shells would be able to spin one inside another, obviously constrained by the electrodynamic forces among their protons.
|
(a) |
(b) |
|
|
Figure 15: (a) The circumscribed sphere of the octahedron in Moon original model is bigger than the inscribed sphere of the icosahedron. (b) Slightly approaching the octahedral vertices to the origin would make both spheres coincident and would allow the octahedron to freely spin inside the icosahedron. |
||
Is the octahedral shell first?
The order of filling of the first two shells -hexahedral and octahedral- is worth a bit more of discussion. The attentive reader may have noticed that the element Oxygen (8O), whose nuclear protons are organised in the form of a cube according to Moon model, is not a minimum of the atomic properties shown in Figure 2. I suggest that this fact is easily explained by an alternative filling order the first two shells. As I commented in Section 3, the first four protons of the nucleus are likely to be organised in the form of a tetrahedron. That would correspond to the nucleus of Beryllium (4Be), which is near the first minimum of the aforementioned atomic properties. The next proton (the fifth) would have no definite place to occupy, but when the number of six protons is reached, it is likely that the ensemble reorganises itself in the form of an octahedron, and that would correspond to the nucleus of Carbon (6C). This element is also close to a minimum of the atomic properties shown in Figure 2, much closer that Oxygen is. The next pronounced minimum appears at Silicon (14Si), which as already mentioned would complete a cube and its dual the octahedron. Which one is inside the other is not clear. Dr. Moon proposed that the cube goes inside, but as I have just argued it could well be the other way round.
What about neutrons?
The atomic nucleus not only consists of positively charged protons; it also contains neutral particles, the neutrons. Moon model does not explain the location of neutrons inside the nucleus. In fact, Dr. Moon used to say: "the protons find their parking place at what would correspond to the vertices. And then the neutrons, which are also out there, we’re not going to worry about them, because they have no charge and they can be most any place" [6]. However, Larry Hetch has also worked on this topic and he essentially proposes that neutrons can occupy the midpoints of the edges of the nested platonic solids, as well as the center of the icosahedral faces not already occupied by protons [13]. The nucleus of Uranium-238 provides a striking evidence in support of his proposal. We have seen that in the Uranium nucleus the two dodecahedral structures interpenetrate one another. The number of edges and face centres left for the neutrons to occupy are:
| Cube faces | 6 |
| Cube edges | 12 |
| Octahedral edges | 12 |
| Icosahedral edges | 30 |
| Icosahedral faces | 13 |
| TOTAL | 73 |
That would leave 73 neutron positions on each twin structure, precisely the correct number for the 146 neutrons of Uranium-238!! In addition, it should be noticed that my proposed reordering of the shell filling would not alter this count, because the two additional faces of each icosahedron occupied with by two extra vertices of the cube would be compensated by the two extra octahedral faces in the innermost shell, so the total would be the same:
| Octahedral faces | 8 |
| Octahedral edges | 12 |
| Cube edges | 12 |
| Icosahedral edges | 30 |
| Icosahedral faces | 11 |
| TOTAL | 73 |
Last update: 2013/03/21
REFERENCES
[1] Hetch L., Stevens Ch.B.: "New Explorations with The Moon Model" ,2004.
[2] Hetch L.: "Who was Robert J. Moon?" ,2000.
[3] Tsimmerman V.: "Perfect Periodic Table".
[4] Assis A.K.T., TorresSilva, H.: "Comparison between Weber's electrodynamics and classical electrodynamics".
[5] Hetch L.: "The Atomic Science textbooks don't teach" ,1996.
[6] Hetch L.: "The Life and Work of Dr. Robert J. Moon" ,2004.
[7] Bacciagaluppi G., Valentini A..: "Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference".
[8] Bohm D., Hiley B.J., Kaloyerou P.N.: "An Ontological basis for the Quantum Theory".
[9] Correa P.N., Correa A.N.: "The Electric Aether and the Structure of the Electron".
[10] Ginzburg V.B., "Three-Dimensional Spiral String Theory".
[11] De-Picciotto R. et al., "Direct observation of a fractional charge".
[12] Edmondson A.C., "A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller" ,2007.
[13] Kappraff J., "The Flame-Hand letters of the Hebrew Alphabet" ,2002.
[14] Hetch L.: "The Geometric Basis for the Periodicity of the Elements" ,1988.