- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Phi in Atomic Structure
1.- Introduction
In this article we will show that the Golden Ratio provides a quantitative link between various known quantities in atomic physics. Most of it is based on the extensive research of Dr. Rajalakshmi Heyrovska. The interested reader will find a summary of her research in this book chapter entitled "The Golden ratio in the creations of Nature arises in the architecture of atoms and ions".
While searching for the exact values of ionic radii and for the significance of the ionization potential of hydrogen, Dr. Heyrovska has found that the Bohr radius can be divided into two Golden sections pertaining to the electron and proton. More generally, it was found that is also the ratio of anionic to cationic radii of any atom, their sum being the covalent bond length. After that she showed, among other facts, that many bond lengths in organic and inorganic molecules behave additively, and are the sum of the covalent and/or the ionic radii, whether partially or fully ionic or covalent. In addition, a new interpretation and a very accurate value of the fine structure constant has been discovered in terms of the Golden Angle.
2.- The Golden Ratio, Bohr radius and the ground state energy of Hydrogen
The ground state Bohr radius of atomic hydrogen, , is defined as
where is the electron charge, is the permittivity of the vacuum, is the ground state energy and is the ionization potential of hydrogen. Recently, the bonding radius of hydrogen with carbon has been shown to be by density functional methods. This has motivated the discovery by Dr. Heyrovska [1] that , the distance between the electron and the proton , can be divided at the point of charge neutrality into two Golden sections as follows:
where . Figure 1 illustrates this division (plus some more points to be explained below) showing a circle of radius around the electron , a circle of radius around the proton , and a circle of radius containing both of them:
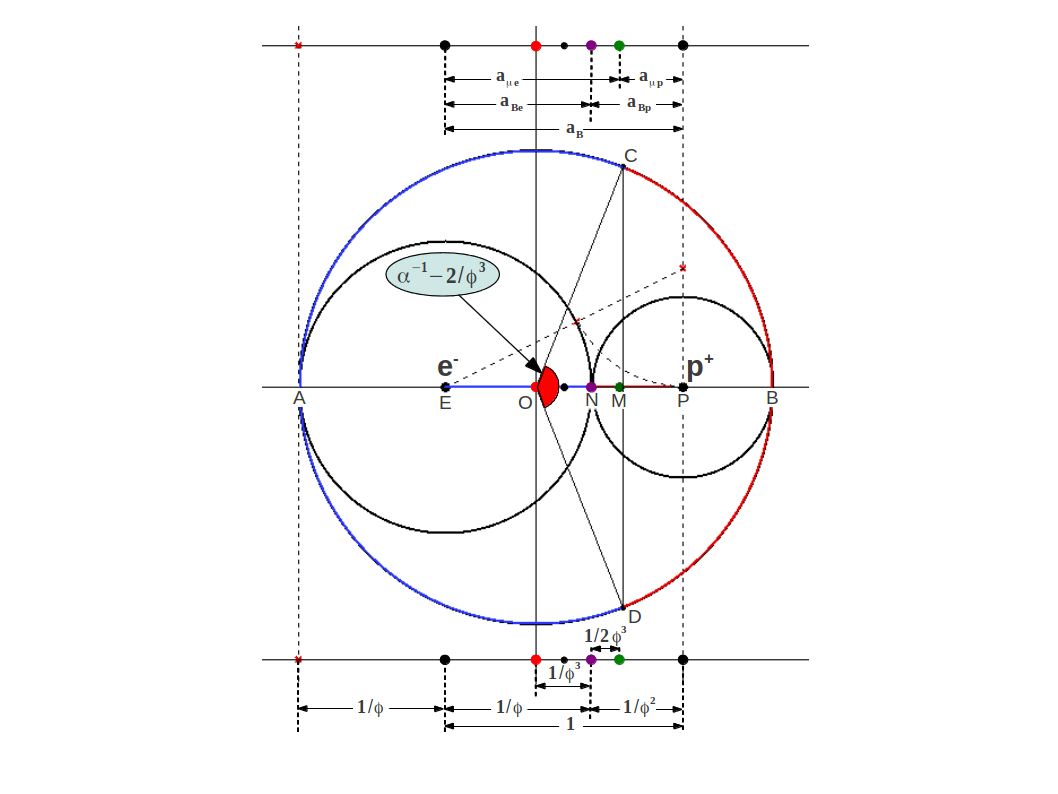 |
| Figure 1: The Bohr radius of the hydrogen atom is divided into Golden sections and at the point of electrical neutrality N, as the auxiliar right angle triangle makes clear. The magnetic center is located at point M, at a distance from the electrical neutrality point towards the proton. The circumference of the outer circle is also divided into two golden arcs CAD and CBD by means of the Golden angle. Note that each arc length equals the perimeter of the inner circumferences. The shorter arc is closely related to the Fine Structure constant, whose value is very near the Golden Angle shown in red. In addition, the chord CD intersects the horizontal very near the magnetic center M. |
The fact that the Bohr radius is divided into Golden sections provides it with the property (not evident at first sight) that
This shows that the ground state energy of the hydrogen atom itself can be expressed as the difference of two terms:
3.- The Golden Ratio and the g-factors
The g-factors of the electron and the proton ( and respectively) are measures of the anomalies of their magnetic moment. They are also related to the Golden Ratio as follows:
where
This shows that the magnetic center of the hydrogen atom (point M in Fig.1) is shifted from the point of charge neutrality towards the proton by an amount (see Fig.1).
The preceding equations imply that
or equivalently that
4.- The Golden Ratio and the bond length of diatomic molecules
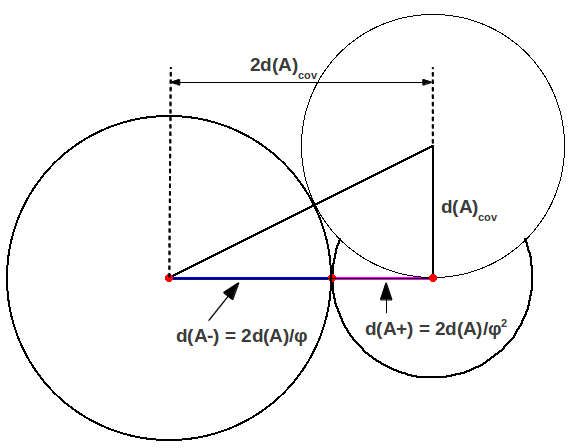
In general, the length d(AA)=2d(A) of any covalent bond AA can also be considered as the sum of two Golden components d(A+) and d(A-) given by
where
and
These correspond to the radii, or actually anionic and cationic bond lengths. This is ilustrated in Figure 2, where you can see that the Bohr radius is the side of a square whose diagonal is . Figure 3 shows the particular case of hydrogen, the simplest diatomic molecule.
 |
|
| Figure 2: Golden division of a general covalent bond. |
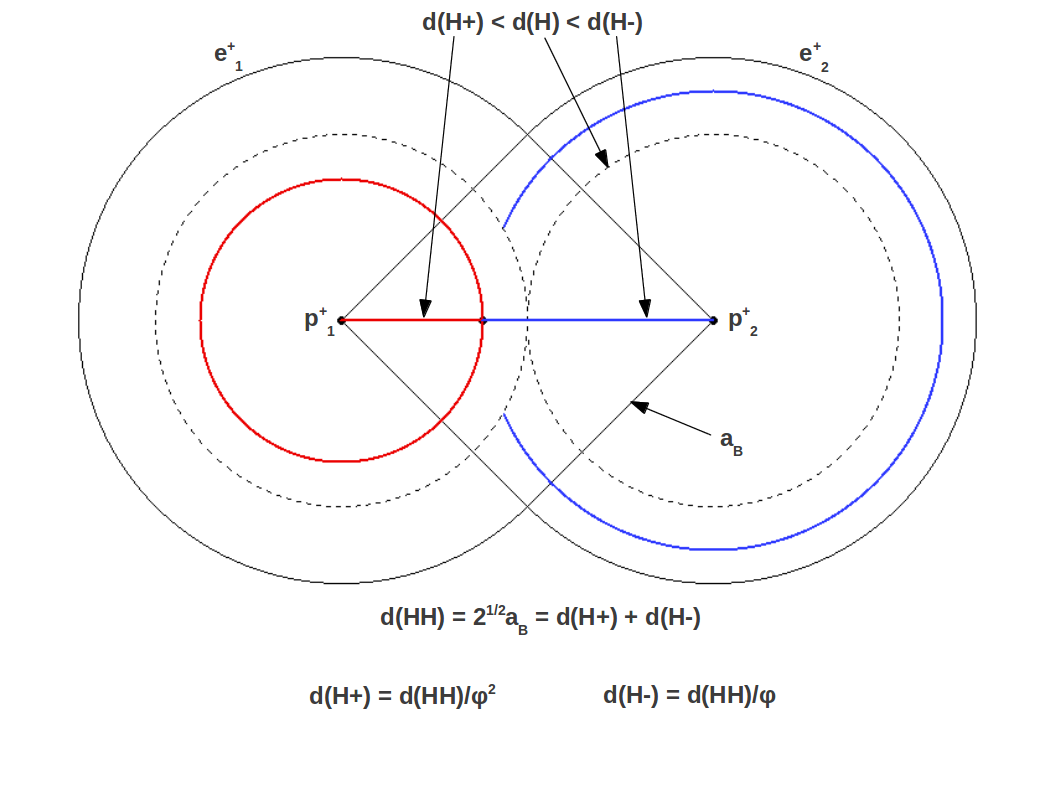 |
| Figure 3: Golden division of the covalent bond in the Hydrogen molecule |
This theory can be extended even to bond lengths between dissimilar atoms. Figure 4 shows a very close agreement between the measured bonds of several compounds and the calculated values as the sums of both covalent or one covalent and the other ionic, or both ionic radii (see table 3 in [1]):
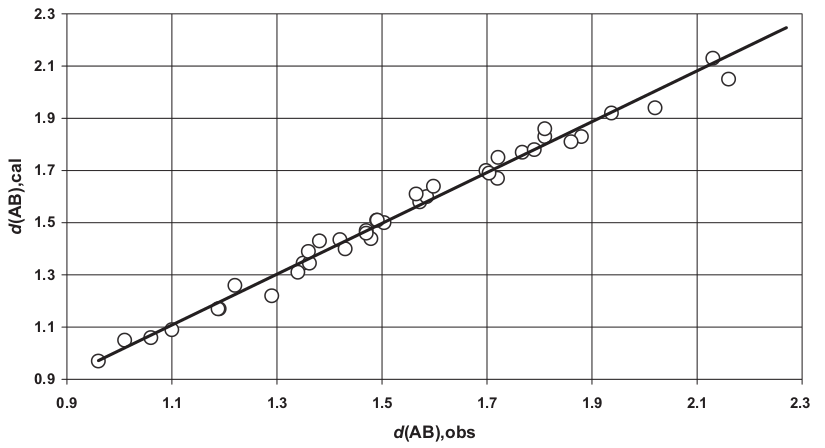 |
| Figure 4: Very good agreement between the calculated sum of bonding distances d(AB),cal and the observed values d(AB),obs. All values in Amastrongs [1]. |
5.- The Golden Ratio and the Fine Structure constant
Ever since Sommerfeld introduced the fine-structure constant into physics, it has puzzled many scientists like Eddington, Dirac and others. Quoting Feynman [2]: “ ... is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the "hand of God" wrote that number, ..." The constancy (or not) of α defined as
where , , h and c are respectively, the charge, electric permittivity of free space, Planck’s constant and the speed of electromagnetic waves in vacuum, is still being debated.
Dr. Heyrovska proposed another interpretation of α based on the observation that it is close to the Golden Angle. In Figure 1 you can observe that the outer circle has been divided into Golden arcs, which are (red portion) and (blue portion). The small part corresponds to the Golden Angle shown in red in the center.
The Fine Structure constant equals this angle plus a small correction that can be stated in two different ways. In the direct way, the correction factor is
where is related to the advance of perihelion in Sommerfeld's theory [3] and γ is the relativity factor
But in the inverse way, the Fine Structure constant can also be formulated for the first time exclusively in terms of the Golden Ratio as follows:
therefore
which agrees with CODATA value with an error as small as
References
[1] Heyrovska R., "The Golden ratio, ionic and atomic radii and bond lengths", Molecular Physics, 103, pp.877-882.
[2] Tomonaga S-I., Schwinger J. and Feynman R. P.,http://nobelprize.org/physics/laureates/1965/
[3] Ruark A.E., Urey H.C., "Atoms, molecules and quanta", Volume 1, Dover Publications, New York, 1964, p.134.
