- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
On the concert pitch A=432 and c=128
Last updated:
01/09/2013
Table of Contents
1.- Introduction
2.- Comparing the scales in concert pitch A=440 and A=432
3.- Experiments with individual tone frequencies
4.- Tuning frequencies for the Greek Aulos Modes
5.- On the hidden qualities of a tone
6.- References
1.- Introduction
In the first part of this article the structure of modern and ancient musical scales was described in detail. Scales were compared, and we reported some aural or qualitative differences in the sound of similar intervals from different scales. Scales define the intervals between frequencies of all the notes in an octave. The frequency of every note is usually given in a normalized way: it is referenced to the frequency of the first note, called the tonic. Once the frequency of a note is fixed, the frequencies of the remaining notes in the scale become also fixed, according to the relative intervals given by the structure of the scale.
Modern instruments are tuned by fixing not the tonic, but the sixth note in the scale to a frequency or concert pitch A=440Hz. In last section, we explained the practical findings of musician researcher Maria Renold when playing music in her new scale of twelve fifths. She reiteratively observed that the intervals and tones become antisocial, and indeed cause people to provoke one another when the concert pitch A=440Hz is used. On the other hand, intervals and tones have a beautiful, pleasant and harmonic effect on the human being when tuned to A=432Hz. The comparison was made over many years and in many places, and the same phenomena always took place. These findings show that tones of certain frequencies hide characteristic qualities which can have major effects on human beings.
To rule out the possibility that this behavior was only found in her particular scale, she conducted a series of aural experiments on more than 2000 people on several countries comparing a pair of individual tones obtained from both tuning methods (A=440Hz and A=432Hz). This way she eliminated the influence of the interval structure of any scale. The results were astonishing: almost all of the people found unmistakably and individually different qualities between tones representing the same musical note in the two tuning methods. Over 90% of people found that the tones from the A=440Hz tuning method sounded uncomfortable, irritating and unpleasant, whereas the tones obtained from the A=432Hz tuning method sounded peaceful, pleasant and full. Many comparisons with the same results were made using different instruments, so the individual quality of the tones originates in the tones themselves and not in the instruments on which they are played. Independently of this author, several musicians and teachers have made similar observations. Another key point is to play them on a non-electrical instrument: Maria Renold observed that otherwise the inherent qualities of a tone are lost. Further details are given later in this article. We shall also present the recommended tuning frequencies for the Greek Aulos Modes. Finally, we discuss on the possible origin of the hidden qualities of tones that human beings are able to perceive but not yet to measure.
2.- Comparing scales in concert pitch A=440 and A=432
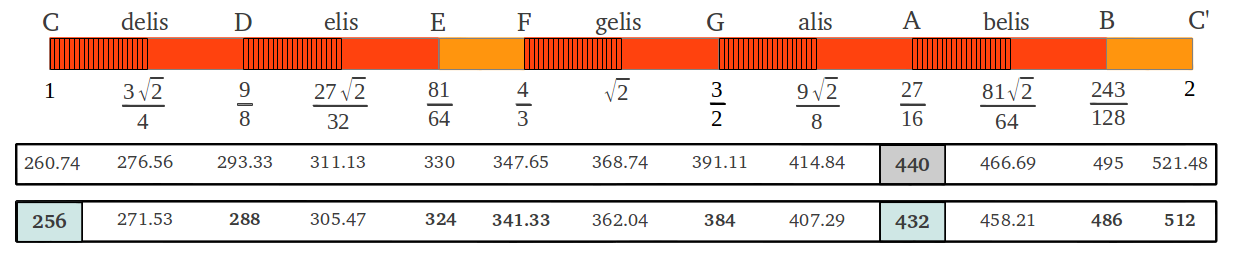
The tone frequencies of the Equal Temperament Scale are shown in Figure 1 for several values of the concert pitch. Here we can clearly appreciate that the structure of the scale -namely the length of its intervals- is preserved, whereas the frequencies of the individual tones are different in each tuning method. The frequencies of the tones at A=440Hz are very different from those at A=432Hz. Tuning at C=256Hz (a higher octave of 'Philosopher's c=128Hz') provides very similar but not the same frequencies as tuning at A=432Hz in the Equal Temperament Scale. On the other hand, those two tuning methods coincide in the scale of Twelve Fifths (Figure 1b) because this scale contains the true intervals of the diatonic Aristoxenus Greek scale.
|
|
|
|
|
|
| Figure 1: Tone frequencies (in Hz) of (a) the Equal Temperament Scale and (b) the Scale of Twelve Fifths for concert pitch A=440Hz, A=432Hz and c=128Hz. |
It is also interesting to notice that, for a given tuning method, the frequency of any particular note is very similar in the Equal Temperament Scale and in the Scale of Twelve Fifths. Therefore, if you are a piano player but you don't want to switch to Maria Renold's scale, you can give the concert pitch A=432Hz a try by simply retuning your piano to this concert pitch without the need of changing the scale. Maria Renold reports on "a lady who had taught the piano for many years and had been an opera singer; she had tuned her piano to C=256Hz for over 20 years and she had found that with this tuning pitch her vocal talent, which through age or incorrect singing had lost its natural elasticity, soon became pliant again and regained its useful freshness". According to her, "tuning to c=128Hz makes it possible for the human organism to balance out different types of existing disharmonies better and more quickly. A voice schooled in this way can easily adapt to and master the problems connected with public singing and present day tensed tuning" [1, p.79].
Table 1 compares the frequencies of the individual tones using the three tuning methods, in the previous two scales as well as in the Just Intervals Scale.
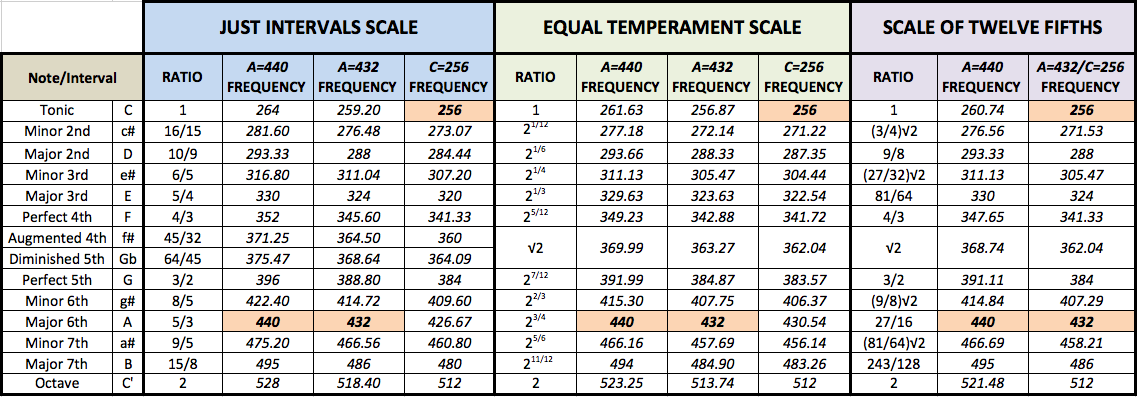 |
|
| Table 1 |
3.- Experiments with individual tone frequencies
Maria Renold conducted very simple experiments, limited to two pairs of tones based on the concert pitches c=128Hz/A=432Hz and A=440Hz and their octaves. The frequencies of the two pairs of tones were as follows [1, p.74]:
(1) c = 128.000 Hz and c = 130.813 Hz (located a lower octave of C = 256.000 Hz and C = 261.626 Hz, see Table 1)
(2) a1=108.000 Hz and a1 = 110.000 Hz (located two octaves below A = 432.000 Hz and A = 440.000 Hz, see Table 1)
Aural experiments were carried out with these two pairs of tones on more than 2000 people of all ages and different occupations in the USA, Italy, Germany and Switzerland, and the results were recorded. Efforts were made to create an atmosphere as natural and unconstrained as possible. The listener were told that the frequency of the tones was not important, but that we were concerned with the character of each one. The tones were played one after the other as required, and the sequence was varied. The cardinal question was: do the two tones in each pair have a different effect, although their difference in frequency is minimal?
Quoting Maria Renold "the results were extraordinarily interesting and unequivocal. Almost all of the people questioned said that the two pairs of tones and their octaves had unmistakably and individually different qualities for them as listeners. It was not easy to put these qualities into words as the experience was new and unexpected [...] Over the course of the years many comparisons of this type were made, using [the monochord and], for example, home made bamboo flutes, student violins and concert instruments, with the tones played on the better instrument and then on the less good instrument. The result was always the same, with each tone proving to have an inherent quality and this quality remained constant, no matter in which register or on what instrument it was played. We may therefore stipulate that the individual quality of the tones originates in the tones themselves and not in the instruments in which they are played" [1, p.74].
After having established that the chosen tones have definite inherent qualities, it was attempted, in spite of the expected difficulties, to find out from the listeners more exactly what the aural impressions of the pairs of tones were. The participants were asked which of the two tones in each pair they preferred. Their answers were surprising: "Although a1=110Hz (440Hz) was the more familiar tone, only 3-8% of participants preferred it; c = 130.828 Hz (261.656Hz) was preferred by even fewer. In other words, over 90% of listeners preferred c = 128 Hz and a1 = 108 Hz (the lower octave of A=432Hz)" [1, p.76].
The listeners were then asked to give the reason for their preference. The tones were played again as often as required. As explained previously, all these experiments were made over the course of 20 years and with many people. Here we report a brief summary of the collected answers [1, p.76-77]:
|
Percentage |
a = 220 Hz (and a1 = 110 Hz) | a = 216 Hz (and a1 = 108 Hz) |
|---|---|---|
| 3-8% |
- sounded beautiful |
- sounded impersonal |
| over 90% |
- sounded uncomfortable |
- sounded correct and complete |
|
Percentage |
C = 261.565 Hz (and c = 130.828 Hz) | C = 256 Hz (and c = 128 Hz) |
|---|---|---|
| 3-8% |
- sounded happy |
- stimulated questions - had an unsettling effect |
| over 90% |
- sounded biting |
- belonged to the human being |
Some detailed accounts given by teachers and musicians who had developed a more conscious attitude to music are the following [1, p.78]:
- "Independently of each other, an elderly violinist and teacher, a young student and a therapist immediately realized that A = 432 Hz was the tone to which they habitually tuned their instruments when they payed on their own.
- A concert violist who until then had used the customary concert pitch had often noticed when teaching adults and children that many tended to suffer from nervousness and lack of concentration. He therefore tuned all instruments, including his own, to c = 128 Hz and A = 432 Hz. The result was that a lot of the nervousness disappeared and that the students were able to make music in greater harmony.
- A two year old boy (not yet a musician or teacher) who was able to walk but not yet to talk and was present at one such aural experimentation, sat peacefully and happily with a clear glaze beside his parents while the tones c = 128 Hz and C = 256 Hz, a1 = 108 Hz and a = 216 Hz were played. When a1 = 110 Hz and a = 220 Hz, and c = 130.813 Hz and C = 261.626 Hz were played, he displayed definite discomfort, getting more and more restless and finally protesting against these tones by stomping loudly around the room.
- Two curative teachers were familiar with the concert pitch A = 440 Hz. Having taken part in the experiments and heard the tones a1 = 108 Hz and a = 216 Hz, and c = 128 Hz and C = 256 Hz they were so shocked by the goading quality of a1 = 110 Hz and a = 220 Hz that they resolved from then on to tune their instruments to c = 128 Hz".
Independent of Maria Renold, several musicians and teachers have made similar observations. Their findings agree with her own and show that they arise from the phenomena themselves and are not caused by conscious or unconscious influence from the author. Besides the piano teacher and opera singer cited in the previous section, there is also the case of an English curative teacher. She did a lot of unaccompanied singing with about 400 children and adolescents, and she noticed that all of his pupils managed the melodies without difficulty and returned correctly to the beginning tone when it was C = 256 Hz, which was by no means the case when the tone was A = 440 Hz [1, p.79].
A personal judgment of the inherent qualities of individual tones that have been described can only be done by hearing them and letting them work on oneself, but it is very important that they be played on a non-electrical instrument. All experiments that Maria Renold conducted with electronically produced tones failed. The tones produced even by the highest quality machines, no matter at which frequency, "all had the same leveling quality, and indeed a quality of yawning emptiness. It would be wrong, however, to draw the conclusion from this that electronic tones are easier for human beings because they eliminate the individual quality of tones. On the contrary, electricity puts its its own quality on tones, and this is always there whether the sound is reproduced electronically or even merely amplified. It can be metaphorically described as a grinding vacuum" [1, p.73]. In a set of experiments in which the tones were recorded from live instruments and replayed with high quality equipment, "a shadow of the tone qualities could be sensed, though not the qualities themselves". However, those observations should not preclude us to experiencing electronically reproduced music at a new concert pitch A = 432 Hz or C = 256 Hz. As an example, a close friend of mine has experienced a great improvement in the inherent qualities of several musical pieces -especially opera- originally produced at A = 440 Hz, after converting them to A = 432 Hz.
4.- Tuning frequencies for the Greek Aulos Modes
In the previous article, we have shown the rich interval structure of the seven ancient musical scales known as the Greek Aulos Modes, which were the musical scales actually studied in the Pythagorean school. However, nothing was said about the tuning frequency of those scales. According to Maria Renold, "to allow modern human beings to work safely with the modes, it is necessary that, as well as taking care with the intonation of intervals, attention is also paid to the pitch of the single scale degrees. The modes have a very powerful effect and work into the human physical and rhythmical organization. This was already observed by [his rediscoverer] Kathleen Schlesinger" [1, p.85].
Miss Schlesinger tuned the modes using the fundamental frequency c = 128 Hz. If we are playing the modes in a monochord, this is the frequency obtained when the whole string length is used. With this constraint, there are still two ways of tuning the modes. The first alternative, the one actually used by Schlesinger, is to divide the string length in a different number of segments for each selected mode: 22 segments for the Sun mode, 24 for the Venus mode, etc. (see Figure 36 in the previous article). In this way, all the modes share the same tonic frequency (128 Hz) but the generic reference frequency or Arché -given by the length of the smallest interval- is different for each mode (Figure 2). For example, the generic frequency of the Sun mode would be 128·22 = 2816 Hz and the generic frequency of the Venus mode would be 128·24 = 3072 Hz.
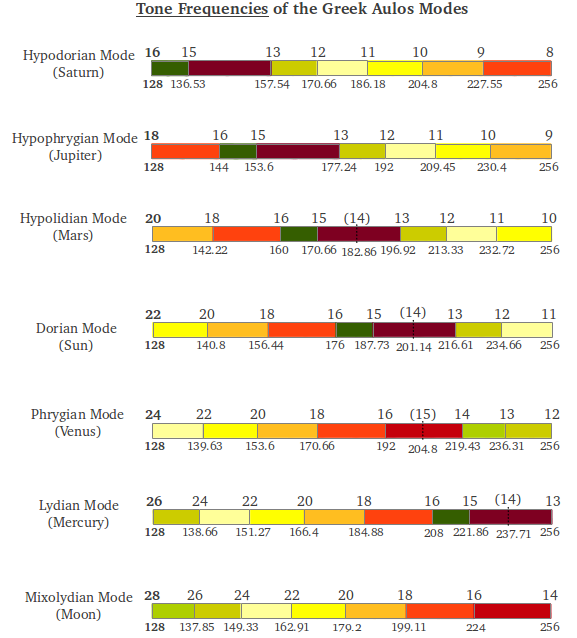 |
|
| Figure 2: Tone frequencies (in Hz) for tuning the Greek Aulos Modes by adjusting the string for a fundamental frequency c=128Hz and using a different number of string divisions for each mode. |
The other alternative for tuning the seven modes from a string fundamental c = 128 Hz is as subspecies of a common mode. As shown in Figure 3, if we divide the string length into 32 segments, the generic frequency will be 128·32 = 4096 Hz. Then each mode is played by sliding to a different octave. With this method, the tonic frequency is different for each mode (186.18 Hz for the Sun mode, 170.67 Hz for the Venus mode, etc.) but all the modes share the same mese (256 Hz).
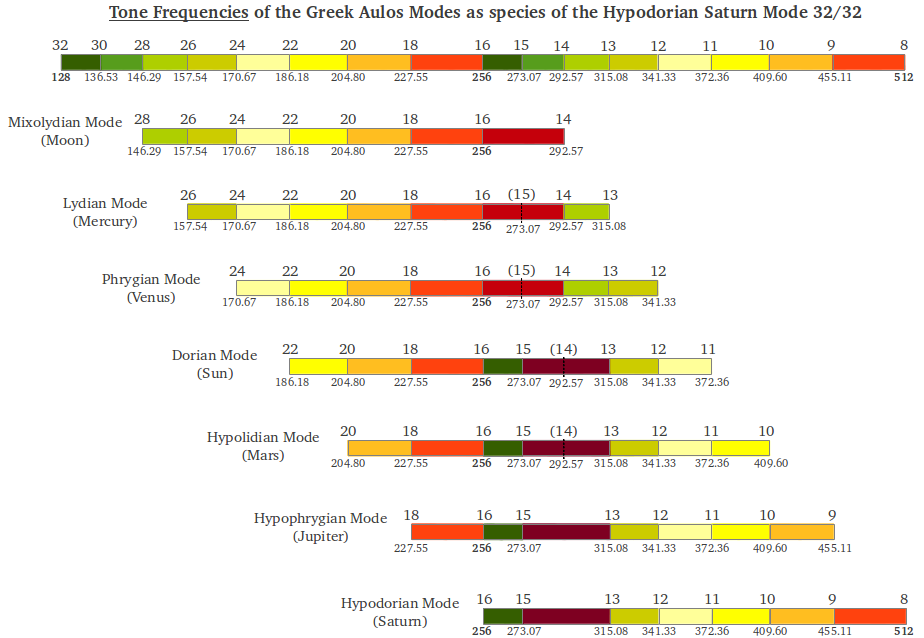 |
|
| Figure 3: Tone frequencies (in Hz) for tuning the Greek Aulos Modes as subspecies, by adjusting the string for a fundamental frequency c=128Hz and dividing it into a fixed number of segments. Then each mode is played by sliding to a different octave. |
It is very informative to observe how the two methods of tuning the modes influence modern people. Maria Renold reports that years of observation have led to the following [1, p.85]: "If one tunes the modes to the fundamental c = 128 Hz and mese = 176 Hz [in the Sun mode, see Figure 2] as Schlesinger did, this creates a kind of ecstasy amongst listeners and a degree of somnambulance on extended listening. [On the other hand] no effect on the mind of modern-day listeners has been observed with the Sun mode tuned to the mese c = 128 Hz or C = 256 Hz and the fundamental to 186.182 Hz, i.e. the generic tone on c5 = 4096 Hz. This method of tuning actually leaves listeners totally free, letting them handle music and configure the mode in a completely free way. This second method of tuning [...] seems more suitable for our time".
According to Figure 3, it would seem that with the second method all the modes should share their qualities with the generating Saturn mode from which they have been derived. But "on hearing [the Sun mode tuned this way], one immediately realizes that this is not the case, however, for one experiences such a mode as a fully valid and independent scale. What is more, not only the Sun mode but all other six planetary modes sound like original, independent modes [with its tonic on the subtones] of the generic tone c5=4096 Hz [...] On the other hand, if one plays the modes on the degrees [subtones] of another planetary generic tone of the common fundamental c = 128 Hz, for example on that of the Moon mode 3328 Hz [28 string segments, see Figure 3], one finds that only the mode belonging to the generic tone [in this case the Moon mode] sounds authentic and that all others sound like species or transposed modes. From this it follows that the degrees of the generic tone c5=4096 Hz [...] are also the rightful degrees for the six other planetary modes as independent scales. Once again readers are referred to the monochord; with this, one can easily convince oneself of the above". If one wishes to tune an instrument according to the suggested method, Table 15 in [1, p.88] explains how to do it step by step.
5.- On the hidden qualities of a tone
What is a tone? This is an interesting question, and perhaps it is on the reader's mind after all that has been discussed so far. I would classify the characteristics of a tone into quantitative and qualitative ones. Quantitative properties are those objectively measurable. The qualitative ones have an effect on us as human beings, despite we don't know how to quantify them yet. Of course, the main quantitative characteristic of a tone is its frequency: how many times per second it cycles. However, when producing a tone with a stringed instrument -such as the simple monochord described in the previous article- not only its fundamental frequency f~1/L is produced. A string of length L can, and indeed does also vibrate at integer multiples of this frequency. This is so because its fixed structure allows the formation of standing waves with two, three and more nodes which "divide" its length into two (L/2), three (L/3), and more fragments, producing overtones or harmonics at 2f = 2/L, 3f=3/L, etc (see Figure 4).
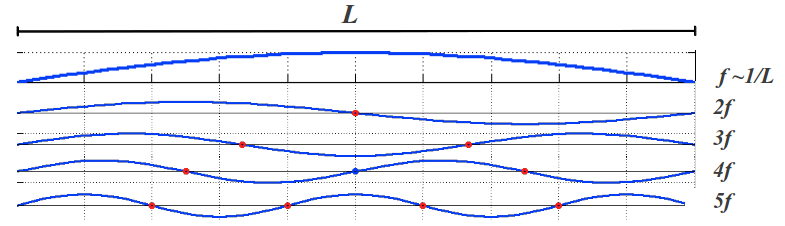 |
|
| Figure 4: Playing a string of length L produces its fundamental frequency f as well as its harmonics 2f, 3f, ... |
Despite the harmonics usually have much lower amplitude that the fundamental, the overall sound produced when a tone is pluck in the string contains a mixture of the string fundamental and all its harmonics. Depending on the exact way the note is played, the harmonics may have different amplitudes. As a result, musicians use to say that the note has a different timbre. The main constituent of timbre is provided by the tone's fundamental frequency and its harmonics, although it is also influenced by time components of the sound such as the temporal envelope, the attack, etc. [2]. In addition, when a given note is played on different instruments, the resulting tone does not have the same timbre, as each instrument produces harmonics of different amplitudes. People have developed subjective rating scales for timbre such us dull/sharp, cold/warm, soft/hard, pure/rich, full/empty, etc. For a more detailed description of timbre see reference [2].
My main question is: can a tone timbre account for the different qualities among distinct tones that the listeners in Maria Renold's experiments have reported? I don't think so for the following reason: the inherent qualitative characteristics of a tone were maintained in different instruments: most people preferred a = 216 Hz over a = 220 Hz despite the instrument in which both tones were played. Therefore the inherent qualitaties of a tone were preserved across instruments, but we know from the above discussion that changing the instrument also changes the timbre of its tones. So timbre does not seem to be what caused people to like or dislike a particular tone above another. In addition, those distinguishing qualities of a tone were not present when the tone was produced electronically.
I have the hypothesis that the inherent qualities of a tone which are experienced independently of the instrument may be closely related to the interaction of the sound source with three dimensional space. The so called empty space is most likely structured. Buckminster Fuller already considered the possibility that the geometric structure of space was given by his Isotropic Vector Matrix (IVM): a network of interconnected tetrahedra and octahedra with a Vector Equilibrium in its center. This is what I have called the inner structure of Metatron's Cube, a structure that scales inwards and outwards, and whose cartesian coordinates can be derived exclusively from integer and rational numbers, in fact from powers of 2 and 3 as in Aristoxenus musical scale. For Fuller, the IVM was a conceptual framework describing the symmetry of space, with which energy events could interact through its jitterbug property, producing a radiating wave of activity [3, p.192]. So my hypothesis is that, depending on the frequency of the sound source, a different geometric energy propagation pattern takes place in empty (structured) space. This geometric pattern may not captured by microphones, but it may interact with the subtle bodies of human beings, and it may be the source of the inherent qualities of sound that we are able to perceive but not yet to quantify.
There is perhaps a simpler hypothesis: the origin of the hidden qualities of sound may be found in the three dimensional energy distribution of sound due to the geometry of the room. Different sound frequencies generate different geometric interference patterns. The sound distribution affects not only our ears, but it may be sensed by our whole human body. This could explain why those geometric properties of sound are loosely captured by a single or a pair of microphones. Finally, the actual mechanism may be a combination of both methods, with (structured) empty space actively involved in the generation and transmission of that geometric pattern linked to a sound source.
6.- References
[1] Renold, Maria: "Intervals, Scales, Tones and the Concert Pitch c = 128 Hz", Temple Lodge, 2004.
[2] Sethares, William A: "Tuning, Timbre, Spectrum, Scale", Springer, 2004.
[3] Edmondson, Amy C.: "A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller", EmergentWorld Press, 2007.