- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Continued Fractions
"Natural phenomena express themselves through number without the need to measure.
Observation and measurement succeeds only in verifying what was already present within number itself.
We can uncover the secrets of number only by holding it up to the light in the proper way".
Jay Kappraff
Table of Contents
1.- Introduction
2.- Basic definitions
3.- Calculating the indices
4.- Calculating the convergents
5.- A graphical procedure: the Farey tree
6.- Continued fractions of irrational numbers
7.- Noble numbers
8.- References
Appendix
1.- Introduction
Beyond integer numbers, we find fractions -also known as rational numbers- which express a relation between two whole quantities (two edges in a polygon, the frequencies of two oscillators, etc.). When written in decimal notation they have either a finite number of decimals, like 235/100=0.235, or an infinite number of repetitive decimals, like 11/7=1.571428571428571428... The other "half" of the movie is played by irrational numbers, those with an infinite, non-repetitive sequence of decimals. Some of them, such as φ=1.6180339887... or π=3.1415926535... play a key role in Sacred Geometry.
The aim of this article is to provide a tool, namely continued fractions, with which any real number, either rational or irrational, can be analysed and its "inner" structure uncovered. Continued fractions allow us to understand why, among the infinite number of sequences that converge to the Golden Ratio φ, Fibonacci sequence is so special; or what does it mean that the Golden Ratio is the most irrational number; or why some special rationals, known as Noble numbers and closely related to φ, play a key role in many natural phenomena such as plant phyllotaxis. In the journey, a hierarchy of rationals known as the Farey Tree, with many implications in physics and chemistry, will emerge in a natural way.
2.- Basic definition
Let's take as an example the fraction 5/12. This number can be expressed in the following alternative way:
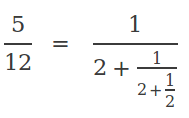
This expression is known as the continued fraction expansion -or simply continued fraction- of number 5/12. In this representation, the numerators are always 1. The interesting part are the whole numbers that appear in the successive denominators. To recover the original number, it suffices to know these numbers; therefore the continued fraction expansion is usually abbreviated as 5/12 = [2, 2, 2]. In general, any real number x between 0 and 1 can be expressed as a continued fraction as follows:
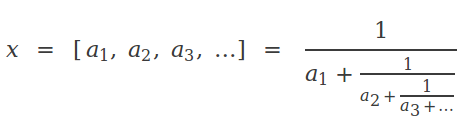
where ak , k=1,2,... are called the indices. The continued fraction expansion is finite if x is rational, and infinite if x is irrational. If the integer part of x is not zero, then the general expression of x becomes
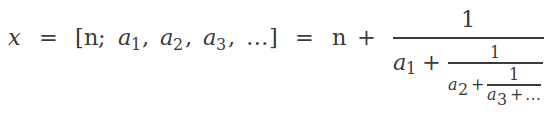
Here we can see that the continued fraction actually expresses the structure of the decimal part of x. Therefore, from now on we shall restrict our analysis to continued fractions of numbers contained between 0 and 1.
3.- Calculating the indices
Let's see how we can calculate the indices of the continued fraction of a given number. First of all we'll focus on the rationals. Consider a rational number expressed as a fraction A/B. The key point here is to notice that, if we invert it B/A, its integer part is the first index a1. Therefore a1 can be obtained by a simple integer division. To obtain the following indices, we only need to iterate the process using the remainder as the new divisor, as shown bellow:

We have stopped the process at the third index, but in general there can be much more indices: the process actually stops when we get a zero remainder. Let's illustrate it with the example given in the previous section, namely the fraction A/B = 5/12:
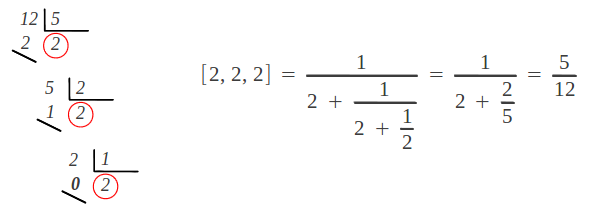
It is important to notice that any continued fraction has two possible representations, because [a1, a2, ..., an,1] is exactly equal to [a1, a2, ..., an+1]. That is to say, when the last index is 1, it can be added to the preceding one leading to an equivalent, more "compact" continued fraction with one less index. In the previous example:
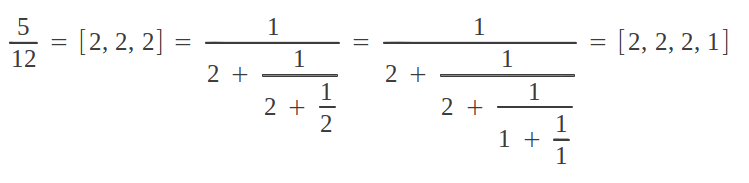
4.- Calculating the convergents
By truncating the continued fraction of a number x = A/B at successive points in its development, we obtain rational approximations Pk/Qk to x called its convergents:
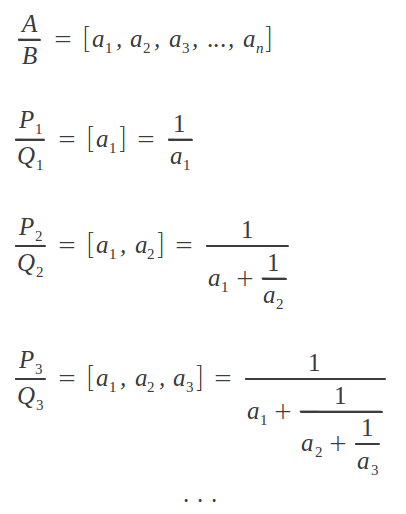
The convergents have the following important property [Kapp]: each convergent Pk/Qk is the best rational approximation to number x for denominators no larger than Qk. Let's calculate the convergents in the previous example:
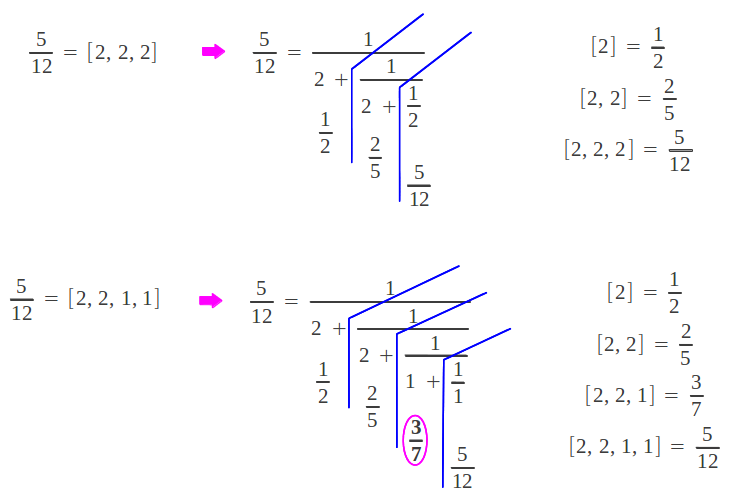
According to the stated property, 2/5 = 0.4 is the best possible rational approximation to 5/12 = 0.4166666 with denominator no larger than 5 (error=4%). Similarly, the "expanded" representation of the continued fraction (the one ending with a 1) provides one extra convergent, namely 3/7 = 0.42857143. This is the best possible approximation to 5/12 with denominator no larger that 7 (error=2.8%). We can observe that using the "compact" representation of a continued fraction "hides" one of the convergents of the expansion. Therefore, it is preferable to work with the equivalent "extended" representation that ends in a 1.
As we add more indices to the convergent, its direct calculation gets more and more difficult. However, there exists an iterative procedure that allows us to calculate a given convergent from the two preceding ones [Kapp]. To initialize the process we need to calculate P1/Q1, for which no previous convergents exist; in this case we assume the initial conditions P-1/Q-1 = 1/0 and P0/Q0=0/1. The overall process can be summarized in the form of a table as follows:

Now we check that this algorithm effectively provides the expected convergents for the "extended" continued fraction representation [2,2,1,1] of 5/12:

5.- A graphical procedure: the Farey tree
Up to now we have learned how to obtain the indices of the continued fraction of a given rational, and to calculate its convergents given those indices. The reader may be wondering: is there an easier way of determining the continued fraction of a rational number? Well, there exists a graphical procedure which allows to somehow "sort" rational numbers and to easily calculate the continued fraction of a given rational. The simplest (shortest) continued fraction after unity [1] = 1/1 is clearly [1,1] = [2] = 1/2. A nearby rational number can be obtained through the mediant between these two rationals, which consists on calculating a new fraction by adding numerators and denominators separately as shown below:
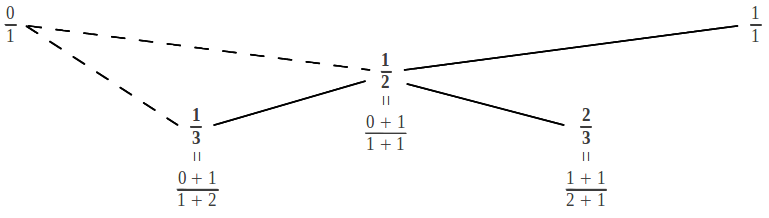
This process generates a new rational contained in between its predecessors, so that we have 0/1 < 1/3 < 1/2 < 2/3 < 1/1. The question is: what are the continued fractions of the newly obtained rationals? They can be easily obtained with the aid of the following tree:
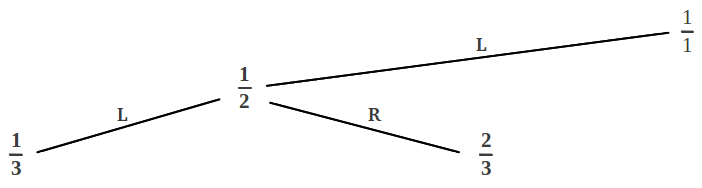
Starting from unity, a descension can be to the left (L) or to the right (R). To obtain the continued fraction of a rational in the tree, we first write down the descending steps in each direction until we reach the number of interest. For example to reach 1/3 we make two left steps [LL]. Then the resulting sequence of L's and R's needs be completed either with an L or with an R: in our example, we have [LLL] or [LLR]. This leads to the two possible representations of the continued fraction that we are searching. The indices in the continued fraction are obtained by counting the consecutive number of equal steps: for example [LLL] has three consecutive L steps so it corresponds to the continued fraction [3], whereas [LLR] has two L steps and one R step, so it corresponds to the continued fraction [2,1]. In both cases, they equal 1/3 as shown below:
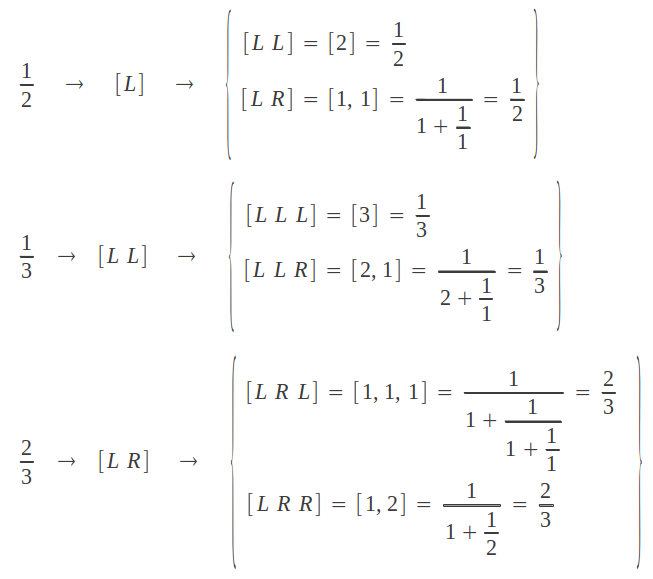
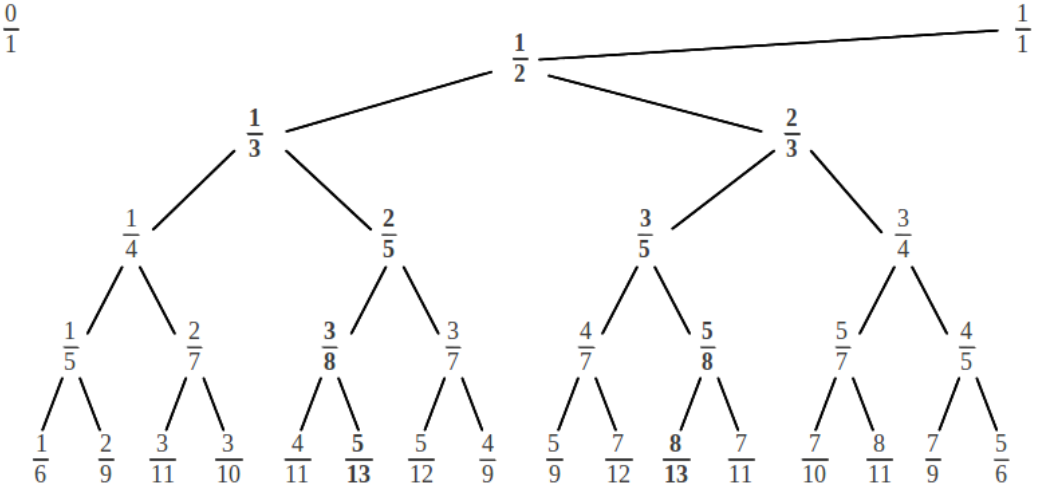
Continuing the process of generating a new rational number in between every pair of the previous existing rationals, we obtain what is known as the Farey tree:
To determine the continued fraction of each rational in the tree, we write down each descending L/R step in the process as follows:
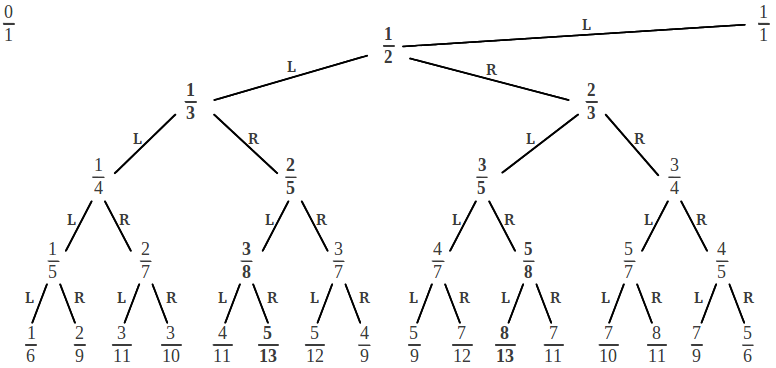
Notice that any rational in this tree can be arrived at by one and only one path down the tree. Then its corresponding continued fraction is easily obtained by counting the sequence of consecutive L-R steps as explained above. The following figure illustrates the Farey tree and the two equivalent representations of the continued fraction of each rational number in the tree:
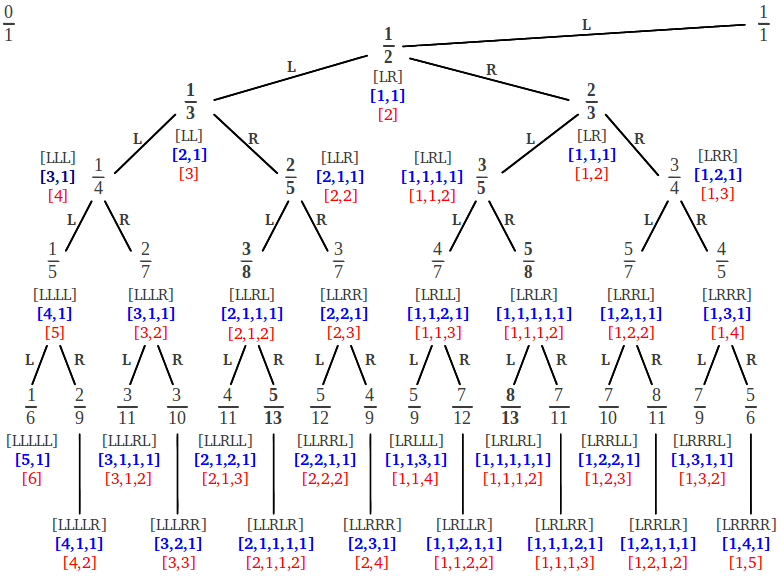
It is worth making several observations concerning the structure of the Farey tree and the corresponding continued fractions:
(1) The sequence of L-R steps that leads to a given rational, with a final L or a final R appended, provides the two equivalent continued fractions of this rational: the "compact" one and the "extended" one. For example to reach 5/12 we follow the sequence of steps [LLRRL]. If we complete this sequence with a final L, we obtain [LLRRLL] = [2, 2, 2]; on the other hand, if we complete it with a final R, we obtain [LLRRLR] = [2, 2, 1, 1] .
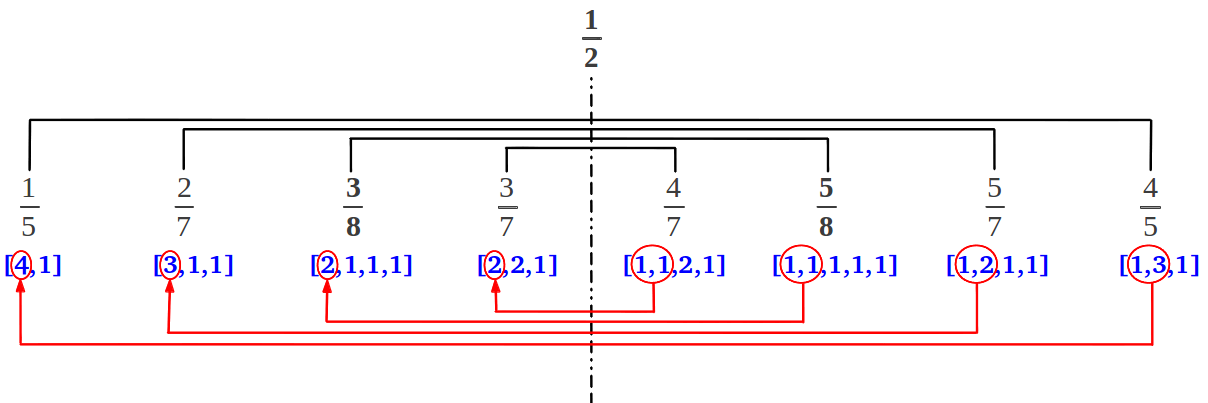
(2) Any new row in the Farey tree has a number of fractions double its preceding row, because a new element is introduced in between each existing pair. In addition, each row has mirror symmetry: if we draw a vertical down 1/2, to each side of this line we find a couple of complementary fractions that add up to 1. For example in the third row, we find 3/7 and 4/7, 3/8 and 5/8, 2/7 and 5/7, and 1/5 and 4/5. Moreover, it suffices to know the continued fraction of the elements located to the right of 1/2: the continued fraction of their complementaries is the same with the leftmost two figures added up, as shown below:
(3) The convergents that lead to a given rational can be directly obtained as the fractions that brace it in an alternating way along the vertical. The first step can be to the left or to the right of the vertical. Each alternative path provides the convergents of one of the two continued fraction representations of the starting rational, as illustrated in the following diagram for the fraction 5/12 (the convergents of [2, 2, 2] in red, and the convergents of [2, 2, 1, 1] in blue):
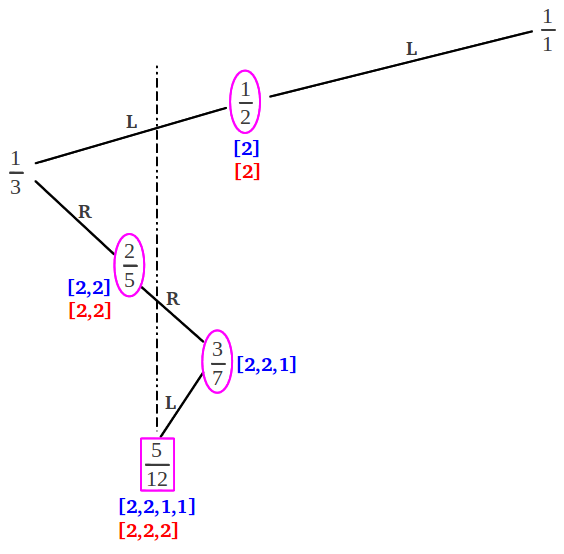
Again it is clear that, in order to recover all the convergents to a given rational, the "extended" continued fraction (ending with a 1) must be used. In summary, the Farey tree contains all the necessary information to obtain both the indices and the convergents of any given rational number, provided we know its exact location in the tree. The following table summarizes the first 32 rational numbers contained in the Farey tree and their corresponding continued fractions:
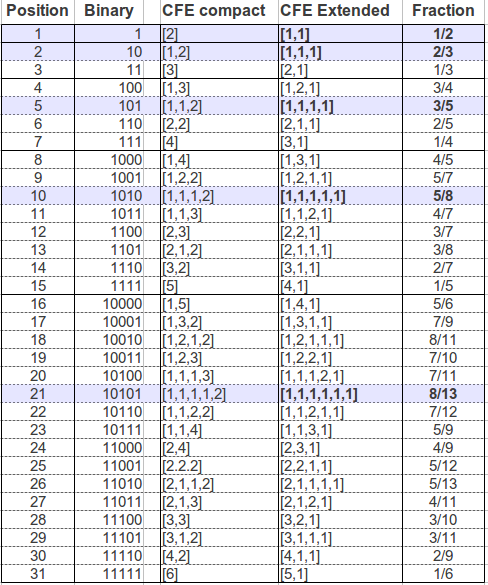
We can see that each row in the Farey tree corresponds to a block of rationals in this table. All the numbers in each block have in common that the indices of their continued fraction add up to the same value: 2 in the first row, 3 in the second, 4 in the third, ... Different continued fractions in a block somewhat describe different ways of splitting the integer value associated to that row. In every block, there is one rational number whose continued fraction is the most dispersed: it is the ratio of two consecutive numbers in the Fibonacci sequence, Fn-1/Fn. If we look back to the tree, we can see that a continued fraction with a sequence of ones corresponds to rational numbers which zigzag down the tree following the steps [LRLR ...] = [1, 1, 1, 1, ...]. It is interesting to note that the complementary numbers to those special rationals in each row are also very dispersed but begin with 2 instead of 1: their sequence is of the type [LLRLRL ...] = [2, 1, 1, 1, ...] . They correspond to the ratio of a Fibonacci number and the number before its predecessor in the sequence, Fn-2/Fn. We shall see in a later section that these rationals are the convergents of two irrational numbers from a family of special irrationals called Noble numbers. Can you guess what irrational numbers do those sequences lead to, in case we let them continue indefinitely?
It is also interesting to notice that each rational number in the table above has been assigned an absolute position, a natural number. The reader can check that this position can be obtained from the Farey tree by numbering the rationals in each row from right to left, starting in the first row and proceeding downwards. The key fact is that those position numbers are not arbitrary: each one is directly related to the continued fraction representation of the corresponding rational. For example, imagine we wanted to know which is the 25th rational in the tree. To proceed we simply need to put down 25 in binary notation, 25 = 11001, and substitute each 1 by a L move and each 0 by an R move. The final result is [LLRRL] which after completion with an L or R gives rise to [2, 2, 2] = [2, 2, 1, 1] = 5/12. Therefore, there is a rational number associated to every natural number according to this process.
6.- Continued fractions of irrational numbers
Up to now we have focused on rational numbers, but what about the irrationals? As we mentioned above, the continued fraction expansion of an irrational number α has an infinite number of indices. This expansion can also be truncated at successive steps, giving rise to the convergents Pk/Qk to the irrational number α. There is a general procedure for calculating the continued fraction representation of any irrational number, provided we know its exact decimal representation (see the Appendix). Some examples of continued fractions of notable irrational numbers are the following [Barr]:

But in this article we are interested in continued fraction expansions of two families of special irrational numbers. These expansions happen to be simple to calculate, and the resulting irrationals have very special properties and can be found in many physical phenomena. A first family is formed by all irrational numbers satisfying the equation x2=px+1, for p=1,2,3, ... This equation can be also expressed as x=p+1/x. After substitution into itself, it provides the following set of expansions, whose resulting irrational numbers can be directly obtained as the positive solution of the second order equation:
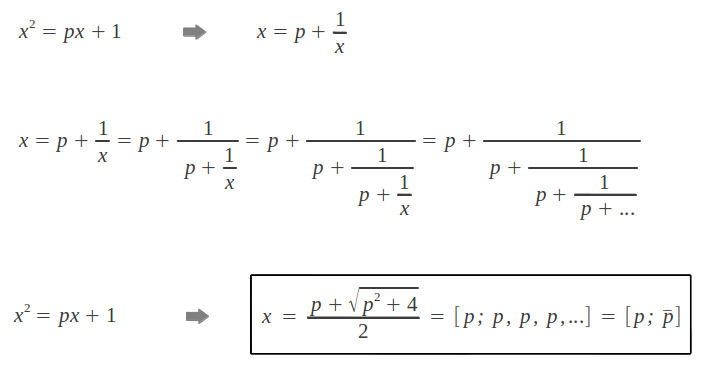
We can observe that all continued fractions in this family have constant indices [p; p, p, p, ...]. They correspond to a set of numbers known as the Metallic Means. As the reader may have noticed, the first number in this family is, of course, the Golden Ratio: φ = [1; 1, 1, 1, 1, ...]. Its decimal part φ - 1 = 1/φ has the expansion [1,1,1,1,...]. Let's calculate the convergents of 1/φ -the convergents of φ will be their inverses- and see if they sound familiar to us:
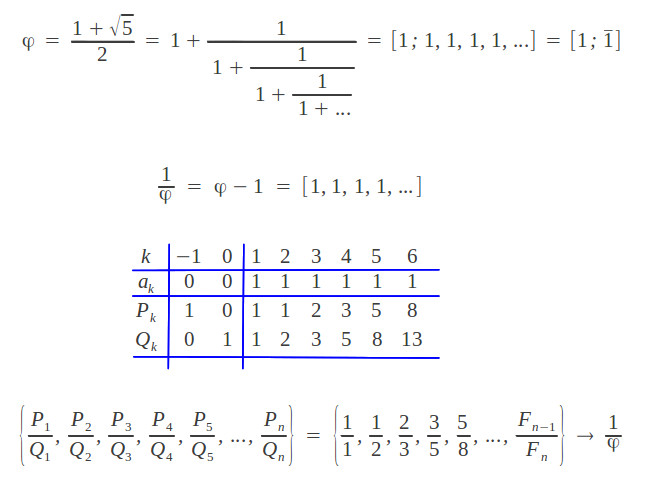
As we can see, the convergents of the inverse of the Golden Ratio are the quotients of successive numbers in the Fibonacci sequence. Can you locate them in the Farey tree? Now my question is the following: among the infinite number of sequences whose consecutive quotients converge to the Golden Ratio why is the Fibonacci sequence so special? Well, according to the general property of the convergents of a continued fraction stated in section 4, the ratio Fn-1/Fn of consecutive values in the Fibonacci sequence is the best possible rational approximation to 1/φ with denominator no larger than Fn (for example, 8/13 is the best rational approximation to 1/φ with denominator no larger than 13).
Now we are also in a position to understand why the Golden Ratio is the most irrational number. The answer is directly related to the degree to which an irrational number α can be successively approximated by the convergents Pk/Qk of its infinite continued fraction expansion. A measure of the approximation of Pk/Qk to α is given by [Kapp]:
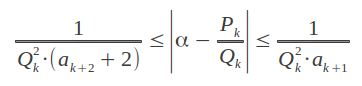
In other words, the convergents of α corresponding to large values of the indices ak approximate α more closely because |α - Pk/Qk| is small. For example, approximating π by the fifth convergent in its continued fraction expansion given above provides a very accurate value -good to nine decimal places, see the Appendix- because the index a5 is very large: P5/Q5 = [3,7,15,1,292] = 3.141592653012...
Now consider α = 1/φ in the pevious inequality. Since all the indices of its continued fraction expansion are equal to 1, it is the irrational number with the poorest approximation to its convergents. And as the convergents are the best rational approximation to their limiting irrational, 1/φ is the irrational number which is further apart of the rationals than any other irrational -whose indices in the continued fraction expansion will necessarily be greater than one.
7.- Noble numbers
Any irrational number contained between 0 and 1 whose continued fraction expansion is of the form τG = [a1, a2, ..., an, 1, 1, 1, ...], where ak≥1, is called a Noble number. The noblest number is the inverse of the Golden Ratio 1/φ = [1, 1, 1, 1, ...]. The next noble number in importance is 1/φ2 = [2, 1, 1, 1, ...]. It is very instructive to see where the convergents of these numbers are located in the Farey tree. As we mentioned above, a continued fraction with a finite sequence of ones corresponds to rational numbers which zigzag down the Farey tree following the steps [LRLR ...] = [1, 1, 1, 1, ...]. The inverse Golden Ratio starts zigzagging from the very beginning. Any other Noble number starts zigzagging later, after some finite number of steps in the tree which are not an exact L-R sequence. From a given rational number, for example 5/12, there are two ways in which one can start zigzagging downwards: either from the fraction immediately above and to the right of 5/12, in this case 3/7; or from the fraction immediately above and to the left of 5/12, that is 2/5:
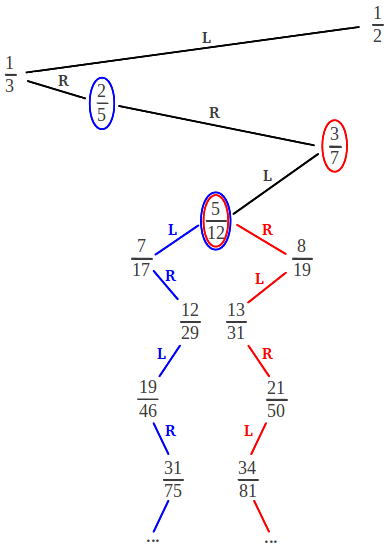
The resulting infinite continued fraction converges to two irrational numbers, one located to the right and the other to the left of the starting rational, in this case 5/12. Jay Kappraff has demonstrated that the resulting irrational number τG has the general formula [Kapp]:
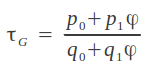
where p1/q1 is the starting fraction and p0/q0 is the one immediately above it in the tree, either to the left or to the right. In our example, the two Noble numbers "generated" by 5/12 are the following:
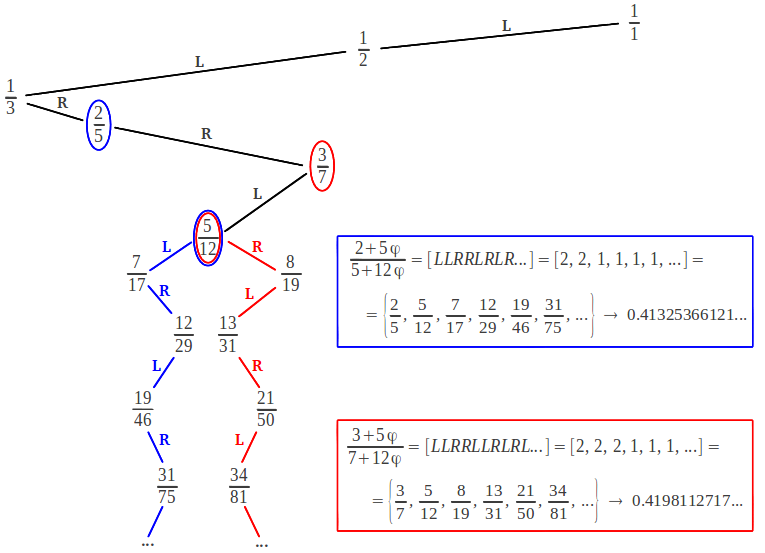
It is interesting to notice that when the zigzagging process starts, every new convergent down the tree is obtained by direct mediant addition of the two preceding ones. This a very important property that all Noble numbers share with the Golden Ratio. It is usually stated by saying that Noble numbers have no intermediate convergents -of course below its "generating" fraction, in our example 5/12. In the path down the tree, this means that there is no step that passes through an intermediate fraction (further apart from the vertical) which is not a convergent, something which only happens when we make consecutive LL... or RR... steps: for example, to arrive at 5/12 we need to pass through 1/3, which is not a convergent of the continued fraction of 5/12, but it is located "in between" the convergents 1/2 and 2/5 in the descension through the Farey tree.
Noble numbers also share with the Golden Ratio the property of being the "most irrational" numbers, because of the tail of 1's in their continued fraction expansion. These two properties account, on the one hand, for their occurrence in the study of plant phyllotaxis. Quoting Jay Kappraff [Kapp, p. 325]: "When noble numbers are multiplied by 360 degrees, they yield special angles related to the growth of plants known as divergence angles. These angles describe the placement of florets on the surface of a plant such as the florets that result in the spiral whorls of a sunflower. For example the irrational [2,1,1,1,...] = 1/φ2 is the most prevalent number, and it leads to the angle 360/φ2 = 137.5 degrees. The next most important angle is [3,1,1,1,...] which, when multiplied by 360 yields 99.5 degree. The next angle in importance is [2,2,1,1,1,...] and gives rise to 151.1 degree".
The fact that Noble numbers are the most poorly approximated by any rational number makes them also important in many chaotic orbit problems in physics. John D. Barrow explains it in an elegant way [Barr]: "These numbers characterise the frequencies of undulating motions which are the least susceptible to being perturbed into chaotic instability. Typically, a system which can oscillate in two ways, like a star that is orbiting around a galaxy and also wobbling up and down through the plane of the galaxy, will have two frequencies determining those different oscillations. If the ratio of those frequencies is a rational fraction, then the motion will ultimately be periodic, but if it is an irrational number then the motion will be non-periodic, exploring all the possibilities compatible with the conservation of its energy and angular momentum. If we perturb a system that has a rational frequency ratio, then it can easily be shifted into a chaotic situation with irrational frequencies. The Golden Ratio is the most stable because it is farthest always from one of these irrational ratios. In fact, t he stability of our solar system over long periods of time is contingent upon certain frequency ratios lying very close to Noble numbers".
8.- References
[Kapp] Kappraff, Jay: "Beyond Measure: a guided tour through Nature, Myth and Number", World Scientific Publishing, 2002.
[Barr] Barrow, John D: "Chaos in numberland: The secret life of continued fractions", Plus Magazine, 2000.
Appendix: Calculating the continued fraction of a real number
What about irrational numbers? Except in some particular cases that we have explored in the preceding sections, to calculate the continued fraction of an irrational number we need to know its decimal representation. If this is the case, then we can follow a similar process as in Section 4 above, but in order to obtain the "quotients" of a real division we exact need to take the integer part of the result. We shall denote the integer part of a number α as [α]. The general process goes as follows: if the number α is greater than 1, then we take apart its integer part a0 = [α]. To obtain the first index in the denominator, a1, we only need to invert the number and take its integer part. Then the process of inverting and taking the integer part can be iterated as many times as needed:
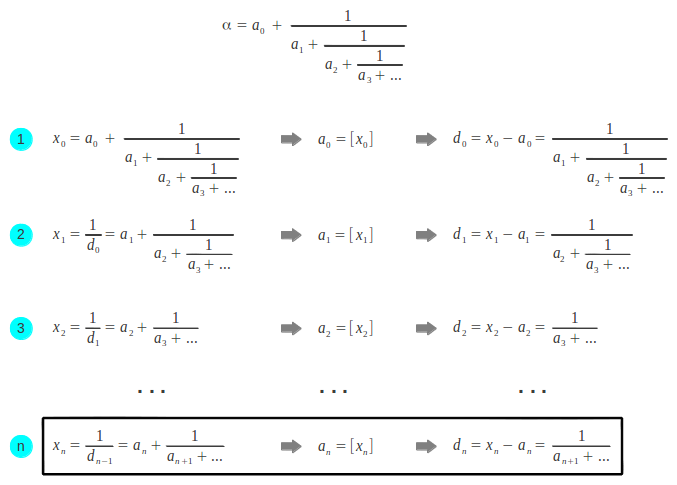
When should we stop the process? The continued fraction of an irrational number has an infinite number of indices. The continued fraction resulting from stopping this process at a given iteration provides an approximation to the original number. The more indices we calculate, the better the approximation. However, if the original number is known to a finite number of decimals, we are actually limited by this constraint. Imagine that we want to obtain the continued fraction of π knowing its decimal representation up to ten decimal places. The operations would go as follows:

Once we have the indices of the continued fraction, the convergents may be recovered by the same algorithm that applies to rational numbers as explained in section 5. In our example, this allows us to calculate successive approximations to number π. Each of them, being the convergent of a continued fraction, is the best approximation among the ones with no larger denominators:

It is interesting to point out that the approximation π≈355/113 was already known to the early Chinese [Barr]. And the approximation π≈22/7 is found in the Great Pyramid of Gizeh, and it allows a very good approximation to the squaring of the circle, as we have seen in this article.
Last updated:
20/01/2014
