1.- Introducción

En este artículo voy a mostrar que la razón Aurea $$ φ proporciona un enlace cuantitativo entre varias cantidades conocidas de la física atómica. En su mayor parte está basado en las extensas investigaciones de Dr. Rajalakshmi Heyrovska. El lector interesado puede encontrar un resumen de su investigación en este capítulo de libro titulado "La razón Aurea de las creaciones de la Naturaleza aparece en la arquitectura de los átomos y los iones".

Mientras buscaba los valores exactos de los radios iónicos y el significado del potencial de ionización del hidrógeno, la Dra. Heyrovska ha encontrado que el radio de Bohr puede dividirse en dos secciones Aureas que pertenecen al protón y al electrón. Más en general, ha descubierto qu$$e φ es también la relación entre el radio aniónico y catiónico de cualquier átomo, siendo su suma la longitud del enlace covalente. Después de esto ella demostró, entre otras cosas, que las longitude de muchos enlaces en moléculas orgánica e inorgánicas se comportan de forma aditiva, y que son la suma de los radios iónicos y/o covalentes, ya sea parcial o totalmente iónicos o covalentes. Además, ha descubierto una nueva interpretación en términos del Angulo Aureo que proporciona un valor muy preciso de la constante de Estructura Fina α^-1.

2.- La Razón Aurea, el radio de Bohr y la energía de base del Hidrógeno

El radio de Bohr del estado base del hidrógeno atómico, $a_B=\mathrm{0.00529nm}$, está definido como

$$a_B=\frac{1}{2}\frac{e^2}{4\pi {\epsilon }_0{E}_H}$$

donde $e$ es la carga del electrón, ${\epsilon }_0$ es la permitividad del vacío, $E_H$ es la energía en estado base y $I_H$ es el potencial de ionización del hidrógeno. Recientemente se ha mostrado mediante métodos de densidad funcional que el radio de enlace del hidrógeno con el carbono es $a_B\mathrm{/\phi }=\mathrm{0.00327nm}$. Esto ha motivado el descubrimiento por parte de la Dra. Heyrovska [1] de que $a_B\mathrm{}$, la distancia entre el electrón  $e^{\mathrm{-}}$y el protón $p^{\mathrm{+}}$, puede dividirse en el punto de neutralidad de carga en dos secciones Aureas de la forma siguiente:

$$a_B=\frac{a_B}{\phi }+\frac{a_B}{{\phi }^2}=a_{\mathrm{Be}}+a_{\mathrm{Bp}}$$

donde $a_B\mathrm{/}{a}_{\mathrm{Be}}=a_{\mathrm{Be}}\mathrm{/}{a}_{\mathrm{Bp}}=\phi$. La Figura 1 ilustra esta división (junto con más detalles que se explicarán más adelante) mostrando un círculo de radio $a_{\mathrm{Be}}$ alrededor del electrón $e^{\mathrm{-}}$, un círculo de radio $a_{\mathrm{Bp}}$ alrededor del protón $p^{\mathrm{+}}$, y un círculo de radio $a_B$ que contiene a ambos:

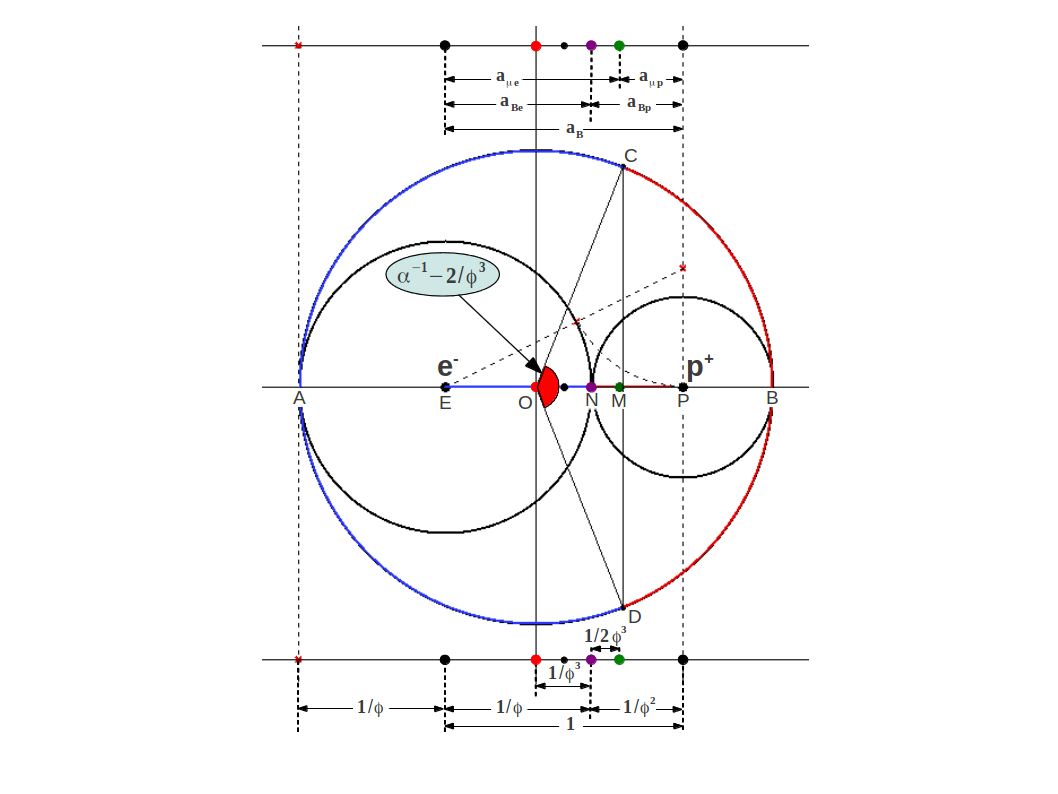Figura 1: El radio de Bohr $\mathrm{EP}=a_B$ del átomo de hidrógeno se divide en las secciones Aureas $\mathrm{EN}=a_{\mathrm{Be}}$ y $\mathrm{NP}=a_{\mathrm{Bp}}$ en el punto de neutralidad eléctrica N, como deja claro el triángulo rectángulo auxiliar. El centro magnético está ubicado en el punto M, a una distancia $a_B/2{\phi }^3$ del punto de neutralidad eléctrica hacia el protón. La circunferencia del círculo exterior también se divide en dos arcos Aureos CAD y CBD mediante el Angulo Aureo. Nótese que la longitud de cada arco es igual al perímetro de las circunferencias internas. El arco más corto está íntimamente relacionado con la constante de Estructura Fina, cuyo valor es muy cercano al Angulo Aureo mostrado en rojo. Además, la cuerda CD intersecta la horizontal muy cerca del centro magnético M.

El hecho de que el radio de Bohr $a_{\mathrm{B }}$se divida en secciones Aureas le confiere la propiedad siguiente (no evidente a simple vista)

$$\frac{1}{a_B}=\frac{1}{a_{\mathrm{Bp}}}-\frac{1}{a_{\mathrm{Be}}}$$

Ello muestra que la propia energía del átomo de hidrógeno en el estado base puede expresarse como la diferencia de dos términos:

$$E_H=\frac{1}{2}\frac{e^2}{4\pi {\epsilon }_0{a}_{\mathrm{Bp}}}-\frac{1}{2}\frac{e^2}{4\pi {\epsilon }_0{a}_{\mathrm{Be}}}=\frac{1}{2}\frac{e^2}{4\pi {\epsilon }_0}[\frac{1}{a_{\mathrm{Bp}}}-\frac{1}{a_{\mathrm{Be}}}]$$

3.- La Razón Aurea y los g-factores

Los g-factores del electrón y el protón ($g_e=2.0023193$ y $g_p=5.58569468$ respectivamente) son medidas de las anomalias de su momento magnético. Ellos también están relacionados con la Razón Aurea de la forma siguiente:

$$g_p{a}_{\mathrm{\mu p}}=g_e{a}_{\mathrm{\mu e}}$$

donde

$$a_{\mathrm{\mu e}}=a_e+\frac{a_e-a_p}{2}=\frac{a_B}{\phi }+\frac{a_B}{2{\phi }^3}$$

$$a_{\mathrm{\mu p}}=a_p-\frac{a_e-a_p}{2}=\frac{a_B}{{\phi }^2}-\frac{a_B}{2{\phi }^3}$$

Esto muestra que el centro magnético del átomo de hidrógeno (punto M en la Figura 1) está desplazado respecto al punto de neutralidad de carga hacia el protón una cantidad $a_B/2{\phi }^3$ (ver la Figura 1).

Las ecuaciones precedentes implican que

$$\frac{g_e}{g_p}=\frac{a_{\mu p}}{a_{\mu e}}=\frac{{\phi }^3-2}{{\phi }^3+2}$$

o de forma equivalente que

$$\frac{g_p-g_e}{g_p+g_e}=\frac{2}{{\phi }^3}$$

4.- La Razón Aurea y la longitud del enlace de moléculas diatómicas

En general, la longitud d(AA)=2d(A) de cualquier enlace covalente AA también puede considerarse como la suma de dos componentes Aureas d(A+) and d(A-) dadas por

$$d\left(A\right)=d\left(\mathrm{A+}\right)+d\left(\mathrm{A-}\right)=\sqrt{2}{a}_A$$

donde

$$d\left(\mathrm{A-}\right)=d\left(\mathrm{AA}\right)/\phi$$

y

$$d\left(\mathrm{A+}\right)=d\left(\mathrm{AA}\right)/{\phi }^2$$

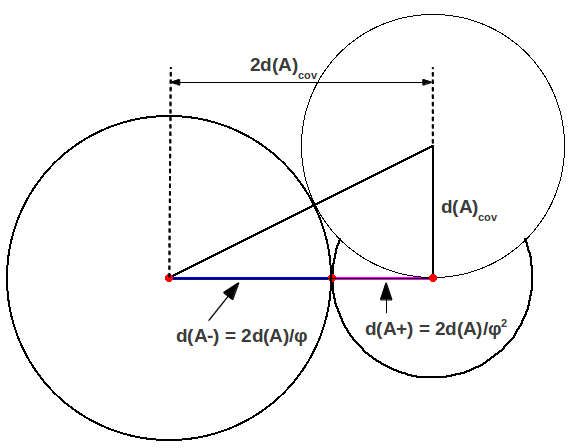
Estas corresponden a los radios, o en realidad las longitudes de los enlaces aniónico y catiónico. Esto se ilustra en la Figura 2, donde se puede apreciar que el radio de Bohr  $a_A\mathrm{}$ es el lado de un cuadrado cuya diagonal es $d\left(\mathrm{AA}\right)=\sqrt{2}{a}_A$. La Figura 3 muestra el caso particular del hidrógeno, la molécula diatómica más simple.

Figura 2: División Aurea de un enlace covalente general.

 

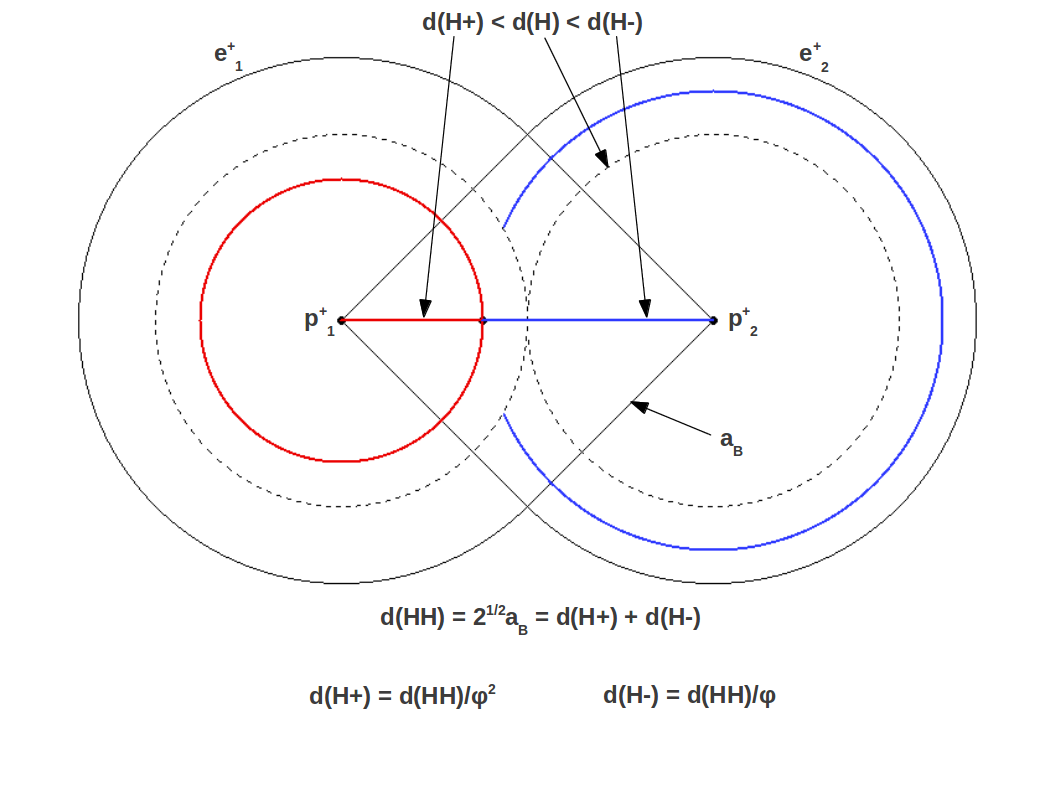Figura 3: División Aurea del enlace covalente en la molécula de hidrógeno

Esta teoría puede extenderse incluso a longitudes de enlaces entre átomos distindos. La Figura 4 muestra un ajuste muy bueno entre los enlaces experimentales de diversos compuestos y los valores calculados como las sumas de dos radios ambos covalentes, uno covalente y otro iónico, o los dos iónicos (ver tabla 3 en [1]):

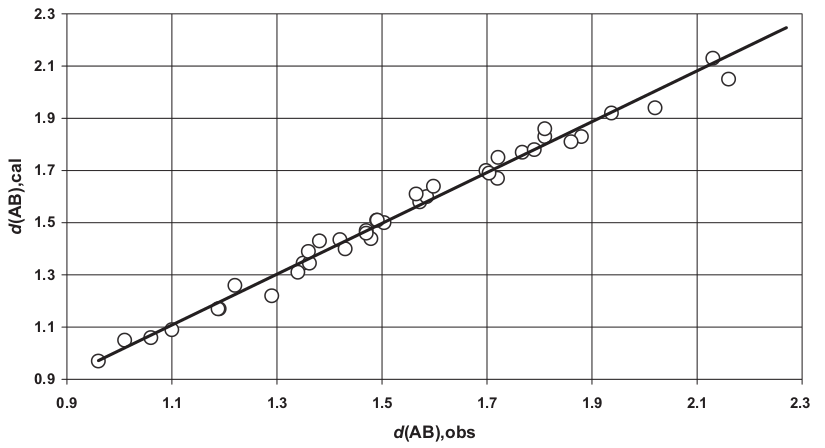Figura 4: Ajuste muy bueno entre la suma de distancias de enlace calculada d(AB), cal y los valores observados d(AB),obs. Todos los valores en Amstrongs [1].

5.- La Razon Aurea y la constante de Estructura Fina

Desde que Sommerfeld introdujo la constante de Estructura Fina en la física, esta ha intrigado a muchos científicos como Eddington, Dirac y otros. Citando a Feynman [2]: “ ... ¿está relacionada con pi o tal vez con la base de los logaritmos naturales? Nadie lo sabe. Es uno de los grandes condenados misterios de la física: un número mágico que nos llega sin ninguna comprensión humana. Se podría decir que la "mano de Dios" escribió ese número, ...".  α se define como $$\alpha =\frac{e^2}{2{\epsilon }_{0}c}$$

donde $e$, ${\epsilon }_0$, h y c son, respectivamente, la carga del electrón, la permitividad eléctrica del vacío, la constante de Planck y la velocidad de la luz en el vacío, y si su valor es constante o no aún se está debatiendo.

La Dra. Heyrovska ha propuesto otra interpretación de α basada en la observación de que su valor inverso es muy cercano al Angulo Aureo. En la Figura 1 se puede observar que el círculo externo se ha dividido en dos arcos Aureos, de longitud $\mathrm{2\pi }/{\phi }^2$ (porción verde) y $\mathrm{2\pi }/{\phi }^2$ (porción azul). La parte pequeña corresponde al Angulo Aureo $360/{\phi }^2$ mostrado en rojo en el centro.

El inverso de la constante de estructura fina es igual a este ángulo más una pequeña corrección que se puede calcular de dos formas distintas. En la forma directa, el factor de corrección es
$$\alpha -\frac{{\phi }^2}{360}=\frac{1-\gamma }{\gamma }$$

donde $(1-\gamma )/\gamma$ está relacionado con el avance del perihelio en la teoría de Sommerfeld [3] y γ es el factor relativista

$$\gamma ={(1-{\alpha }^2)}^{\mathrm{1/2}}=\mathrm{0.99997(3)}$$

Pero en la forma inversa, la constante de Estructura Fina también puede formularse por primera vez exclusivamente en términos de la Razon Aurea de la forma siguiente:

$$\frac{360}{{\phi }^2}-{\alpha }^{-1}=\frac{a_{\mu e}-a_{\mu p}}{a_B}=\frac{g_p-g_e}{g_p+g_e}=\frac{2}{{\phi }^3}$$

con lo cual

$${\alpha }^{-1}=\frac{360}{{\phi }^2}-\frac{2}{{\phi }^3}=\mathrm{137,03562809}$$

que coincide con el valor oficial según CODATA ${\alpha }^{-1}=\mathrm{137.035999074(44)}$con un error tan pequeño como $$ ± 0.00027% (vease la Figura 1).

Referencias

[1] Heyrovska R., "The Golden ratio, ionic and atomic radii and bond lengths", Molecular Physics, 103, pp.877-882.
[2] Tomonaga S-I., Schwinger J. and Feynman R. P.,http://nobelprize.org/physics/laureates/1965/
[3] Ruark A.E., Urey H.C., "Atoms, molecules and quanta", Volume 1, Dover Publications, New York, 1964, p.134.