- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Phi en el cuerpo humano
1.- Introducción
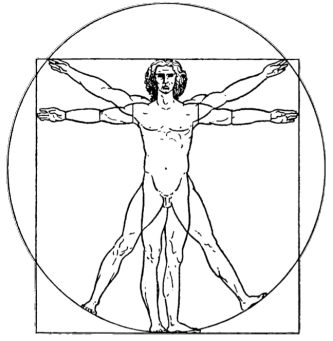
Marcus Vitruvius Pollio, arquitecto romano (25 B.C.), destacaba la similitud entre el cuerpo humano y un edificio perfecto: "La Naturaleza ha diseñado el cuerpo humano de forma que sus miembros estén proporcionados a su estructura como un todo." Él inscribió el cuerpo humano en un círculo y un cuadrado, las dos figuras consideradas imágenes de la perfección. Está ámpliamente aceptado que las proporciones del cuerpo humano siguen la Razón Aurea. En este artículo revisamos diversos estudios al respecto. Mostraremos los hallazgos de Adolf Seizing en el siglo XIX de la Razón Aurea en el cuerpo humano, en realidad aproximada mediante medidas en sucesión de Fibonacci. A continuación examinaremos las proporciones aureas en el cuerpo humano propuestas por los arquitectos Erns Neufert y Le Corbusier en el siglo XX. Por último, mostraremos un estudio simultáneo con una muestra poblacional alemana y otra india que confirma la presencia de la Razón Aurea en algunas proporciones del cuerpo humano.
2.- Proporciones Aureas en el cuerpo humano halladas por Adolf Zeising
Adolf Zeising, allá por el siglo XIX, estaba principalmente interesado por las matemáticas y la filosofía. Pero al retirarse empezó sus investigaciones sobre las proporciones en la naturaleza y el arte. En el campo de la botánica, descubrió la Razón Aurea en la disposición de las ramas a lo largo del tallo de las plantas, y de las venas en las hojas. A partir de aquí extendió su investigación al esqueleto de los animales y las ramificaciones de sus venas y nervios, a las proporciones de compuestos químicos y la geometría de cristales, etc. , y finalmente a las proporciones humanas y artísticas. El título de su primera publicación en 1854 resume su programa: Nueva teoría de las proporciones del cuerpo humano, desarrolladas a partir de una ley morfológica básica hasta ahora desconocida, y que está presente en toda la naturaleza y el arte, acompañado por un resumen completo de los sistemas prevalentes [1]. Esa ley universal era, en efecto, la Razón Aurea. En ella presenta sus propios análisis de las proporciones en el cuerpo humano (Figura 1).
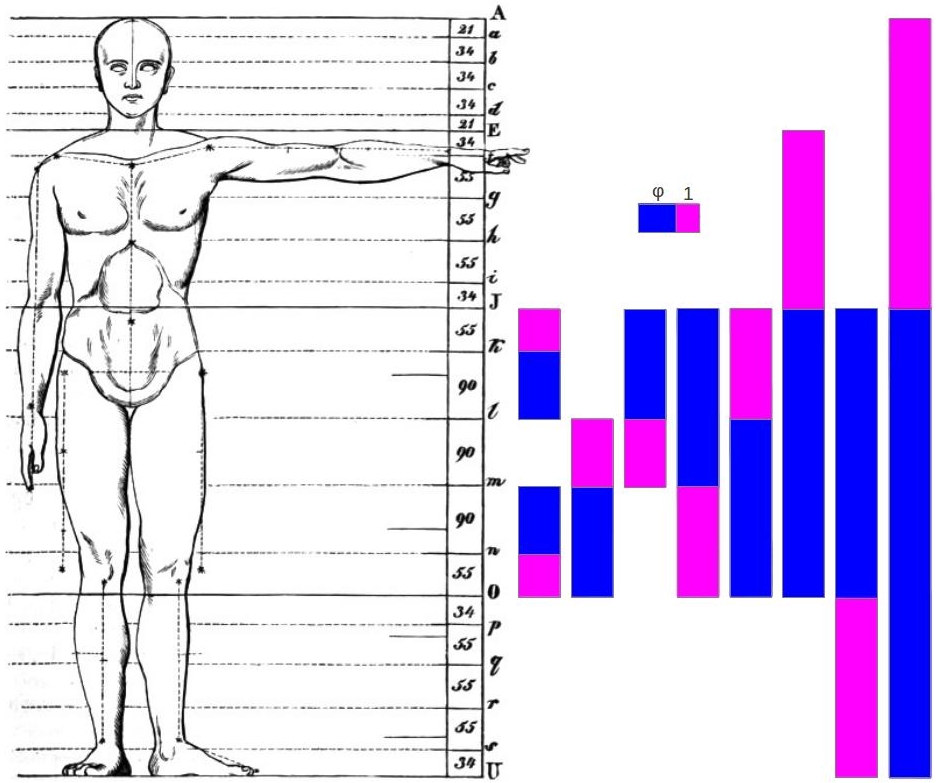 |
| Figura 1: Proporciones Aureas en el cuerpo humano halladas por Zeising [1]. |
Zeising divide la altura total del cuerpo del hombre en cuatro zonas prinxipales: de lo alto de la cabeza al hombro, del hombro al ombligo, del ombliho a la rodilla, y de la rodilla a la planta del pie. A su vez cada zona se subdivide en cinco segmentos, que están dispuestos simétricamente dentro de cada zona: ya sea siguiendo el patrón ABBBA o ABABA, pero siempre sumando 2A+3B. A propósito, la proporción 3/2 en cada zona es un Quinto Perfecto en la escala musical del temperamento justo. ¿Está la música involucrada en el diseño de nuestro propio cuerpo?
En la parte derecha de la Figura 1 se pueden apreciar las proporciones Aureas presentes en cada segmento, y entre segmentos, a diferentes escalas. Las proporciones del cuerpo humano según Zeising son un bonito ejemplo de cómo la Naturaleza aproxima fielmente la Razón Aurea mediante una serie de medidas en sucesión de Fibonacci. Zeising sustituye por error 90 por 89 en sus medidas, pero nosotros hemos usado el valor exacto en los cálculos siguientes. Los números de Fibonacci presentes en su esquema, explícitamente (verde) o implícitamente como totales (magenta), son los siguientes:

Agrupando consecutivamente cada par de medidas adyacentes se obtiene una división iterada del segmento mayor (987) en números de Fibonacci consecutivos que aproximan de cerca la Razón Aurea (Figura 2a). Esto nos recuerda la potencia de la Razón Aurea para dividir un segmento de forma consecutiva por medio de simples sumas y restas después de la primera partición (Figura 2b). Esta serie de divisiones en Razón Aurea también nos recuerda la naturaleza fractal detrás del diseño de nuestro cuerpo, ya que la misma proporción Aurea se repite a todas las escalas.
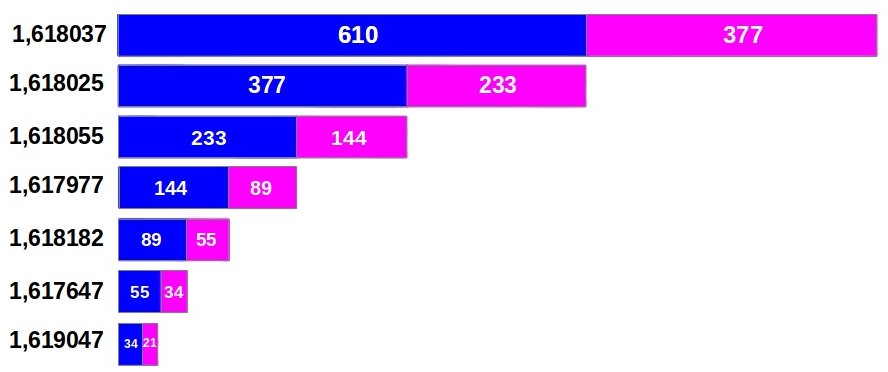 |
| (a) |
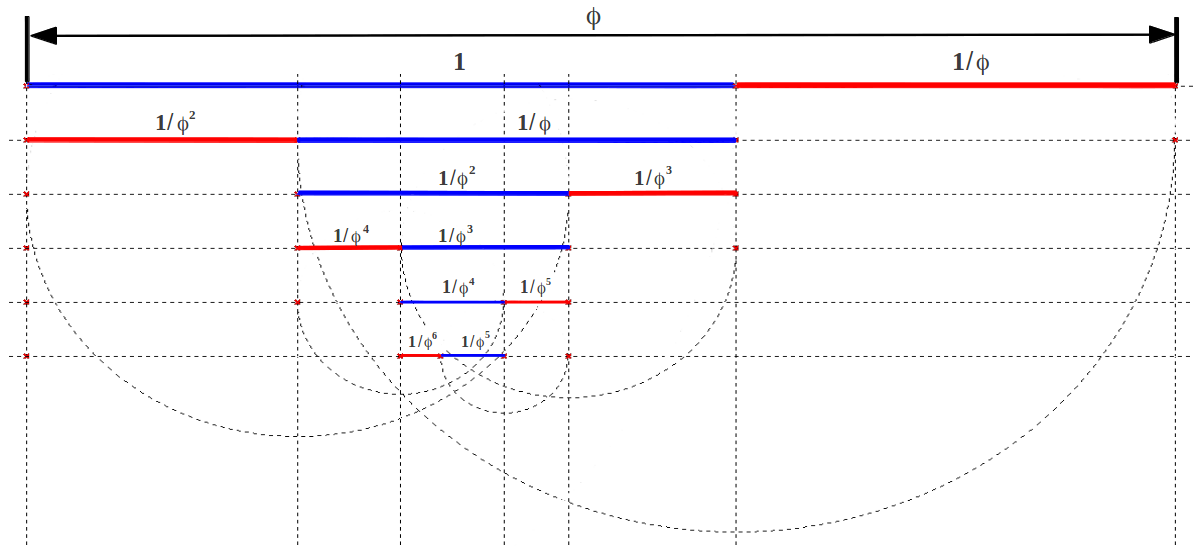 |
| (b) |
| Figura 2: División iterada de un segmento (a) según los números de la sucesión de Fibonacci y (b) según la Razón Aurea. |
3.- Las proporciones Aureas propuestas por los arquitectos Neufert y Le Corbusier
En el siglo XX el arquitecto Erns Neufert (1900-1986) propagó la Razón Aurea como el principio arquitectónico de la proporción en el cuerpo humano. Neufert no sigue estrictamente las proporciones de Fibonacci propuestas por Zeising, sino que en su lugar introduce la Razón Aurea exacta [2] (Figura 3). Para él, la sección Aurea también proporciona el enlace principal entre todas las armonías en arquitectura.
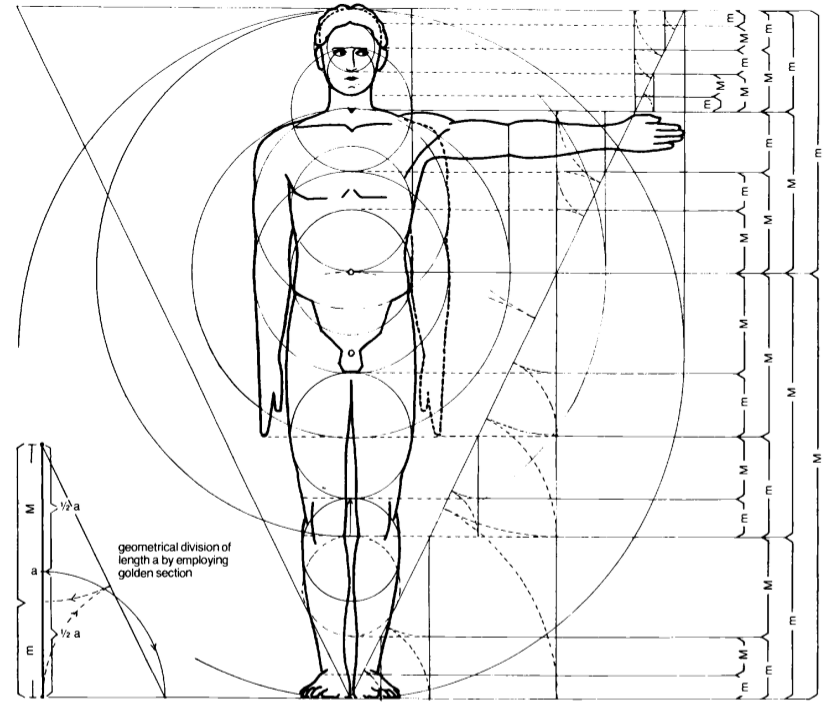 |
| Figura 3: Proportiones Aureas en el cuerpo humano según Ernst Neufert [2]. |
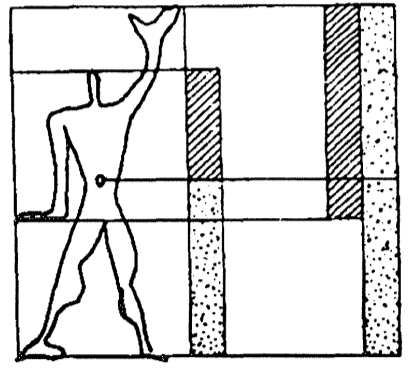
Existe otro gran sistema de proporciones corporales del siglo XX conocido como el Modulor, propuesto por Le Corbusier (1887-1965). En su manifiesto Vers une architecture, presenta la Razón Aurea como un ritmo natural, incorporado de nacimiento en todo organismo humano. Para más detalles sobre el origen histórico y el desarrollo del Modulor I y II se puede examinar el excelente resumen a cargo del arquitecto Manel Franco [3]. La Figura 3 muestra las proporciones esenciales del cuerpo humano propuestas por Le Corbusier:
 |
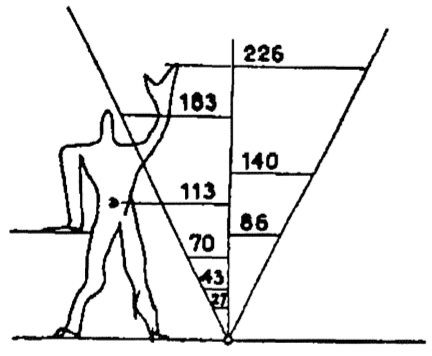 |
| Figura 3: Esquema simple y principales proporciones Aureas en el cuerpo humano según Le Corbusier [3]. | |
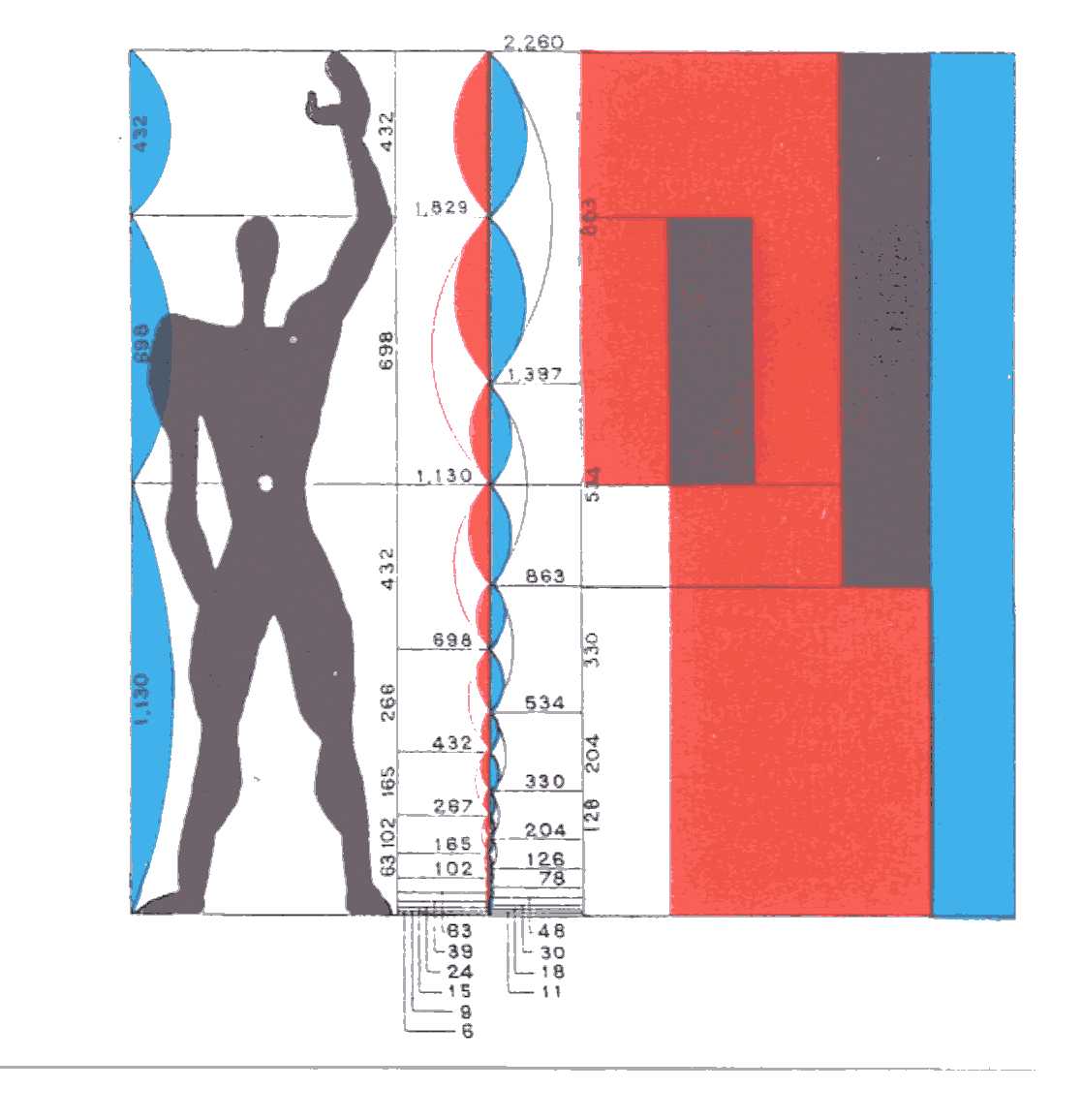
En su versión final, el sistema Modulor II propone dos progresiones de medidas Aureas para el cuerpo humano (Figura 4a). Volviendo al estilo de Zeising, estas progresiones son en realidad medidas en sucesión de Fibonacci (Figura 4b). Es decir, cada medida se obtiene a partir de la suma de las dos precedentes. Por lo tanto, el cociente de cualquier par de medidas consecutivas en estas progresiones aproxima la Razón Aurea.
 |
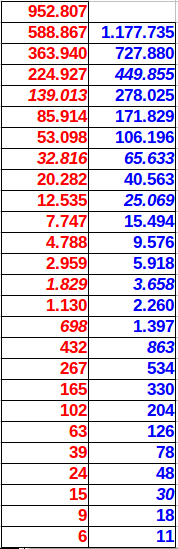 |
| (a) Proporciones Aureas en el cuerpo humano propuestas el el Modulor II de Le Corbusier. | (b) Detalle de las progresiones roja y azul (en mm) en el Modulor II. Los valores en cursiva se desvían ligeramente (1mm) de una sucesión de Fibonacci exacta. |
| Figura 4 | |
4.- Un estudio de campo
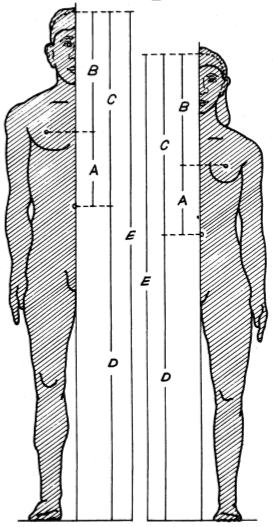
T. Antony Davis, del Indian Statistical Institute (India) y Rudolf Altevogt, del the Zoologisches Institut der Universitat (Alemania) realizaron un estudio donde se medían 207 estudiantes alemanes y 252 jóvenes de Calcuta [4]. Las medidas tomadas A,B,C,D y E se muestran en la Figura 5a. En sus resultados pudieron confirmar que la altura total del cuerpo y la altura desde los pies hasta el ombligo siguen la Razón Aurea (cocientes D/C y E/D). La Figura 5b resume los principales resultados obtenidos. Se obtuvo casi el valor perfecto 1.618 en la muestra alemana (y este valor era válido tanto para chicos como para chicas) y el valor ligeramente diferente 1.615 en la muestra india.
 |
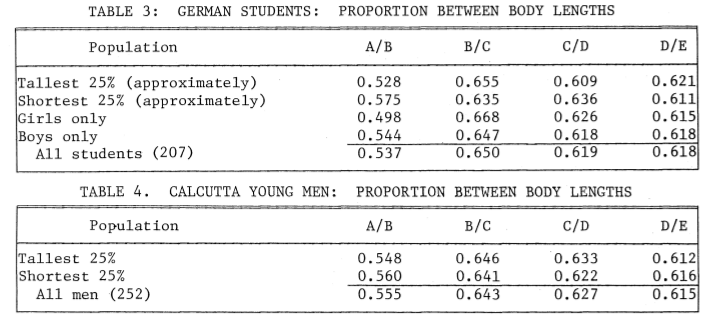 |
| (a) Las medidas tomadas en el estudio [4] | (b) Cocientes promedio resultantes, clasificados por grupos [4]. |
| Figura 5 | |
5.- Referencias
[1] Zeising, Adolf: Nueva teoría de las proporciones del cuerpo humano, desarrolladas a partir de una ley morfológica básica hasta ahora desconocida, y que está presente en toda la naturaleza y el arte, acompañado por un resumen completo de los sistemas prevalentes. (en alemán).
[2] Neufert, Ernst: Architects Data.
[3] Franco, Manel: El Modulor de Le Corbusier (1943-54)
[4] T. Antony Davis and Rudolf Altevogt, "Golden Mean of the Human Body".
