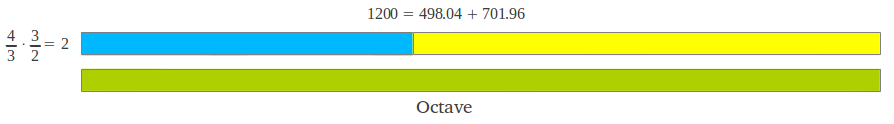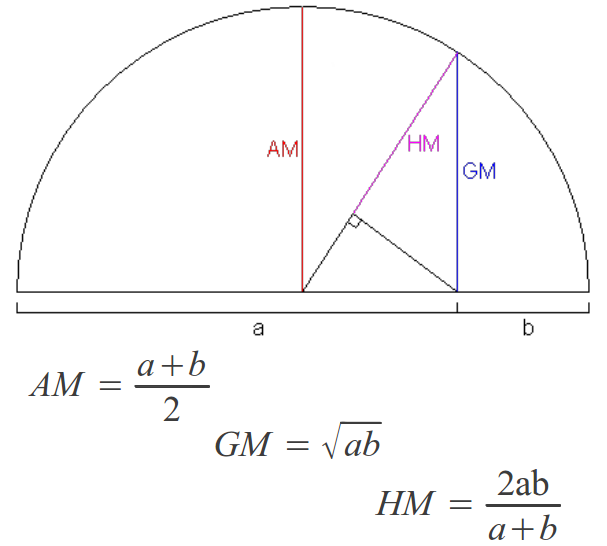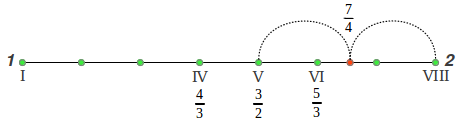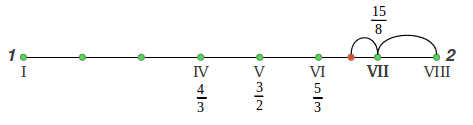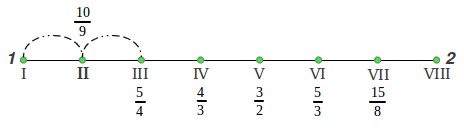- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Proporción en las escalas musicales
Tabla de Contenido
1.- Introducción
2.- La escala: intervalos y cocientes
3.- La escala "pitagórica"
3.1.- Deducción de la escala diatónica
3.2.- Tetracordes y las siete escalas
3.3.- Extension a la escala cromática: La espiral de quintas (o cuartas)
4.- La Lambda de Platón y las tres medias
5.- La escala del Temperamento Igual
6.- La escala de Intervalos Justos
6.1.- Deducción a partir de las medias aritmética y armónica
6.2.- Comparación de intervalos entre escalas
6.3.- Los intervalos de las escalas en el monocorde
7.- Los Modos Aulos griegos
7.1.- Antecedentes históricos
7.2.- Una forma alternativa de estudiar el monocorde
7.3.- Deducción a partir de la media armónica
7.4.- Los siete antiguos Modos griegos
7.5.- Los siete Modos griegos como subespecies
8.- La escala de Doce Quintas
8.1.- La estructura de la escala y las quintas formadas
8.2.- Acerca de la frecuencia de afinación correcta A=432Hz
9.- Referencias
1.- Introducción
Hace un tiempo, cuando reproduje y extendí parte de la investigación de Jean-Claude Perez sobre el ADN, encontré algunos intervalos musicales en diversos cocientes (ratios) de las poblaciones de codones del ADN del genoma humano completo (véase este artículo). Tratando de encontrar alguna explicación para estos hallazgos, como no tenía conocimientos musicales, empecé a estudiar la estructura de las escalas musicales. Había aprendido del excelente libro sobre Geometría Sagrada de Robert Lawlor que las escalas musicales están de alguna forma relacionadas con las media aritmética, geométrica y armónica, pero él no profundizaba más en el asunto. A parte de la más ámpliamente conocida Escala del Temperamento Igual, también me sentí atraído por el comunmente conocido cómo sistema de afinación "Pitagórica". Para mi sorpresa, descubrí que este sistema de afinación no era el que usaba realmente la Escuela Pitágorica (fué introducido con posterioridad por Aristógeno). La música pitagórica estaba basada muy probablemente en los antiguos Modos Aulós, redescubiertos y cuidadosamente documentados por Kathleen Schlesinger, cuidadora de instrumentos musicales antiguos del Museo Británico, después de darse cuenta de que los agujeros para los dedos de los aulós Griegos parecían ser equidistantes.
En la primera parte de este artículo introduciré los fundamentos matemáticos básicos que hay detrás de las escalas musicales, de forma que cualquiera sin conocimientos musicales como yo pueda entender su estructura. La mayoría de libros sobre teoría musical se focalizan en el proceso aritmético, pero la falta de un soporte gráfico dificulta su estudio. Para ayudar a comparar distintas escalas musicales y a entender su estructura de intervalos, introduzco un método gráfico sencillo basado en colores en el cual los intervalos están dibujados a escala. Ello simplifica enormemente su estudio, y espero que también pueda resultar de utilidad al músico experto. Si eres músico y encuentras algún error en mi exposición, por favor házmelo saber; confío en que la figura de abajo te deje con la curiosidad suficiente como para seguir leyendo... Voy a mostrar como la estructura de las escalas musicales, tanto actuales como antiguas, puede obtenerse fácilmente a partir de las tres medias matemáticas (aritmética, geométrica y armónica), y cómo la gran diversidad de intervalos musicales disponibles en los antiguos Modos Aulos Griegos se ha ido perdiendo gradualmente de la práctica musical común. Por último, explicaré la estructura de una nueva escala desarrollada por la violinista Maria Renold, la cual combina lo mejor de la antigua escala de Aristógeno y de la moderna Escala del Temperamento Igual: la Escala de las Doce Quintas. Ello nos permitirá introducir el hecho de que tanto la estructura de una escala como la frecuencia a la cual está afinada tienen efectos diferentes sobre el ser humano, algo que sospecho puede estar relacionado con la estructura geométrica del sonido en el espacio tridimensional. Este tema se discutirá más a fondo en la segunda parte del artículo.
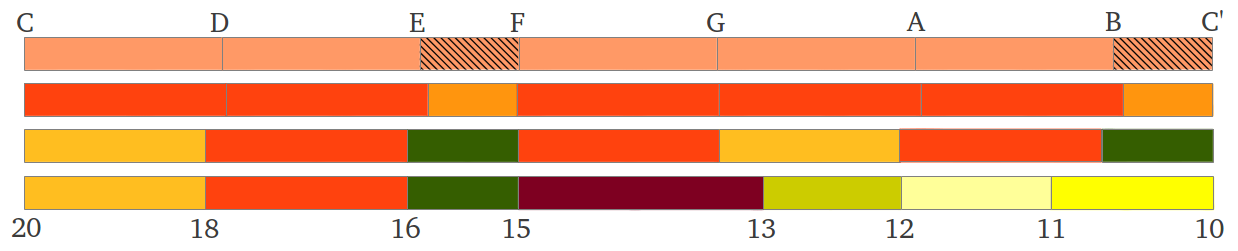
Escalas Diatónicas antiguas y modernas comparadas
2.- La escala: intervalos y cocientes
El intervalo musical báscio es la octava, la cual contiene un número infinito de frecuencias entre una frecuencia de referencia (la tónica) y su doble. La escalas particionan el continuo de una octava en diversas porciones conocidas como intervalos. A medida que una pieza musical progresa, usa intervalos y combinaciones de intervalos (acordes) de este subconjunto predefinido. La estructura de una escala determinada es la misma en todas las octavas. el número de intervalos así como la longitud de cada intervalo en una escala suelen estar determinados culturalmente. No obstante, el conjunto de todas las posibles notas por octava habitualmente se reduce a un número muy reducido: siete notas en nuestra escala diatónica, pero hasta 22 notas por octava en algunas tradiciones indias, arábigas o turcas [1]. Maria Renold destaca la octava y la escala como sigue [2]:
"La octava es un intervalo excepcionalmente importante en la experiencia musical de la humanidad occidental. Muchas escalas están contenidas dentro de la octava, y todos los intervalos, que buscamos entender aquí, están contenidos en esas escalas. Cada escala que progresa de la nota clave o tónica hasta la octava, tanto si es ascendente como descendente, la mayoría de la gente la oye coomo un todo orgánico -con una audición cuidadosa, hasta la escala cromática de doce notas. Por lo tanto la estructura completa de intervalos de una escala puede considerarse una estructura orgánica con sus propias leyes que procede de la octava."
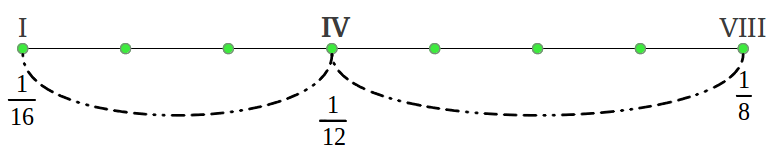
Las siete notas en la escala diatónica, que se corresponden con las siete teclas blancas del piano, a menudo se numeran con cifras romanas según su posición, desde la primera nota o tónica (DO=I) pasando por la séptima nota (SI=VII) hasta la octava nota (DO=VIII) que también es la primera nota de la siguiente octava:

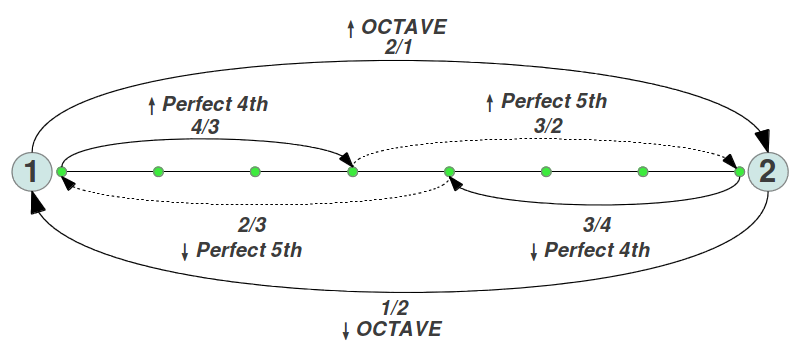
La longitud de un intervalo comprendido entre dos notas de frecuencias f1 y f2 se mide por su cociente (ratio) f2/f1. La cuarta nota (FA=IV) se dice que forma un intervalo de una Cuarta con la primera nota (DO=I). Si el cociente de frecuencias de estas dos notas es exactamente 4/3, se dice que forman una 4ª Perfecta. De forma similar, la quinta nota (SOL=V) forma una 5ª Perfecta con la primera nota si su cociente es exactamente 3/2. Las cinco notas restantes desde una 4ª perfecta hasta la octava también forman un intervalo de una 5ª perfecta, porque 2/(4/3) = 3/2. Así pues, la octava se puede dividir de forma exacta en dos intervalos de una 4ª perfecta y una 5ª perfecta (Figura 1). Los intervalos también pueden formarse en orden descendente (como las notas pueden tocarse de igual forma), y en este caso los cocientes entre sus frecuencias correspondientes será un número comprendido entre 1/2 y 1, por ejemplo 2/3 para una 5ª perfecta descendiente, y 3/4 para una 4ª perfecta descendiente (Figura 1). Las notas en una octava siempre se pueden representar mediante números comprendidos entre 1 y 2, siempre que normalicemos la frecuencia de todas las notas con respecto a la tónica (primera nota). A pesar de que las figura de arriba y de abajo puedan sugerir lo contrario, la longitud de cada intervalo individual de la escala diatónica no es la misma. En breve introduciremos un método gráfico para representar cada intervalo a escala, pero primero necesitamos introducir la medida de un intervalo en cents.
|
|
|
| Figura 1: Una octava siempre se puede representar mediante números comprendidos entre 1 y 2 siempre que las frecuqencias de todas sus notas se normalicen respecto a la frecuencia de la primera nota. La octava se puede dividir de forma exacta en dos intervalos de una 4ª perfecta y una 5ª perfecta, tanto descendiente como ascendiente. | |
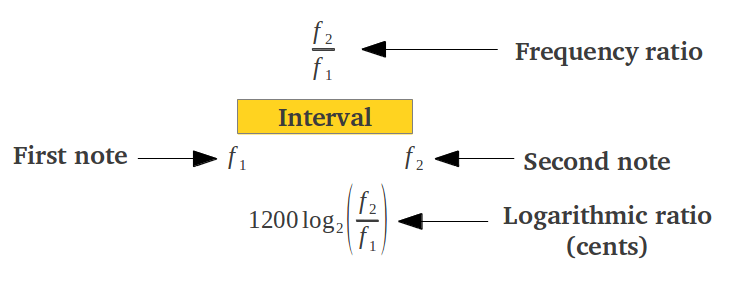
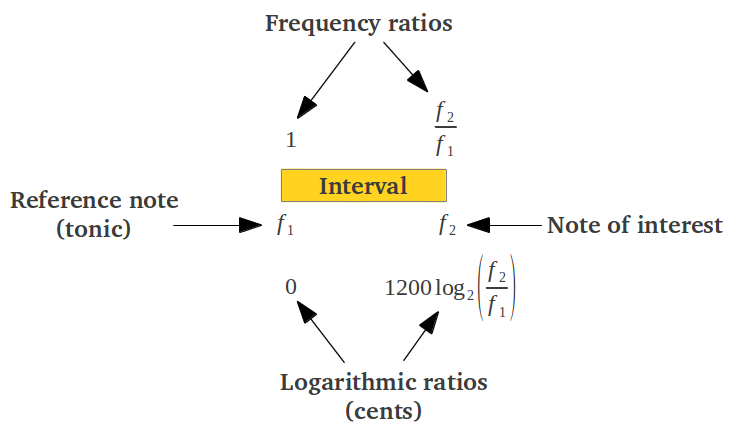
Trabajar con cociente enteros no resulta cómodo porque se tiene que operar de forma multiplicativa. Por ejemplo para conseguir el intervalo de una octava a partir de una 4ª perfecta y una 5ª perfecta, se tienen que multiplicar los cocientes individuales: (4/3) x (3/2) = 2. Además, los intervalos musicales que se usan en la moderna Escala del Temperamento Igual no son cocientes enteros exactos entre sus frecuencias correspondientes. Los teóricos de música han desarrollado un método alternativo para representar un intervalo que se comporta de forma aditiva y utiliza números reales. La función matemática que convierte el producto en suma de forma natural es el logaritmo, ya que log(ab) = log(a) + log(b) y log(b/a) = log(b) - log(a). Un intervalo f2/f1 a menudo se expresa en Cents según la fórmula 1200·log2(f2/f1). De esta forma, una octava ocupa exactamente 1200 cents (Figura 2a). Resulta habitual normalizar todos los intervalos de una octava respecto a la tónica (Figura 2b).
|
(a) |
(b) |
| Figura 2: Representación alternativa de un intervalo musical como un cociente lineal o en cents logarítmicos, tanto de forma (a) direca o (b) normalizada. | |
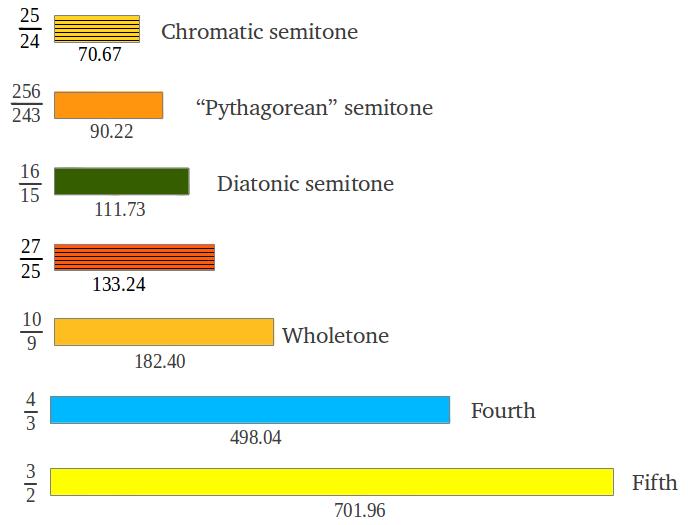
La figura siguiente muestra diversos ejemplos de intervalos encontrados en la práctica musical comúm, como cocientes enteros y en cents. De ahora en adelante, todos los intervalos se dibujarán a escala, con una longitud proporcional al valor del intervalo en cents. Ello proporciona una forma sencilla de sumar y comparar intervalos de forma gráfica.
 |
||
| Figura 3: Ejemplos de algunos intervalos musicales comunes. La longitud de cada intervalo se ha dibujado a escala, de forma proporcional a su valor en cents. |
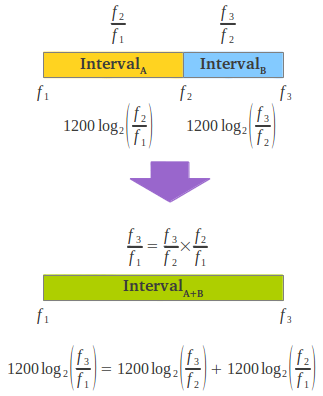
Si se unen dos intervalos, el cociente del intervalo resultante es el producto de los cocientes de cada intervalo constituyente. La representación logarítmica de los intervalos musicales traduce la multiplicación de cocientes en suma de cents (Figura 4). Siguiendo nuestra representación gráfica, para obtener el resultado de la suma de dos intervalos tan sólo se necesita ponerlos uno a continuación del otro. La Figura 4b contiene ejemplos de suma de algunos de los intervalos mostrados en la Figura 3 de arriba.
|
(a) |
(b) |
| Figura 4: Tres notas definen dos intervalos musicales que se pueden unir operando de forma multiplicativa o de forma aditiva en cents. | |
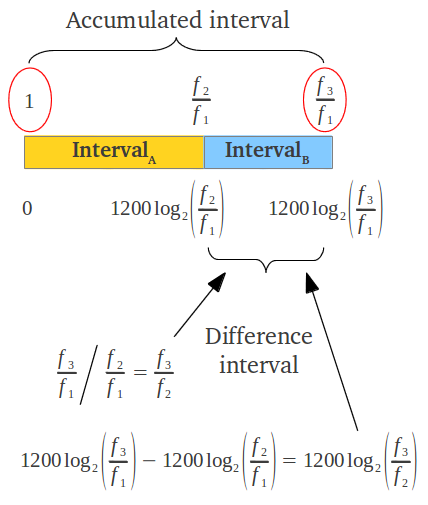
Cuando se necesita dibujar más de un intervalo simultáneamente, como sucede cuando estamos representando las siete notas de una escala diatónica, resulta habitual sustituir cada nota por el intervalo acumulado desde la tónica hasta esa nota. Esta operación equivale a normalizar (dividir) la frecuencia de cada nota por la frecuencia de la tónica (Figura 5a). En ese tipo de representación, el cociente de cualquiera de los intervalos individuales (intervalos entre notas consecutivas) puede obtenerse dividiendo los cocientes acumulados de las dos notas que forman el intervalo, o alternativamente restando sus valores equivalentes en cents (Figura 5).
|
(a) |
(b) |
| Figura 5: Cada nota en una representación conjunta de diversos intervalos normalmente se normaliza con respecto a la tónica. Por lo tanto el cociente correspondiente representa el intervalo acumulado desde la tónica hasta esa nota. Cualquiera de los intervalos individuales (entre dos notas consecutivas) puede calcularse o bien dividiendo los cocientes correspondientes, o bien restando sus valores equivalentes en cents. | |
3.- La escala "Pitagórica"
3.1.- Deducción de la escala diatónica
La escala griega de site notas que ha sobrevivido de forma escrita estaba basada en quintas y cuartas perfectas. Esta escala se conoce en todas partes como afinamiento "Pitagórico", pero en realidad fue introducido por Aristógeno de la escuela de los Teoristas en sus 12 polémicas, un ataque escrito al sistema musical pitagórico. Pitágoras y sus discípulos, que eran conocidos como los Harmonistas, en realidad usaban los siete Modos Aulos descritos en una sección posterior [3]. Por lo tanto, la escala griega basada en cuartas y quintas perfectas que vamos a describir debería llamarse en realidad escala Aristogeniana. La premisa básica de esta escala es que contenga tantas cuartas y quintas perfectas como sea posible. Más adelante mostraré un antiguo método chino que permite calcular las escalas "pitagóricas" de cinco notas (pentatónica) y de siete notas (heptatónica), ambas carentes de la última nota: la octava.
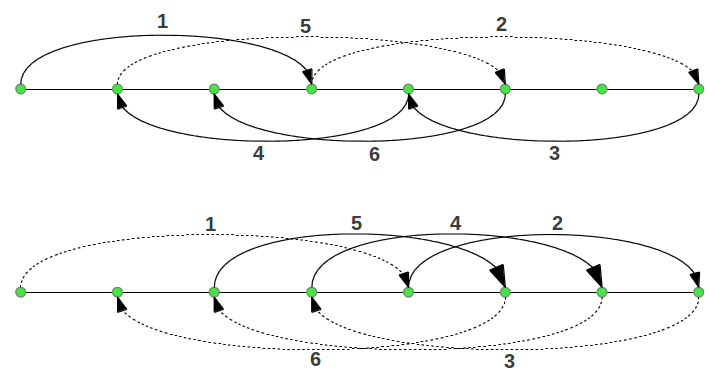
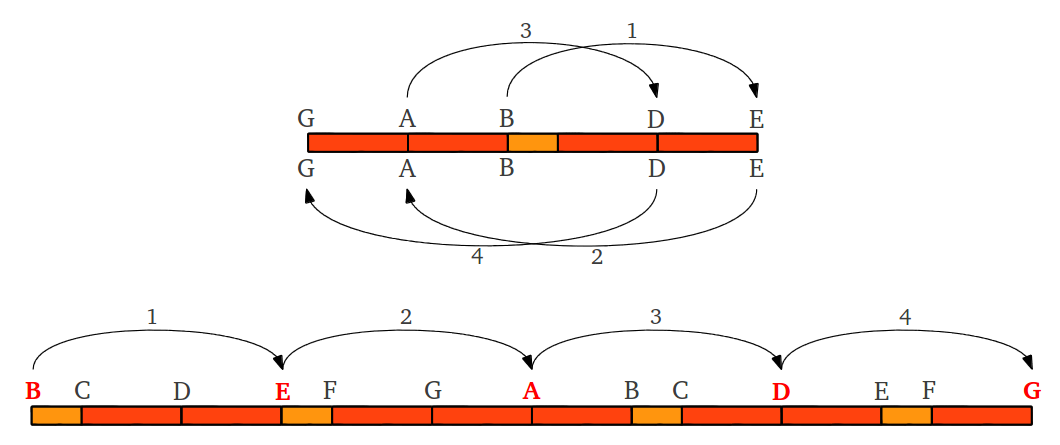
La longitud de todos los intervalos en esta escala, incluyendo la octava, pueden obtenerse fácilmente usando seis "saltos" alternativos de una cuarta perfecta (un intervalo de cuatro notas con un cociente de 4/3) o una quinta perfecta (un intervalo de cinco notas con un cociente de 3/2), de forma ascendente o descendente según convenga, dependiendo de la nota en la que queramos "aterrizar". La Figura 6 muestra dos alternativas diferentes de efectuar esos saltos para completar las ocho notas de la escala.
|
|
|
| Figura 6: Dos formas posibles de obtener las ocho notas de la escala "pitagórica" mediante saltos alternativos de una cuarta o una quinta perfecta, ya sea de forma ascendente o descendente. |
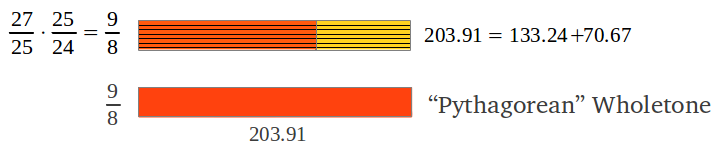
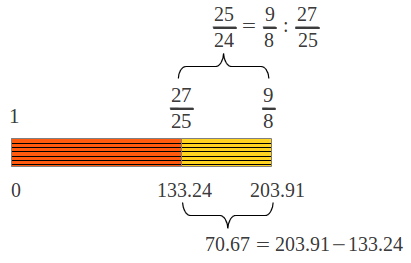
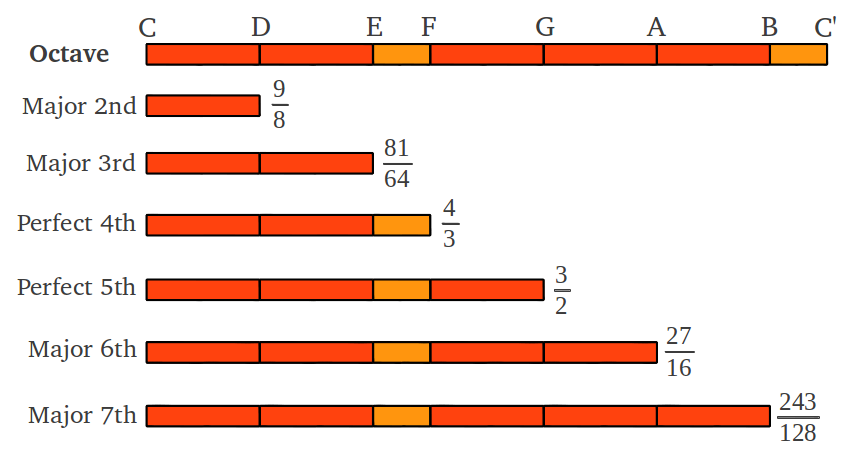
Cada salto proporciona el cociente acumulado desde la tónica hasta la nota de "aterrizaje" multiplicando los cocientes correspondientes (como se describe en la Figura 1 de arriba). Por ejemplo si seguimos la primera secuencia de saltos, la séptima nota se alcanza en el paso 4, y su cociente es (4/3)·(4/3) = 16/9. El resultado final despues de los seis pasos de la primera secuencia se muestra en la Figura 7a. ¿Cuántos intervalos individuales distintos hay en esta escala? Para calcular la longitud de cada intervalo individual hay que dividir sus cocientes acumulados. El resultado sorprendente es que hay tan sólo dos longitudes de intervalo diferentes como se muestra en la Figura 7b: la de un tono completo "pitagórico" (9/8 o 203.91 cents, véase la Figura 4b), y la de un semitono "pitagórico" (243/128 o 90.22 cents, Figura 3). El semitono "pitagórico" es menor (en el argot musical más llano) que medio tono completo. La Figura 7c muestra los nombres comúnmente aceptados para las siete notas de la escala diatónica (que también pueden verse como intervalos acumulados respecto a la tónica).
|
(a) |
|
|
(b) |
|
 (c) (c) |
|
| Figura 7: (a) El cociente acumulado de cada nota en la escala "Pitagórica" obtenida después de la primera secuencia de seis pasos que se detalla en la Figura 6. (b) Esta escala contine sólo dos intervalos individuales distintos. (c) Los nombres comunmente aceptados de cada nota de la escala diatónica; cada nota puede verse también como un intervalo acumulado desde la tónica. |
Resulta importante observar que no todos los intervalos de cuatro notas consecutivas forman una cuarta perfecta. La cuarta perfecta contiene dos tonos completos "pitagóricos" y un semitono. Cualquier combinación de dos tonos completos más un semitono es una cuarta, pero no será perfecta (cociente exacto de 4/3 o 498.04 cents) si varía la longitud de cualquiera de sus constituyentes: por ejemplo si uno de los tonos completos se reduce a 10/9 como sucede en la Escala de los Intervalos Justos (véase más adelante). De forma similar, una 5ª perfecta contiene exactamente tres tonos completos "pitagóricos" más un semitono "pitagórico" (cociente exacto de 3/2 o 701.96 cents).
3.2.- Tetracordes y las siete escalas
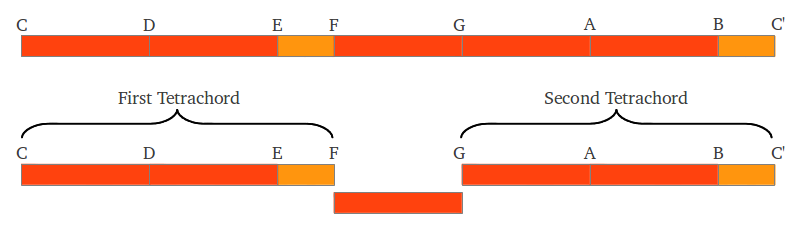
En la figura precedente hemos introducido otra notación habitual en la práctica musical, en la cual a cada nota se le asigna una letra del conjunto A-G. La asignación no es aleatoria: se hace de tal forma que el intervalo E-F sea el semitono ubicado después de dos tonos completos consecutivos, y el intervalo B-C' es el semitono que sigue a tres tonos completos consecutivos. La estructura de esta escala griega fue originalmente dividida por Aristógeno en dos tetracordes separados por en medio por un tono completo (Figura 8).
 |
|
| Figura 8: Escala C "pitagórica" como dos tetracordes. |
¿Qué habría sucedido si hubiéramos utilizado el segundo conjunto de seis pasos de la Figura 6? Procediendo como arriba, el lector puede comprobar que el resultado final sería el que se muestra en la Figura 9. El número total de tonos completos y semitonos es el mismo, pero con una distribución distinta. La secuencia de intervalos es la misma, pero empieza en un semitono "pitagórico" seguido por tres tonos completos, por lo tanto se llama Escala E.
|
(a) |
|
|
(b) |
|
| Figura 9: (a) El cociente acumulado de cada nota en la escala "pitagórica" después de la segunda secuencia de seis pasos detallada en la Figura 6. (b) La secuencia de intervalos empieza en la nota E. |
Puede apreciarse que la escala E de la Figura 8b es en ralidad un "desplazamiento circular" de la escala C mostrada en la Figura 9b. De hecho, si dibujamos dos octavas consecutivas podemos ver fácilmente que en realidad existen siete escalas "pitagóricas" distintas, dependiendo de la nota en que empiece la escala (Figura 10).
 |
|
| Figura 10: En realidad hay siete escalas o modos en la escala diatónica "pitagórica", según en qué nota empiece la escala. |
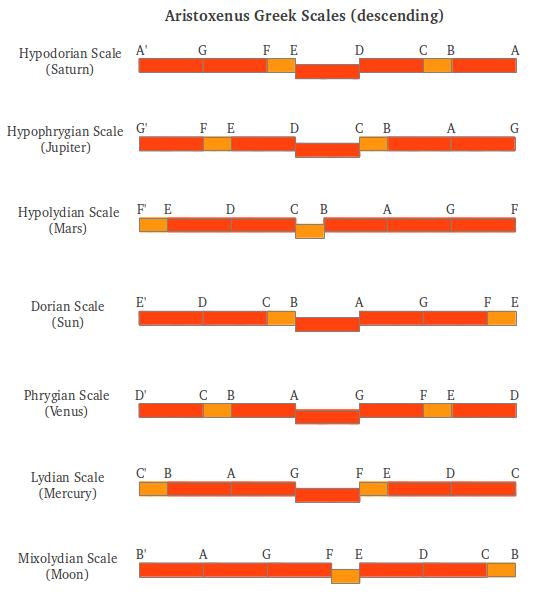
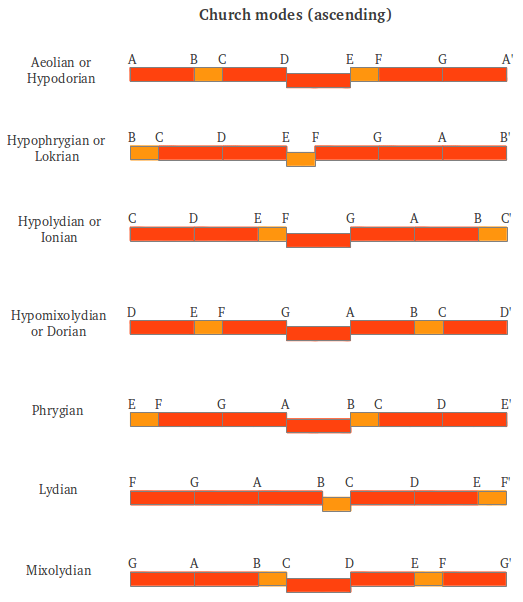
Estas siete escalas, originalmente descritas por Aristógeno en orden descendente, también se llamaban modos, pero no deben confundirse con los antiguos Modos Aulós griegos que tratamos en una sección posterior. Cada escala estaba asociada a un planeta distinto según Nicómaco, y también según la visión del mundo Ptolomea (Figura 11a). Los nombres originales de les siete escalas griegas se convirtieron posteriormente en los modos ascendentes eclesiásticos y sus nombres de mezclaron por error (Figura 11b).
 |
 |
|
|
Figura 11: Las siete escalas griegas descendientes, su asociación a los planetas y su posterior conversión en modos eclesiásticos [2]. |
||
3.3.- Extensión a una escala cromática: La espiral de quintas (o cuartas)
Hasta ahora tan sólo hemos considerado la escala diatónica de siete notas, pero la mayor parte de la música occiental moderna utiliza una escala de doce notas conocida como escala cromática. ¿Es posible extender la escala "pitagórica" diatónica a una escala cromática? Para responder a esta pregunta, voy a servirme de un antiguo método chino para calcular la escala "pitagórica" pentatónica, que luego puede extenderse a una escala heptatónica y por último a una escala de doce notas. Este procedimiento se conoce en todas partes como "La espiral de quintas", aunque resulta mucho más fácil de entender si usamos el intervalo complementario de una cuarta.
La regla se conoce com "sumar o restar un tercio", y su expresión más antigua está atribuida a Kuan Tzu (siglo VII A.C.) el cual explica cómo aplicarla de froma aritmética y geométrica para generar la escala pentatónica [4]. Se tiene que empezar por "tres cuatro veces", es decir 3x3x3x3=34=81, y aplicar la regla hasta que las potencia de 3 se agoten. El primer paso sería 81+81·(1/3)=108=33·22; el segundo paso, 108-108·(1/3)=72=32·23; el tercer paso 72+72·(1/3)=96=3·25; y el cuarto y último paso 96-96·(1/3)=64=26. El lector se debe estar preguntando: ¿y la secuencia 81,108,72,96,64 qué tiene que ver con la música? Bien, cualquiera de esos números puede pensarse como una frecuencia, luego para saber cómo están ubicados en una escala musical -o cómo están separados por intervalos- necesitamos calcular sus cocientes. Normalizando por número menor 64 y reordenando obtenemos 1, 9/8, 81/64, 3/2, 27/16. ¿Resultan familiares estos cocientes? Si nos fijamos de nuevo en la Figura 7, podemos ver que en la escala C corresponden a la secuencia de notas C,D,E,G,A. En realidad, la primera nota es la tónica o nota de referencia, y los cuatro cocientes siguientes son intervalos: C-D (2ª Mayor), C-E (3ª Mayor), C-G (5ª Perfecta) y C-A (6ª Mayor). Observando la Figura 10, podemos ver que la escala G comparte con la escala C la misma estructura de intervalos inicial. En la escala G la secuencia de enteros 64,72,81,96,108 representa las notas G,A,C,D,E. Ambas escalas nos proporcionan la misma secuencia cíclica de cinco notas, las cuales forman la antigua escala pentatónica. Obsérvese que cualquier otra permutación cíclica de esas notas también serviría (D,E,G,A,C; E,G,A,C,D; o A,C,D,E,G).
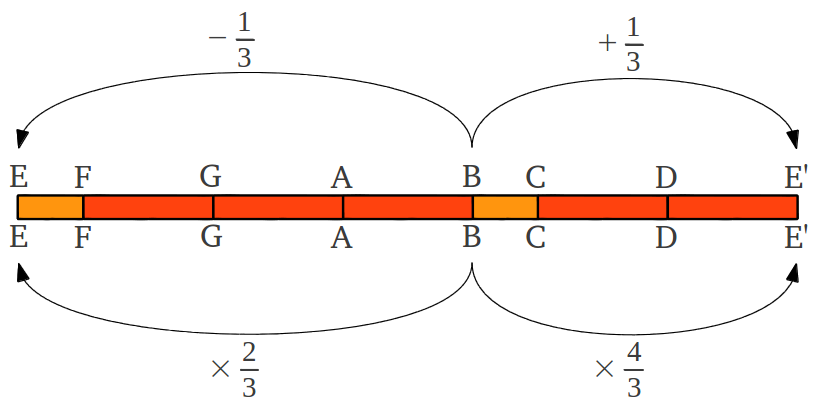
El proceso completo se entiende mejor de forma gráfica (Figura 12). Sumar un tercio en realidad significa ascender una cuarta perfecta (4/3 = 1 + 1/3), mientras que restar un tercio es equivalente a descender una quinta perfecta (2/3 = 1 - 1/3). La secuencia de notas G,A,C,D,E puede obtenerse empezando por la nota B y efectuando los cuatro pasos alternados de +1/3, -1/3, +1/3, -1/3 (Figura 12b).
|
(a) |
|
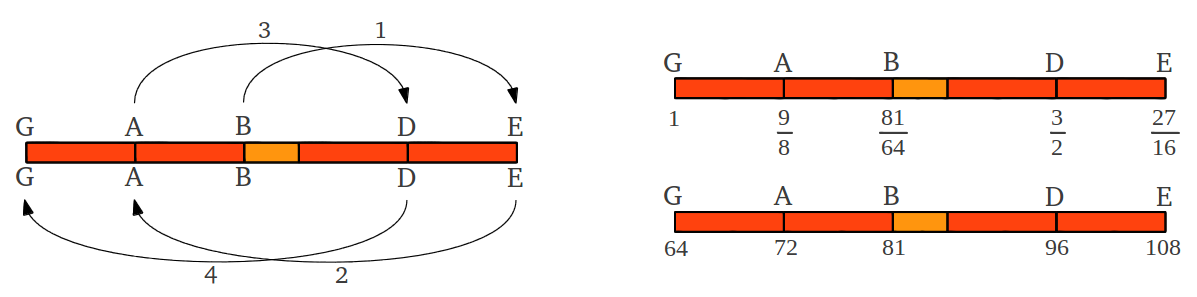 (b) (b) |
|
| Figura 12: (a) La antigua regla "sumar o restar un tercio" en realidad es equivalente a ascender una 4ª perfecta o descender una 5ª perfecta. (b) La aplicación de la regla empezando en la nota B genera la antigua escala pentatónica G,A,B,D,E después de cuatro pasos, la cual puede representarse de forma numérica por la secuencia de números enteros 64,72,81,96,108. |
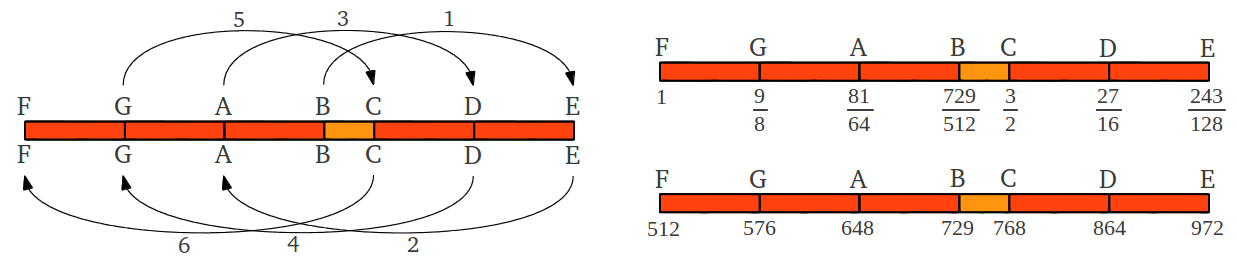
La regla simple de "sumar o restar un tercio" puede extenderse dos pasos más hasta generar la escala heptatónica, también conocida como el heptacorde de Terpander (Figura 13).
 |
|
| Figura 13: Aplicación de la regla empezando en la nota B genera la escala heptatónica F,G,A,B,C,D,E después de seis pasos. Esta escala puede representarse de forma numérica mediante la secuencia de enteros 512,576,648,729,768,864,972. |
La escala heptatónica contiene todos los intervalos internos de la escala "pitagórica" diatónica ¡¡excepto la octava!! Esta es una limitación conocida del proceso de obtención de las notas exclusivamente a partir de cuartas (o quintas). De hecho, descender una quinta en realidad es equivalente a ascender una cuarta y trasladar la nota resultante a la primera octava dividiendo por 2. Por lo tanto, los saltos alternativos de más/menos un tercio pueden sustituirse por saltos positivos de +1/3 (ascender una 4ª perfecta) seguidos de la división por la potencia de 2 adecuada. Esto se ilustra en la Figura 14 en el proceso de cuatro pasos que genera la escala pentatónica.
|
|
|
| Figura 14: Descender una quinta en realidad es equivalente a ascender una cuarta y trasladar hacia abajo a la primera octava. |
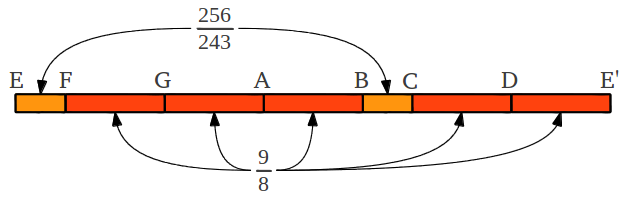
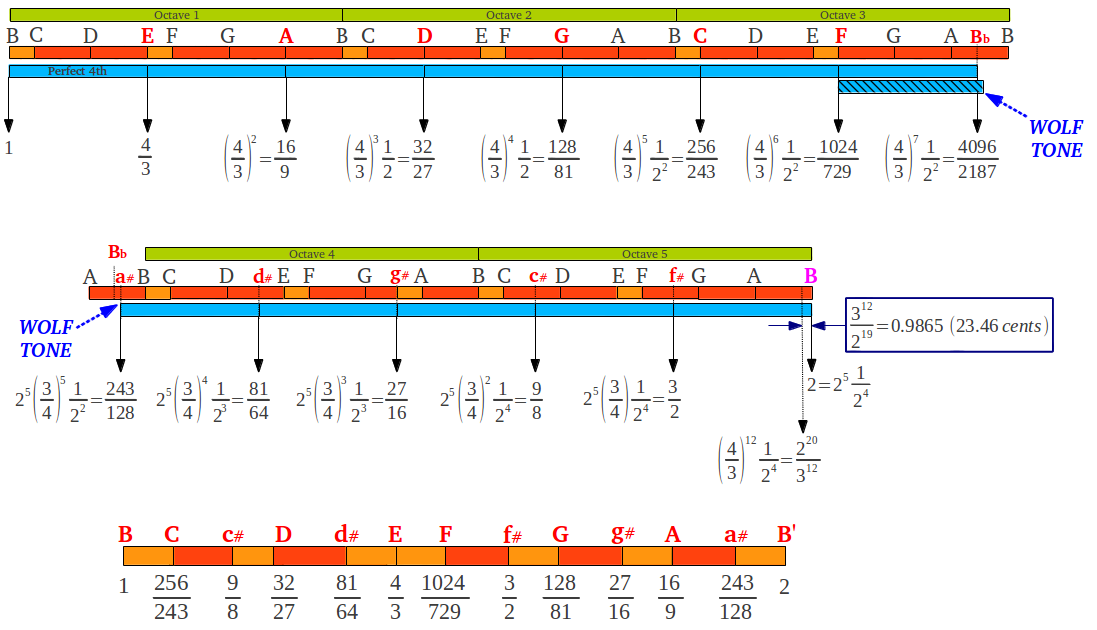
Para obtener las doce notas de la escala cromática, este proceso puede iterarse doce veces. No obstante, después del sexto paso se observa que los cocientes obtenidos testán formados por cifras cada vez mayores, y que el proceso final no acaba en una octava perfecta. Para superar este problema, la cuarta número 7 puede alargarse ligeramente dando lugar a lo que se conoce como el tono "lobo", y esto hace posible continuar con cuartas perfectas y alcanzar una octava perfecta en el doceavo paso (Figura 15). El error entre la quinta octava perfecta y la que se alcanza después de 12 cuartas perfectas se conoce como la coma "pitagórica" (23.46 cents).
|
|
|
| Figura 15: Proceso de obtención de la escala cromática "pitagórica" a partir de una secuencia de cuartas. Para llegar a la quinta octava sin el error de una coma "pitagórica" (23.46 cents), la cuarta número 7 se alarga ligeramente dando lugar al tono "lobo" en la nota a#. El resultado es la escala cromática "pitagórica" en el modo B. |
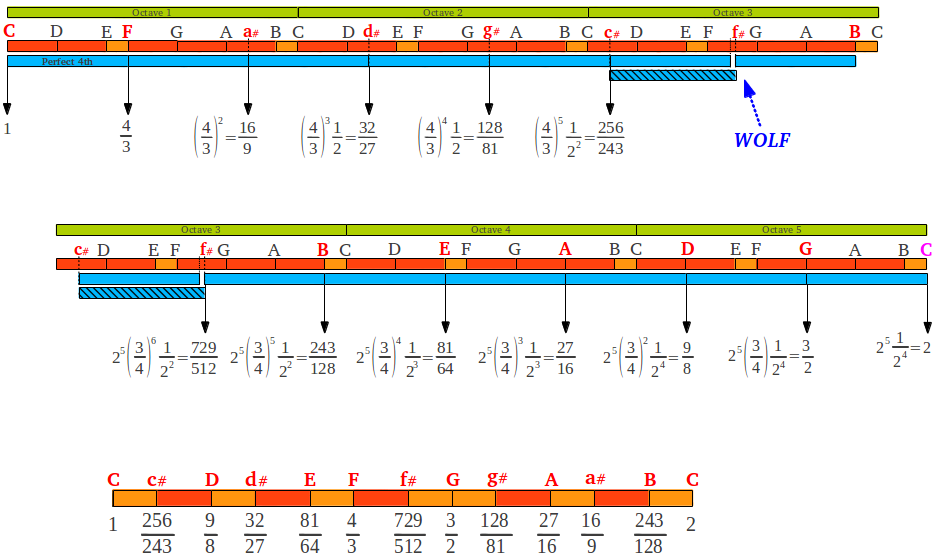
El tono "lobo" puede caer en notas distintas, dependiendo de la nota en la que se empiece el proceso. En la figura siguiente mostramos el mismo proceso empezando por la nota C más familiar. En este caso el tono "lobo" aparece en la nota f#.
|
|
|
| Figura 17: La escala "pitagórica" cromática en el modo C, con el tono "lobo" ubicado en la nota f#. |
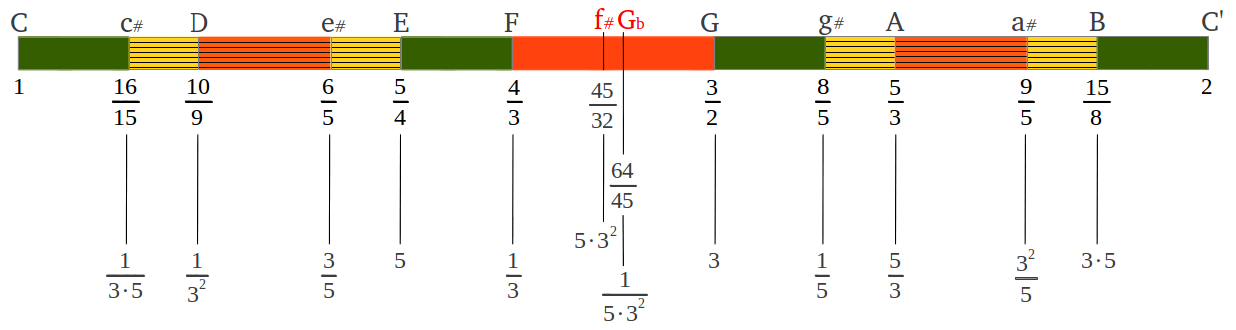
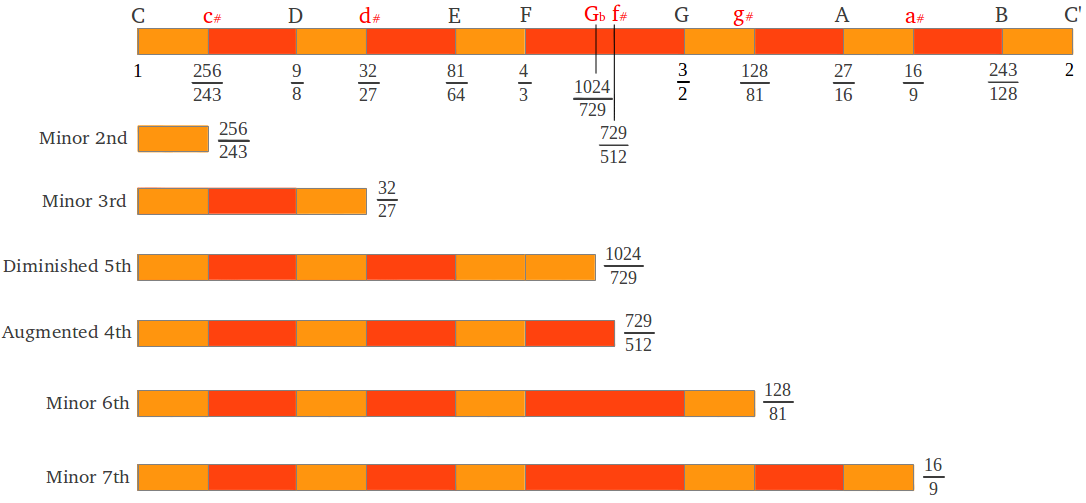
Las cinco nuevas notas obtenidas corresponderían a las teclas negras del piano. Sus nombres estándar se muestran en la Figura 18, donde también podemos ver sus correspondientes intervalos con respecto a la tónica C. Para hacer la figura completa, mostramos los dos posibles valores del tono "lobo": la cuarta aumentada o la quinta disminuida. En la escala C corresponden con las dos aproximaciones "pitagóricas" del tritono, una nota ubicada exactamente en el medio de la Escala del Temperamento Igual (véase sección posterior).
 |
|
| Figura 18: Las cinco notas adicionales de la escala C cromática "pitagórica". |
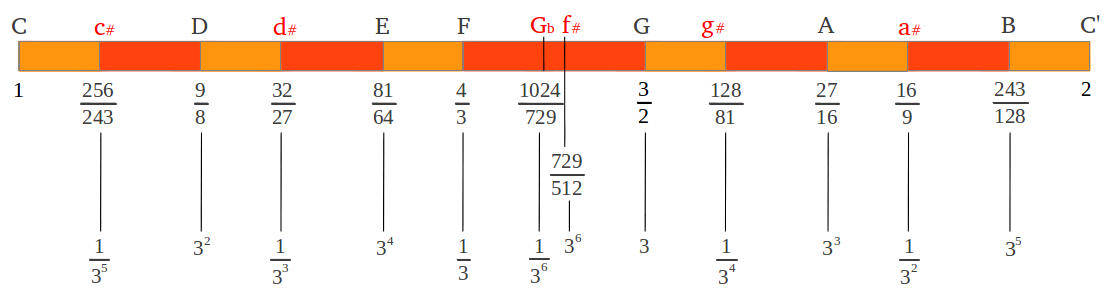
Por último, no querría terminar el estudio de la escala "pitagórica" sin destacar la importancia del número 3 en esta escala. Si analizamos detenidamente los cocientes contenidos en los intervalos de esta escala, podemos ver que están todos basados en potencias de 3. Dada una determinada potencia de 3, ya sea positiva o negativa, el número 2 actúa como un comodín que nos permite trasladarla a la octava 1-2, convirtiendo así un valor entero en una fracción comprendida entre 1 y 2. La Figura 19 resume este análisis.
 |
|
| Figura 19: Los doce intervalos de la escala cromática "pitagórica" como potencias de 3. |
4.- La Lambda de Platón y las tres medias
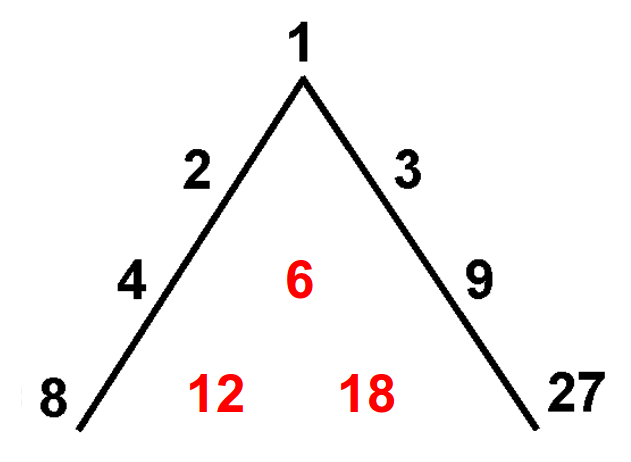
La famosa disposición de las tres primeras potencias de los números 2 y 3 conocida como la Lambda de Platón (Figura 20a) nos ayudará a introducir las tres medias (aritmética, geométrica y armónica) en las escalas musicales. Los números en negro de la Lambda original siguen unaprogresión geométrica, luego cada número es la media geométrica entre su número precedente y el siguiente (por ejemplo 9=32 es la media geométrica entre 3=31 y 27=33). La Lambda "completa" contiene también los números rojos de enmedio (6, 8 y 12) los cuales pueden obtenerse fácilmente a partir de sus vecinos mediante la media aritmética y armónica. La Figura 20b nos recuerda cómo calcular las tres medias y cómo están relacionada entre sí.
|
(a) La Lambda de Platón |
(b) La tres medias |
| Figura 20: Los números en negro en la Lambda de Platón (a la izquierda) siguen una progresión geométrica, luego cada uno es la Media Geométrica (GM) entre los números precedente y siguiente. Los números en rojo pueden obtenerse a través de la Media Aritmética (AM) y la Media Armónica (HM) definidas en la derecha. | |
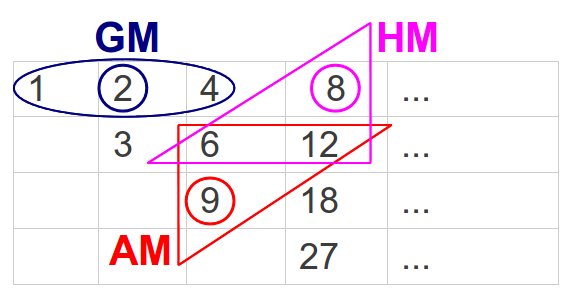
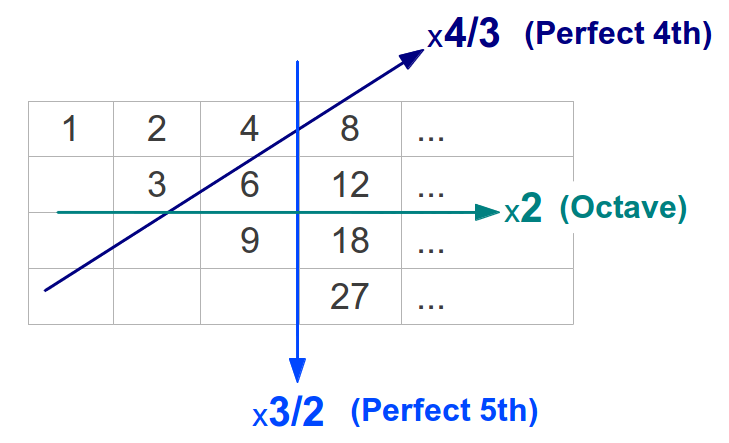
La relación entre tods estos números y las tres medias se entiende mejor si se reagrupan en lo que se conoce como la Tabla de Nicómaco (Figura 21a). Cada número en una fila dobla su predecesor; eso es así tanto en la primera fila (potencias de 2) como en todas las demás. Cada número es la media aritmética de los dos números por encima de él, por ejemplo 9 = (6+12)/2, y la media armónica de los dos números por debajo de él, por ejemplo 8 = 2·6·12/(6+12). El lector probablemente se estará preguntando qué tiene todo esto que ver con los intervalos musicales: la explicació se encuentra en la Figura 21b. Allí podemos ver que los números de la Tabla de Nicómaco, tomados en la dirección apropiada, forman los intervalos de una octava (2), una 4ª perfecta (4/3), y una 5ª perfecta (3/2).
|
(a) Tabla de Nicómaco |
(b) Intervalos musicales |
| Figura 21: (a) Los números de la Lambda de Platón pueden reorganizarse en forma de una tabla también conocida como Tabla de Nicómaco. Cada número de la tabla puede obtenerse como la media geométrica, aritmética o armónica de dos números de su alrededor. (b) Los números de la tabla de Nicómacotambién están relacionados a través de los intervalos musicales más básicos de una 4ª perfecta (4/3), una 5ª perfecta (3/2) y una octava (2). | |
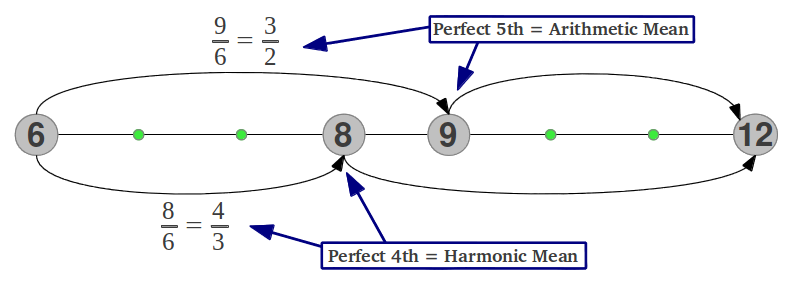
Consideremos que cada número de las tablas superiores representa la frecuencia de una nota. Los números 6 y 12 forman una octava. La nota inferior de la octava se suele llamar tónica. Los números 8 y 9 están contenidos en esta octava. El número 8 forma un intervalo de una 4ª perfecta con la tónica 6 puesto que forman el cociente 8/6 = 4/3, y el número 9 forma una 5ª perfecta con la tónica porue 9/6=3/2. El hecho interesante es que la 4ª perfecta (en este ejemplo 8) es la media armónica de los dos extremos de la octava (6 y 12), y la 5ª perfecta (en este caso 9) es su media aritmética. Eston son los dos pilares de la escala "pitagórica" discutida en la sección previa. La Figura 22 ilustra este hecho. En las secciones siguientes voy a mostrar cómo estas dos medias son también el corazón tanto de la Escala de los Intervalos Justos cómo de los antiguos Modos Aulós griegos.
 |
|
| Figura 22: 4ª perfecta (media armónica) y 5ª perfecta (media aritmética) |
5.- La escala del Temperamento Igual
Antes de entrar en la descripción y la estructura de las escalas de Intervalos Justos tanto antiguas como más recientes, vamos a introducir la escala moderna de 12 notas del Temperamento Igual (también llamada 12-tet), la cual es el sistema de afinación utilizado hoy en día en la mayoría de pianos. Esta escala habitualmente se da por supuesta de uso universal en los intrumentos de teclado, pero resulta importante saber que no existía en la práctica musical común con instrumentos hasta principios del siglo XX. Según William Sethares [1] "muchos músicos y compositores occidentales modernos incluso desconocen que existen alternativas. Esto no sorprende, ya que la mayoría de libros sobre escalas y harmonía musical se focalizan exclusivamente en el 12-tet, y muchas escuelas musicales ofrecen pocos cursos sobre música fuera del 12-tet, a pesar de que una porción significativa del repertorio musical histórico fuera escrito antes de que el 12-tet fuese común".
La idea del Temperamento Igual es muy simple: se fuerza que las 12 notas de la escala cromática suenen separadas una misma distancia. Es decir, la escala se divide en 12 semitonos iguales. Si el semitono tiene un cociente S y queremos alcanzar la octava después de 12 semitonos, la ecuación que se debe resolver es S12=2, de la cual el cociente de frecuencias de cada semitono tiene que ser la raíz doceava de dos, S=21/12=1.05946... Por lo tanto el cociente de frecuencias entre notas sucesivas ya no resulta una fracción (número racional) sino un número real, irracional. En el dominio logarítmico la longitud de un semitono es exactamente 1200·log2(21/12)=(1200/12)·log2(2)=100 cents. Siguiendo nuestra notación gráfica, la Figura 23 muestra la escala 12-tet así como la escala diatónica que contiene en su interior:
 |
|
| Figura 23: La escala del Temperamento Igual diatónica y cromática. |
Tan sólo tres de las doc notas de la escala 12-tet están relacionadas con una de las medias introducidas en la sección previa. Se pueden deducir fácilmente si uno se da cuenta de que la media geométrica de dos intervalos es equivalente a la media aritmética de sus valores correspondientes en cents. Así pues, si dividimos la octava en dos mitades (en cents) obtenemos el tritono, y si volvemos a dividir por dos cada una de las dos mitades, obtenemos la 3ª Menor y la 6ª Mayor. A partir de aquí se necesita dividir cada nuevo intervalo en tres partes para obtener las ocho notas restantes, lo cual equivale a realizar la raíz cúbica en el dominio lineal. Según Maria Renold "esto puede explicar por qué la calidad de los doce intervalos de esta escala es completamente diferente. Los tritonos, terceras menores y sextas mayores se experimentan como genuinas, mientras que las quintas, cuartas, terceras mayores, sextas menores segundas mayores y las dos séptimas suenan falsas [..] es decir falsificadas al oido humano. Este hecho es comunmente reconocido [2, p.43]."
6.- La escala de Intervalos Justos
6.1.- Deducción a partir de las medias aritmética y armónica
Una crítica de la escala del Temperamento Igual es que ninguno de sus intervalos es puro, ninguno se obtiene como un cociente exacto entre dos frecuencias. Por ejemplo las quintas miden 700 cents, mientras que una quinta perfecta (cociente 3/2) mide 702 cents. En esta escala, la imperfección del tono lobo se ha repartido por igual entre todas las quintas. La escala de Intervalos Justos puede definirse como el equivalente de la escala 12-tet pero compuesta de intervalos puros, basados en enteros. Esos intervalos tienen cociente de enteros pequeños y por ello suenan consonantes al oido. La gente encuentra más agradables los intervalos basados en cocientes de enteros pequeños porque el oído prefiere cocientes pequeños de forma natural. Galileo lo explicó de la siguiente forma [1, p.79]:
"Las consonancias agradables son pares de tonos que golpean el oído con una cierta regularidad; esta regularidad consiste en el hecho que los pulsos entregados por los dos tonos, en el mismo intervalo de tiempo, han de ser conmensurables en número, para no mantener el tímpano en un tormento perpetuo, doblándose en dos direcciones distintas cediendo a los impulsos contínuamente discordantes".
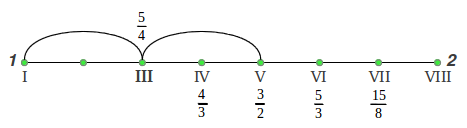
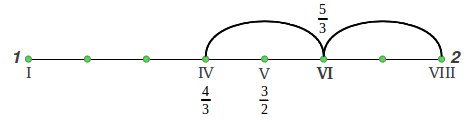
Pero ¿Cuáles son los valores precisos de esos cocientes exactos? No debería sorprendernos saber que, tal como sucedió con la 4ª y la 5ª perfectas, estos también se pueden deducir a partir de las medias aritmética y armónica dentro de la octava, como muestra Maria Renold en el capítulo 7 de su excelente libro bajo el título "Los principios de forma de las escalas Justas" [2]. El proceso se ilustra de forma gráfica en la Figura 24. Como ya sabemos de la sección 4 (Figura 24a), la media aritmética de una octava ascendente 1-2 es la 5ª perfecta (3/2), mientras que su media armónica es la 4ª perfecta (4/3). Si continuamos estas divisiones, la media aritmética entre la cuarta y la octava nos da la sexta mayor justa 5/3 (Figura 24b). La media aritmética entre la quinta y la octava (Figura 24c) nos proporciona un tono intermedio que no se usa en la escala (7/4), cuya media aritmética con la octava da lugar a la séptima justa 15/8 (Figura 24d). La media aritmética entre la quinta y la tónica nos da la tercera mayor justa 5/4 (Figura 24e) y por último la media armónica entre esta última y la tónica proporciona la nota restante, la segunda mayor justa 10/9 (Figura 24f):
|
(a) |
|
(b) |
|
|
(c) |
|
|
(d) |
|
|
(e) |
|
|
(f) |
|
 |
|
| Figura 24: La estructura de la escala de Intervalos Justos se puede obtener a partir de las medias aritmética y armónica. |
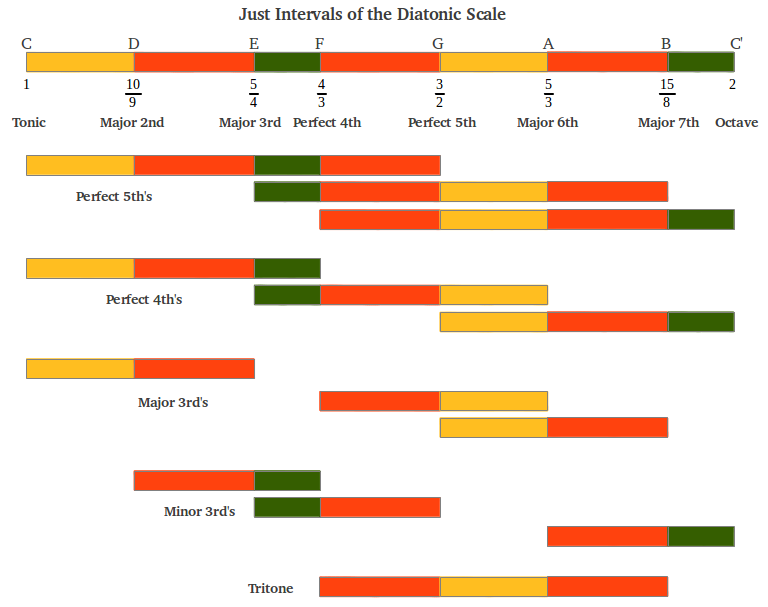
En la Figura 25 se muestra la longitud de los intervalos de la escala diatónica de Intervalos Justos proporcionalmente a sus valores en cents, así como los cocientes exactos de las notas de esta escala. Puede observarse que hay sólo tres intervalos individuales distintos en esta escala con cocientes 9/8, 10/9 and 16/15 (ver de nuevo las Figuras 3 y 4 anteriores). Existe una pequeña variante de esta escala en la cual los dos tonos completos del principio están intercambiados (en este caso, la segunda mayor resulta de la media aritmética en lugar de la media armónica entre la tercera mayor y la tónica).
 |
|
| Figura 25: Los Intervalos Justos de la escala diatónica. |
La escala que hemos obtenido en realidad se conoce en la práctica musical actual como Escala Mayor. Los músicos también usan una Escala Menor, que corresponde a un desplazamiento de la tónica a la nota A de forma que la tercera mayor se convierte en una tercera menor. La escala menor también se puede deducir a partir de las medias aritmética y armónica, pero no vamos a entrar en ese detalle aquí [2].
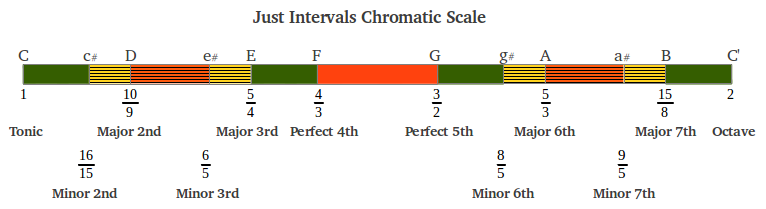
Se puede obtener una escala de Intervalos Justos cromática sumando o restando un semitono a las notas apropiadas de la escala diatónica de siete notas (Figura 26a). La escala resultante merece diversas consideraciones. Ante todo, resulta absolutamente simétrica, es decir tiene la misma secuencia de intervalos tanto ascendentes como descendentes. Esto también se puede observar en los cocientes de los intervalos: por ejemplo el intervalo simétrico de la tercera mayor (5/4) es la sexta menor (8/5) puesto que 2/(5/4) = 8/5. Ello también demuestra que estos dos intervalos son complementarios, es decir suman una octava, ya que (5/4)·(8/5) = 2. De forma similar, descender una tercera menor (6/5) nos situa en su simétrica ascendente, la sexta mayor en 2/(6/5) = 5/3.
También resulta interesante observar que la estructura de la escala de Intervalos Justos ha incorporado potencias del número 5 a las potencias del número 3 que se usaban de forma exclusiva en la escala de Aristógeno. Podemos apreciar en la Figura 26b que el número cinco sólo aparece elevado a la primera potencia, ya sea en el numerador o en el denominador, y que las potencia de tres se han reducido al segundo grado. Para hacerla autocontenida, también se han incluido en la figura las aproximaciones justas del tritono del temperamento igual, la cuarta aumentada y la quinta disminuida. Nótese la inversión que tiene lugar en comparación con esas mismas dos notas de la escala cromática "pitagórica" (ver Figura 19).
|
(a) |
|
|
(b) |
|
| Figura 26: Escala cromática de Intervalos Justos en base a potencias de 3 y 5. |
Los intervalos justos contenidos en esta escala se muestran en la Figura 27. Está claro que esta escala cromática contiene muchos intervalos puros en su interior. Por el contrario, esta figura nos permite ver una limitación inherente de esta escala, en lo que respecta a la música polifónica moderna. Si desplazamos la tónica a la nota D estaríamos tocando en el modo o escala D (a veces también conocido como clave D). Pero en ese caso el intervalo de una cuarta dejaría de ser una cuarta perfecta, ya que contendría dos tonos completos "pitagóricos", en lugar de un tono "pitagórico" y un tono cromático. Por lo tanto esta cuarta sonaría diferente. A menudo se critica la escala de Intervalos Justos debido a esta limitación: es inherentemente específica del modo. William Sethares responde a esta crítica como sigue [1, p.62]: "Muchos defensores de los Intervalos Justos (JI) no insisten en que toda la música se tenga que tocar necesariamente en JI. Simplemente si una pieza no encaja bien en el contexto de JI, no se debería tocar de esa forma. Además, los entusiastas de los Intervalos Justos típicamente están dispuestos a cambiar la afinación de sus instrumentos de una escala JI a otra para piezas específicas."
|
|
|
| Figura 27 |
6.2.- Comparación de intervalos entre escalas
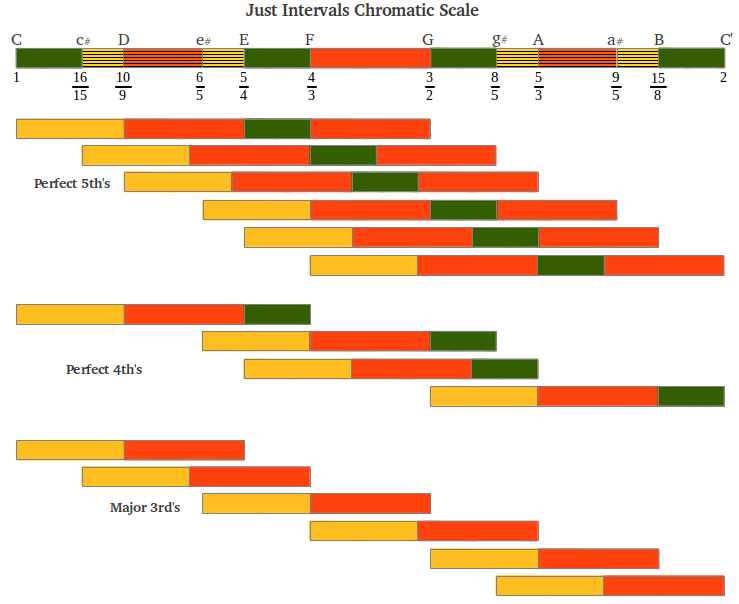
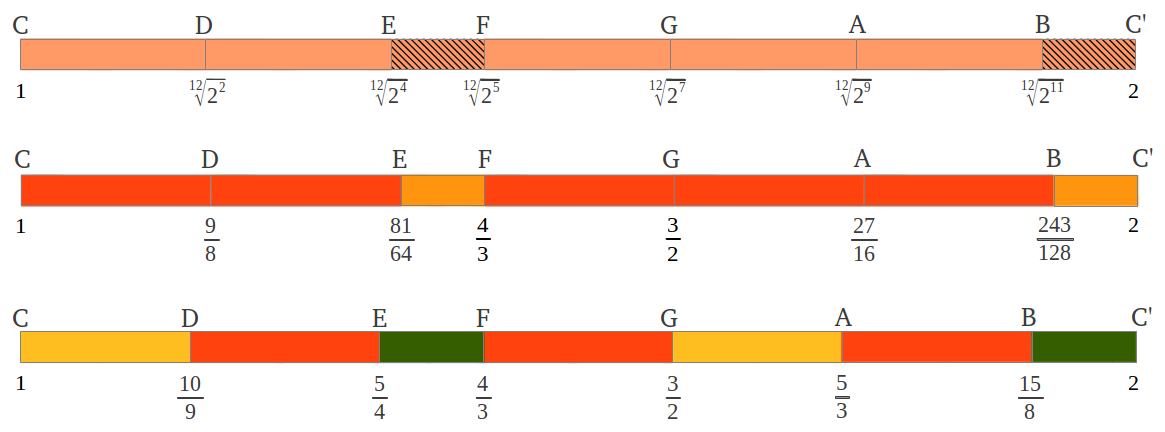
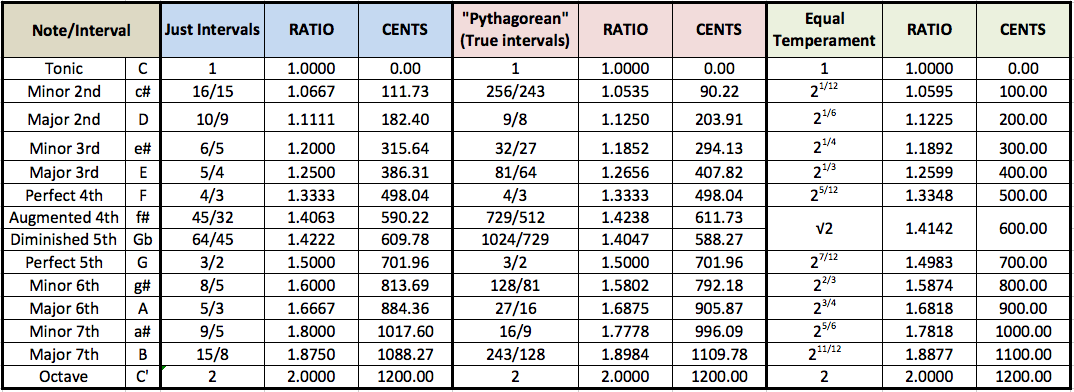
Existen algunas diferencias, tanto cuantitativas como cualitativas, en los intervalos de las escalas musicales discutidas hasta ahora. Las diferencias cuantitativas se resumen de forma gráfica en la Figura 28a para las escalas diatónicas y en la Figura 28b para las escalas cromáticas. Los valores correspondientes en cents se comparan en la Tabla 1. La escala "pitagórica" y la escala de los Intervalos Justos comparten la quarta y la quinta perfectas, mientras que las segundas, terceras, sextas y séptimas son marcadamente distintas. Resulta curioso darse cuenta de que los intervalos "pitagóricos" aparecen más cerca de los intervalos del Temperamento Igual que de los Intervalos Justos. En una sección posterior veremos cómo Maria Renold combinó lo mejor de estas dos escalas dando lugar a su Escala de las Doce Quintas. Lo que parece obvio es que las diferencias cuantitativas que existen entre los intervalos musicales, como es el caso de las diferencias claras entre los intervalos justos y los verdaderos, se deberían trasladar en diferencias cualitativas.
|
|
|
|
|
|
| Figura 28: Comparación gráfica de las escalas (a) diatónica y (b) cromática del Temperamento Igual, "pitagórica" y de Intervalos Justos. Las diferencias cuantitativas aparecen en la Tabla 1 de abajo. |
 |
|
| Tabla 1 |
Maria Renold ha dedicado muchos años de su vida al estudio y la comparación de las escalas musicales y sus intervalos, así como a una de sus cuestiones más profundamente sentidas como es la frecuencia de concierto correcta. Siguiendo su terminología, llamaremos intervalos verdaderos a los intervalos "pitagóricos" (Tabla 1). Con respecto a las diferencias cualitativas, ella ha constatado lo siguiente [2, p.15]: "Los intervalos que tienen distinta longitud y por tanto cualidades distintas son los más usados hoy en día para tocar música [...] Las diferencias cualitativas entre las terceras mayores justa y verdadera es que la primera suena pacífica, brillante y valiente, pero también se puede sentir que tiene una agudeza subyacente. En cambio la última pulsa un poco pero suena como si radiase luz. Entre las dos terceras menores puede experimentarse que la tercera manor justa suena no pulsante y triste, pero con una voluptuosidad subyacente; por el contrario, la tercera menor verdadera suena excitada. Entre las séptimas mayores se ha encontrado una diferencia destacable pero inesperada. Está comunmente aceptado que una séptima mayor justa 15:8 con 1088.27 cents tiene que resolverse hacia una consonancia cercana, ya sea para arriba o para abajo hacia la sexta mayor, si se quiere satisfacer al oido y liberar la increible tensión producida. Pero la séptima verdadera, apreciablemente mayor situada en 243:128 o 1109.78 cents, aunque obviamente tiene un carácter ligeramente disonante, suena brillante y pacífica, casi en suspensió, y no ejerce compulsión alguna sobre el oido humano que se deba resolver. Se puede disfrutar su brillantez y belleza con equanimidad y alegría, dejándola resonar sin resolver."
6.3.- Los intervalos justos en el monocorde
El monocorde es un "instrumento" sencillo supuestamente desarrollado por Pitágoras para estudiar las frecuencias y los intervalos musicales. Consiste en una cámara resonante, de una a tres cuerdas de piano, y en algunos casos una barra deslizante o puente móvil que permite seleccionar la porciónde la cuerda que se quiere tocar. Esto se muestra en la siguiente ilustración artesanal de Elsie Hamilton [5]:
 |
|
| Figure 29: Ilustración del monocorde por Elsie Hamilton. |
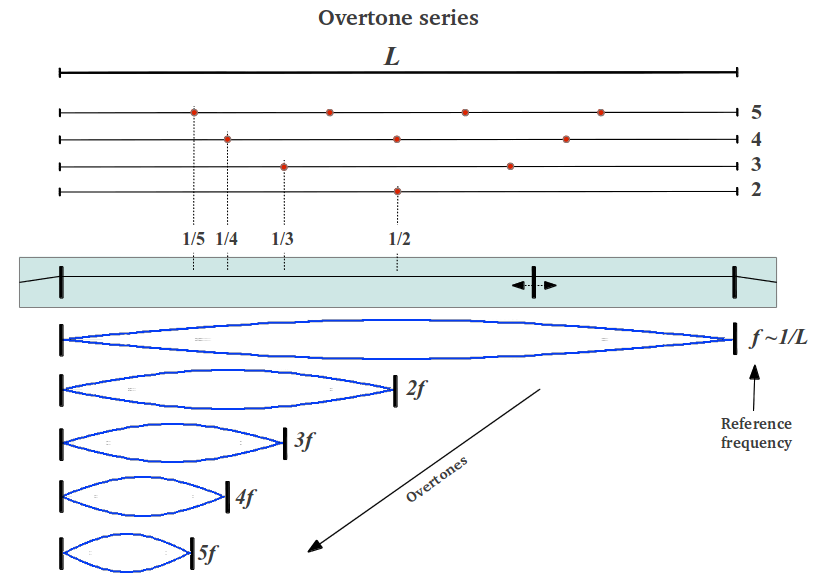
La cuerda tiene una frecuencia característica que está inversamente relacionada con su longitud. Cuando tocamos una cuerda de longitud L, se genera una onda estacionaria con una frecuencia fundamental proporcional a 1/L. Esta onda se propaga al medio colindante como una onda de presión longitudinal, y si su frecuencia cae en el rango audible (aproximadamente entre 20Hz y 20KHz) puede apreciarse con nuestros oidos. Si la cuerda se divide en dos mitades y se toca una de ellas -desplazando el puente móvil a la posición adecuada para mantener inmóvil el resto de la cuerda- se produce una frecuencia doble de la fundamental. Este proceso se puede iterar dividiendo la longitud de la cuerda en tres, cuatro y más partes para producir todos los múltiplos enteros de la frecuencia fundamental de la cuerda, también llamados armónicos o sobretonos (Figura 30).
 |
|
| Figura 30 |
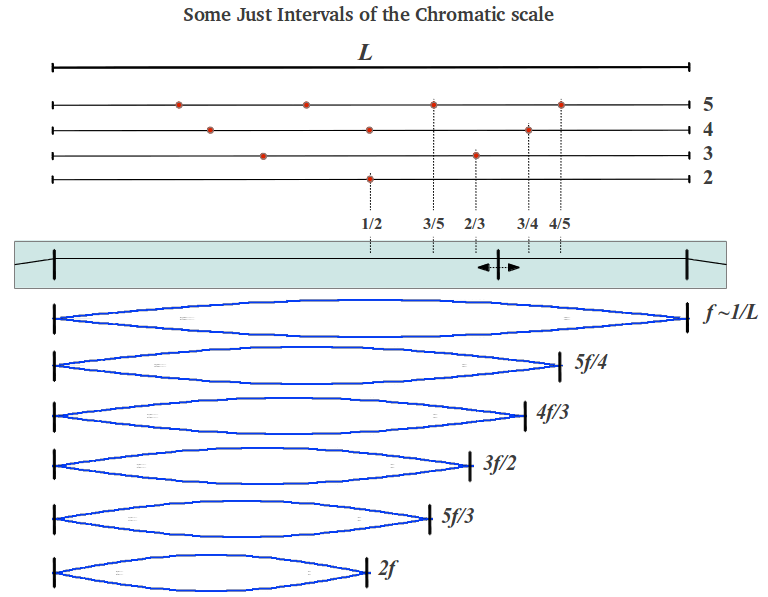
Este proceso puede generalizarse para producir frecuencias sonoras que estén relacionadas con la fundamental a través de cualquiera de los intervalos justos que hemos estudiado en esta sección (Figura 32): dividiendo la cuerda en tres partesy tocando 2/3 de su longitud produce una frecuencia 3/2 veces la fundamental, que es una quinta perfecta (tocando 1/3 de la longitud de la cuerda se produce una quinta perfecta pero situada una octava por encima). Dividiendo la cuerda en cuatro partes y tocando 3/4 partes produce una frecuencia que es la cuarta perfecta de la fundamental. De forma similar, una división de la cuerda en cinco partes permite generar la sexta mayor (3/5 partes) y la tercera mayor (4/5 partes). Estas marcas en el monocorde con una separación irregular son las mismas que podemos encontrar en una guitarra.
 |
|
| Figura 31 |
7.- Los Modos Aulós griegos
"Chicos, estudiad vuestros monocordes"
(Últimas palabras de Pitágoras)
7.1.-Antecedentes históricos
Cuando empecé a estudiar la estructura de las escalas musicales me sentí atraído por la simplicidad matemática del llamado método de "Afinamiento Ptagórico" que he explicado en la sección 2. Prácticamente en todas partes se atribuye esta escala a nuestro gran maestro griego Pitágoras, a pesar de que no existe ningún registro escrito que confirme este hecho. Como explica de forma clara Peter L.P. Simpson en su excelente revisión de los antiguos modos griegos [3], el registro escrito más antiguo sobre la música griega en el que la mayoría de estudiantes basan sus estudios se conoce como los Elementos Armónicos de Aristógeno, una colección de libros que han subrevivido prácticamente intactos. Estos libros contienen un ataque y una crítica a aquellos que Aristógeno llamaba los harmonistas de la escuela pitagórica, o en otras palabras los modalistas (porque harmonia designa modo musical en griego).
Aristógeno básicamente dice [3] que los modalistas no entendían lo básico acerca de la música y que lo hacían prácticamente todo mal. Para corregir sus errores y poner la ciencia de la música sobre suelo firme, Aristógeno tira por la borda toda la teoría que se llevaba en su tiempo y la reemplaza por algo nuevo. Desafortunadamente, en ese algo nuevo que él introduce no tienen cabida los modos tal y como se entendían de forma tradicional. Según Aristógeno, la forma de entender la música pasa por entender el canto, y la forma de entender el canto es empezar por el menor intervalo consonante, que es la cuarta perfecta. El siguiente intervalo consonante, la quinta perfecta, produce al juntarlo con la cuarta perfecta el último intervalo consonante que es la octava (según Aristógeno sólo existían esos tres intervalos consonantes). Todas la escalas de Aristógeno, incluyendo sus equivalentes de los modos antiguos -ya que utiliza el nombre de los modos para algunas de sus escalas- están constituidas por distintos tipos de tetracordes y sus combinaciones (ver sección 2).
La crítica principal a estos hechos históricos es la siguiente [3]: no existe ninguna razón para basar las escalas necesariamente en los tetracordes de Aristógeno, ni para construir los tetracordes de forma descendente -como Aristógeno siempre hacía- ni para limitar los intervalos consonantes a las cuartas, quintas y octavas. Aristógeno podía, y de hecho lo hizo, apelar a los límites impuestos por la capacidad de la voz humana, pero no existe razón alguna para construir la música, o su teoría, según esos límites. La música es mucho más rica en sus posibilidades de lo que Aristógeno permitió, pero él excluyó cuanquier otra posibilidad desus enseñanzas, probablemente porque en realidad no entendía lo que los pitagóricos estaban en realidad haciendo.
El hecho es que existen otras escalas Justas aparte de las que hemos discutido hasta ahora. Citando a Maria Renold [2,p.27]: "Aunque raramente utilizadas en la música occidental durante los últimos cuatrocientos o quinientos años, se conocen desde tiempos antiguos y se han venido utilizando hasta el momento entre las gentes de Asia, Grecia, las islas de Escocia, América del Norte, etc. Estas escalas, que aquí llamamos los siete Modos Aulósde la antigua Grecia, se llaman 'harmonai' por su redescubridora la musicologista [y Fellow del Instituto de Arqueología de la Universidad de Liverpool] Kathleen Schlesinger. Cmo cuidadora de instrumentos musicales antiguosen el Museo Británico, ella se dió cuenta de que los agujeros para los dedos de los aulós griegos parecían ser equidistantes. Gracias a su entrenamiento específico supo que esos instrumentos no podían producir las escalas y los intervalos de hoy en día. Por lo tanto esas escalas tenían que ser distintas. Schlesinger estableció los tipos y la forma de esas escalas durante más de 25 años de investigación publicados en 1938 en su libro Los Aulós Griegos". Según Elsie Hamilton, una de sus discípulas, "la Sra. Schlesinger era de la opinión que los Modos nacieron mucho antes incluso de la época de Pitágoras [...] ella apunta a que podemos remontarnos hasta alrededor del año 2800 B.C. a las flautas de plata de Ur en Caldea, que fueron excavadas bajo la dirección de Sir Leonard Woolley, y en las cuales encontramos orificios a distancias iguales y que, estando hechas de plata, han resistido el paso del tiempo [5]."
7.2.- Una forma alternativa de estudiar el monocorde
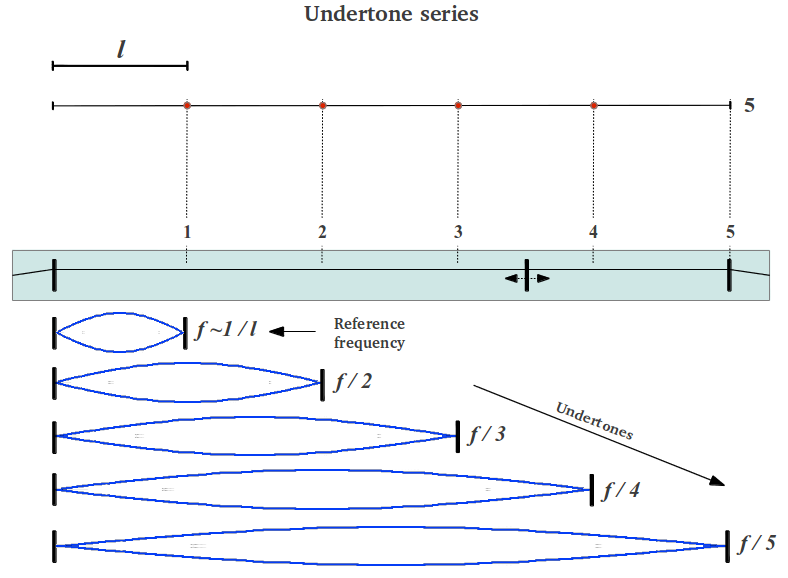
Hay una forma más simple de estudiar las frecuencias sonoras usando el monocorde que dividir su cuerda en un número desigual de partes cada vez. ¿Y si lo dividimos en un número fijo de partes a ver qué sucede? En la Figura 32 mostramos un ejemplo del monocorde dividido en cinco segmentos iguales. La cuerda entera proporciona una frecuencia de referencia que habitualmente es la tónica en la teoría musical moderna, y a partir de la cual se forman todos los intervalos restantes en orden ascendente (ver Figura 31). Sin embargo, el segmento más pequeño en la cuerda así dividida proporciona otra frecuencia de referencia, en realidad la frecuencia más alta para un número de segmentos dado. Tocando un número creciente de segmentos cada vez genera el sonido de fracciones más y más pequeñas de esa frecuencia más alta, que se conocen como subtonos (Figura 32).
 |
|
| Figura 32 |
A través de este sencillo ejemplo podemos empezar a aprecir las posibilidades ilimitadas de esos subtonos. El primer subtono (f/2) forma con la frecuencia (más alta) de referencia f el intervalo de una octava, aunque en dirección descendente. Tomando tres segmentos obtenemos el siguiente subtono, que forma un intervalo de una quinta perfecta descendente con el segundo subtono ya que (f/3)/(f/2) = 2/3. A continuación encontramos otra octava en f/4. El cuarto subtono f/5 nos permite estudiar el intervalo de una sexta (5/3) con el segundo subtono, y también el de una tercera mayor (5/4). La octava siguiente no se encuentra hasta la frecuencia f/8, por lo tanto las sucesivas octavas descendentes contienen un número creciente de intervalos (densamente empaquetados).
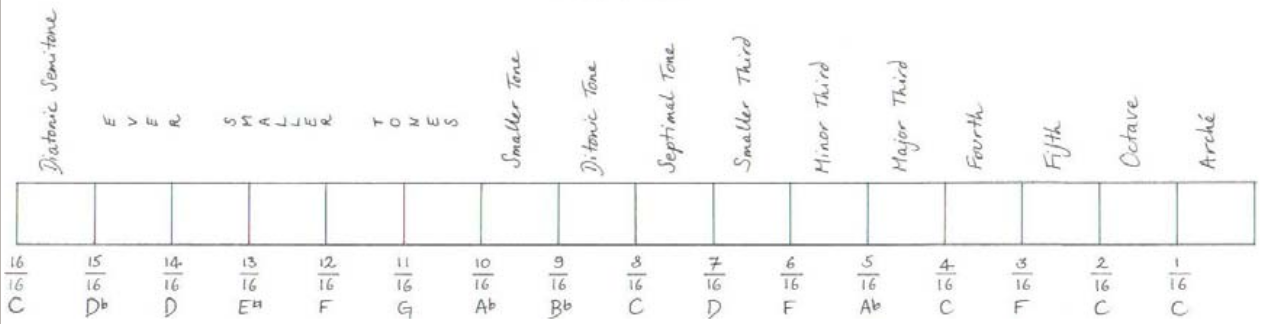
El diagrama siguiente de Elsie Hamilton ilustra este hecho hasta los 16 segmentos. Por favor obsérvese lo siguiente: (1) la longitud de cada segmento no es proporcional al intervalo correspondiente como en nuestros dibujos de colores; (2) las fracciones que se muestran corresponden a divisiones de la longitud de la cuerda -not a frecuencias; y (3) el número de segmento aumenta de derecha a izquierda. A partir de este diagrama resulta interesante apreciar que las primeras tres octavas (hasta el octavo subtono) contienen la mayoría de intervalos de la escala Justa, como se ha explicado en la Figura 32 de arriba en dirección opuesta. Para ser capaz de tocar cualquiera de esos intervalos, necesitaríamos un monocorde con almenos dos cuerdas. Si ese fuera el caso, manteniendo una cuerda por ejemplo en el quinto segmento y la otra cuerda en el tercer segmento produciría el sonido de una sexta mayor descendente (3/5).
 |
|
| Figure 33: División de un monocorde en 16 segmentos iguales ilustrada por Elsie Hamilton [5]. Los números que se muestran son fracciones de la longitud de la cuerda, la frecuencias correspondentes serían sus valores inversos. Tocando un número creciente de segmentos proporciona una secuencia de subtonos 16/2, 16/3, 16/4, ... de la frecuencia de referencia mayor 16/1 también conocida como arché, hasta alcanzar la frecuencia menor 16/16 al usar la cuerda entera. |
Los Modos Aulós antiguos empiezan en la siguiente octava, la que se encuentra entre los subtonos 8º y 16º. Siguiendo el método de Maria Renold's, voy a mostrar como se puede deducir de forma sencilla el primero de esos modos usando exclusivamente la media armónica.
7.3- Deducción a partir de la media armónica
Seleccionemos la octava contenida entre las frecuencias del 16º subtono (f/16) y el octavo (f/8) de la frecuencia de referencia f o Arché que no debe confundirse con la tónica de la escala que en nuestro caso sería f/16. Como ya hemos visto en la Figura 24, la media armónica de la octava genera la cuarta nota (en realidad una cuarta perfecta). Ahora si continuamos com media armónicas en lugar de cambiar a la media aritmética, obtenemos la frecuencia de las seis notas restantes tal como sigue::
|
(a) |
|
|
(b) |
|
|
(c) |
|
|
(d) |
|
|
(e) |
|
|
(f) |
|
|
(g) |
|
 |
|
| Figura 34: La estructura de las escalas en los antiguos Modos Aulós griegos puede obtenerse a partir de la media armónica. |
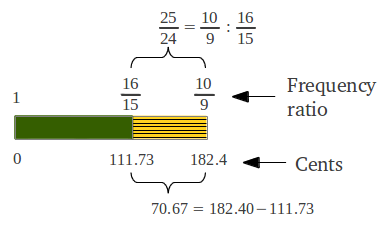
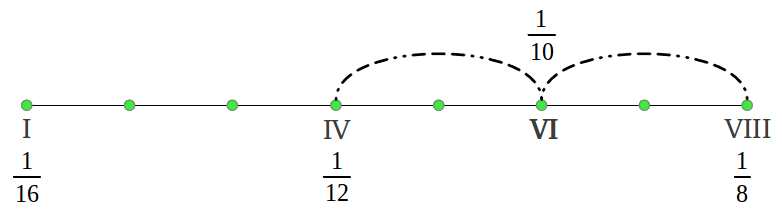
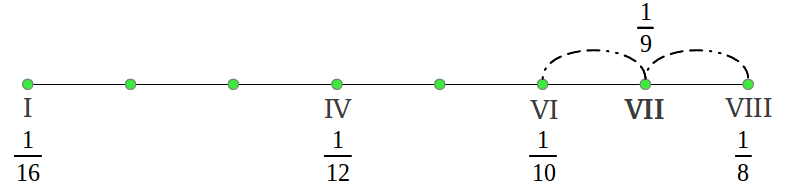
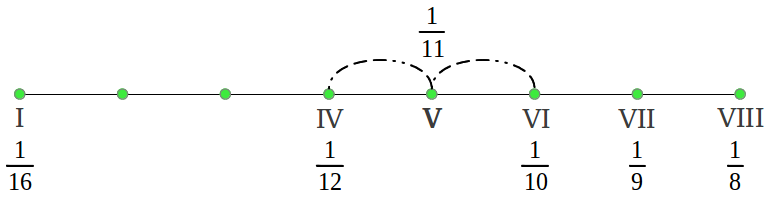
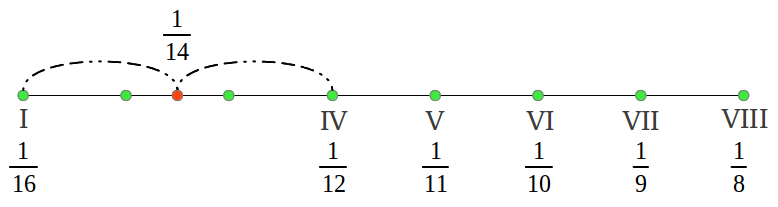
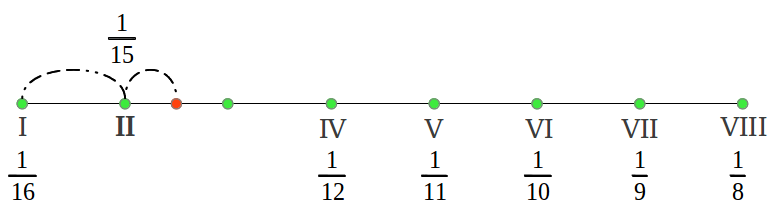
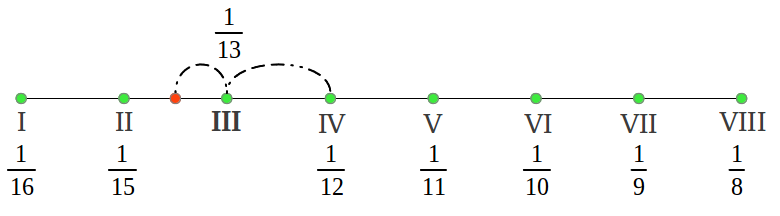
Lo que hemos obtenido es lo que los matemáticos llaman una serie armónica, excepto por la fracción ausente 1/14 que sería una novena nota en la escala. Esas son las frecuencias del antiguo Modo Hipodorio de Saturno [2]. Las notas en los Modos Aulós a menudo se numeran en términos del número de segmento que produce cada nota that produces each note [2]. La Figura 35 muestra las longitudes de intervalos reales en cents siguiendo esa numeració u utilizando nuestra convención de colores (véase la leyenda de colores en la Figura 38 más adelante). podemos observar que el primer intervalo es (1/15)/(1/16) = 16/15 o un semitono cromático, los siguientes cuatro intervalos 15/13, 13/12, 12/11 and 11/10 son "nuevos" para nosotros y son característicos de los Modos griegos, y los últimos dos intervalos también nos suenan familiares: 10/9 el tono justo y 9/8 el tono "pitagórico".
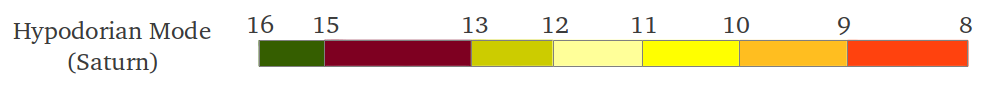 |
|
| Figure 35 |
Para tocar esta escala en un monocorde, tendríamos que dividirlo en 16 segmentos iguales como en la Figura 33 anterior y utilizar sólo la segunda mitad de las divisiones. Por favor obsérvese que, a pesar de estar basados en la serie de subtonos, cuando se lee de izquiera a derecha el Modo Hipodorio de Saturno en realidad es una escala ascendente.
7.4.- Los siete antiguos Modos griegos
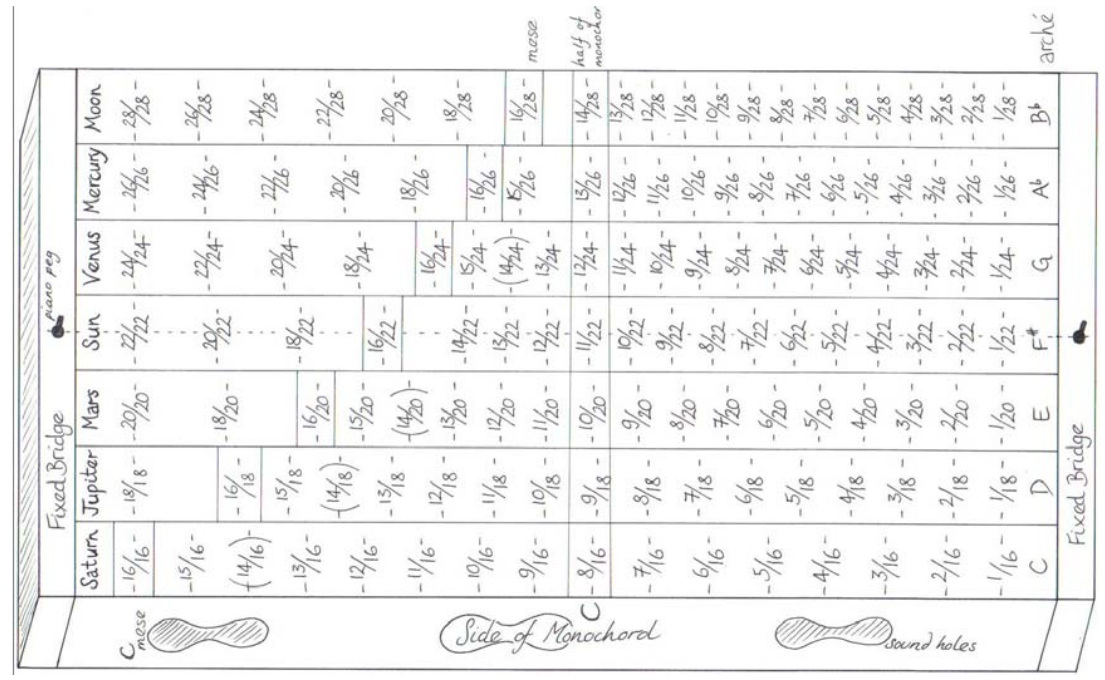
Los seis Modos griegos restantes se obtienen usando 18, 20, 22, 24 y 28 divisiones de la cuerda, como se ilustra en el siguiente diagrama original de Elsie Hamilton [5]:
 |
|
| Figura 36: Divisiones en un monocorde para tocar los siete Modos Aulós griegos. |
Podemos observar en este diagrama que cada modo tiene un segmento básico de longitud distinta, ya que que la longitud total de la cuerda es la misma. Así pues, la frecuencia de referencia o Arché es diferente para cada modo. Por ejemplo si ajustamos la longitud total de la cuerda L de manera que su fundamental sea f0 ~1/L = 128Hz, entonces el Arché del modo de Saturno sería f=128/(1/16) = 128·16 = 2048 Hz, pero el modo del Sol tendría una Arché f = 128·22 = 2816 Hz. Por favor obsérvese que las notas que se encuentran por debajo (a la izquierda) del 16º subtono usan los subtonos dobles de la octava diatónica (8º a 16º) omitiendo los subtonos que se encuentran enmedio: por ejemplo los cuatro subtonos más bajos del modo del Sol son 1/22, 1/20, 1/18, 1/16. El diagrama de arriba puede malinterpretarse porque el primer segmento, el que se encuentra entre la primera división y el inicio de la cuerda, parece tener la misma longitud en cada modo y eso no es así como acabamos de explicar.
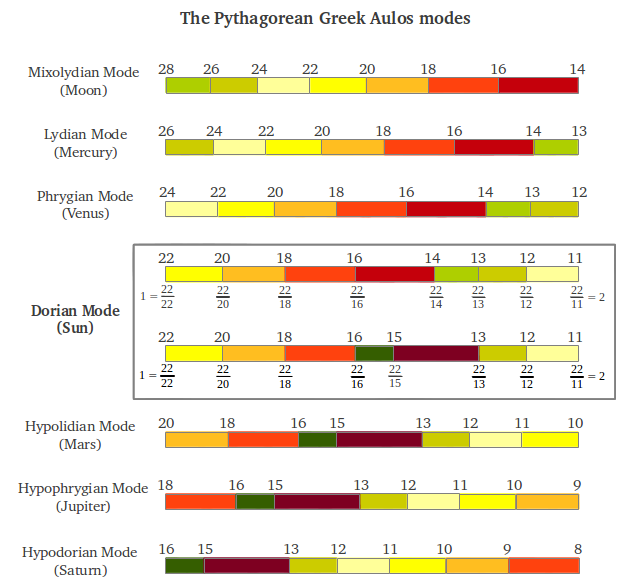
Ahora viene la parte interesante. ¿Cuál es la estructura de intervalos de los seis nuevos modos que acabamos de obtener? Si se realizan los cálculos matemáticos, uno termina dándose cuenta de que todos los modos contienen los mismos intervalos pero en un orden diferente. Esto se ilustra de forma gráfica en la Figura 37. El modo central Dorio asociado al Sol era el modo principal en el antiguo sistema musical griego. Nótese que este modo tiene dos formas, una usando la división 1/14 y la otra usando la división 1/15; no todos los modos tienen esas dos formas (véase la Figura 40) pero esas dos divisiones nunca se usaban simultáneamente en ningún modo.
 |
|
| Figura 37 |
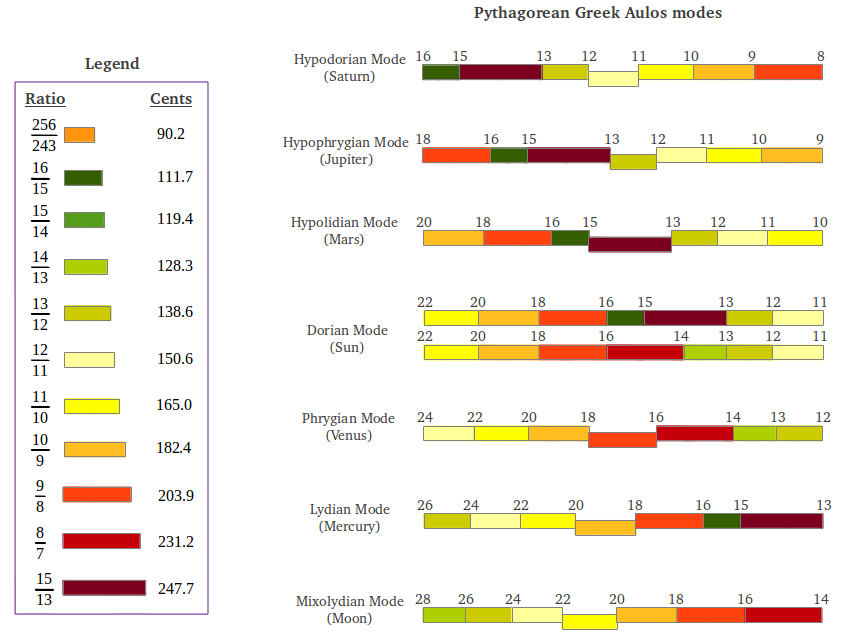
Los siete antiguos Modos griegos tienen una particularidad característica: cada uno está formado por dos tetracordes distintos. Esto se ilustra en la figura siguiente, donde se muestra la laongitud de cada intervalo en cents. Se puede apreciar que cada modo puede generarse a partir del modo precedente cogiendo el último intervalo e insertándolo al principio, realizando un desplazamiento cíclico (excepto en los casos en queel intervalo 15/13 se reemplaza por el intervalo 15/14 o al revés, Figura 38).
 |
|
| Figure 38: Los antiguos Modos Auló griegos como tetracordes. |
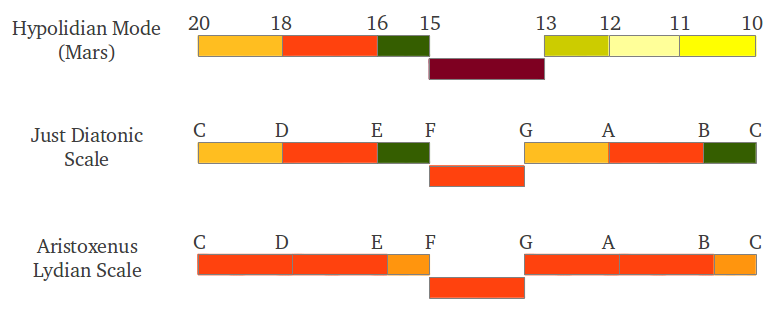
¿Alguno de los anteriores tetracordes le resulta familiar? Como probablemente habrá adivinado, se trata del primer tetracorde del Modo Hipolidio de Marte. La escala moderna de Intervalos Justos utiliza este tetracorde en realidad dos veces, siguiendo la disposición típica propuesta por Aristógeno (Figura 39). Parece que la escala diatónica moderna ha perdido la pureza o diversidad de intervalos original que solía tener en el antiguo Modo Hipolidio.
 |
|
| Figura 39: Nuestros escala moderna de Intervalos Justos contiene el primer tetracorde del Modo Hipolidio asociado a Marte. |
7.5.- Los Modos Aulós griegos como subespecies
Para poder tocar los siete modos distintos en un sólo instrumento, éste se debería reafinar cada vez porque el número de divisiones de la cuerda es distinto en cada modo. Sin embargo, existe una forma de superar esta limitación aparente. El truco consiste en dividir la cuerda en un número de segmentos suficientemente grande (al menos 28), y en "acomodar" cada modo en una porción distinta de la cuerda. Con esta operación, los siete modos comparten el mismo intervalo medio 18/16 (que los antiguos griegos llamaban mese) y también tienen la misma frecuencia de referencia, pero cada modo tiene su propia tónica y, por sorprendente que pueda parecer a primera vista, ¡su estructura de intervalos no se ve alterada! La figura siguiente lo ilustra de forma gráfica, reproduciendo la Tabla 5 del libro de Maria Renold [2, p.30].
 |
|
| Figure 40: Los antiguos Modos griegos como especies. |
Según Elsie Hamilton, quien ha adoptado los Modos griegos como base para sus composiciones musicales, "con los siete Modos Planetarios no sólo tenemos dos experiencias distintas como en nuestras escalas modernas Mayor y Menor, sino almenos siete, porque cada uno de los Modos griegos nos proporciona un "ethos" o atmósfera completamente diferente, que resulta bastante individual y peculiar de ese modo en concreto; de esta forma nuestra experiencia musical se ve enormemente enriquecida". Otra ventaja es que "el Modo griego está construido siguiendo la propia Ley Natural (la Serie Armónica) sin ningún compromiso [como sucedía en la espiral de quintas de la escala de Aristógeno], y a un afinador de pianos le resulta mucho más fácil afinar un piano a los Modos que afinarlo según el método ordinario, con sus complicaciones de pulsos y demás" [5].
8.- La escala de Doce Quintas
8.1.- La estructura de la escala y las quintas formadas
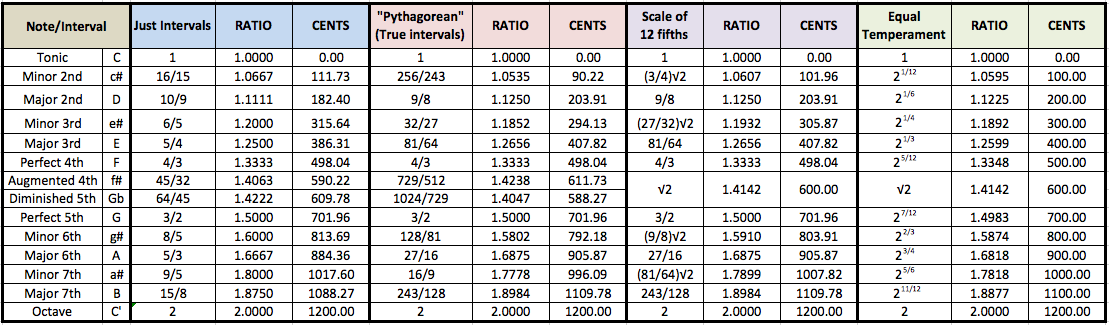
En 1962, partiendo de la escala C "pitagórica" que hemos presentado en la sección 2, Maria Renold encontró de oído una escala cromática de doce tonos en la cual todas la claves mayores y menores son posibles, y que está hecha por completo de lo que ella llama intervalos genuinos para el oido. A esta escala la llamó la escala de las Doce Quintas [2]. La estructura de la escala es muy simple: empezando por las siete notas de la escala C "pitagórica", se inserta un nuevo tono enmedio de cada tono completo que surge de la media geométrica de las dos frecuencias extremas del tono completo en cuestión (Figura 41). Esto es equivalente a situar los cinco semitonos extra -que corresponden a las teclas negras del piano- en el centro exacto del tono completo expresado en cents. La figura siguiente muestra los cocientes de intervalos acumulados de la escala de doce notas obtenida siguiendo este método. En la Tabla 2 se compara la longitud de los intervalos resultantes en cents con los de las escalas cromáticas vistas hasta el momento. Para que quede claro que los cinco nuevos tonos son medias geométricas y para diferenciarlos de los tonos ordinarios y de los tonos del tempramento igual, Se los llamó Delis, Elis, Gelis, Alis and Belis -en alemán Ges significa llano y Gis significa agudo, luego Gelis contiene ambos nombres indicando así que esos semitonos no son ni llanos ni agudos [2, p.8].
 |
|
| Figura 41 |
 |
|
| Table 2 |
Es importante enfatizar que los cinco tonos que son medias geométricas se encontraron de oido. Las cualidades de estos nuevos intervalos difieren de los intervalos de las escalas Justa y de Aristógeno, por lo que Maria Renold los llamó intervalos "formados". Según ella, "estos intervalos formados se armonizan con los intervalos verdaderos consiguiendo armonías bien sonantes y disonancias características". Los doce tonos forman "una escala cromática con un sonido genuino y 24 escalas mayores y menores con un sonido igualmente genuino que son válidas pra realizar cualquier trabajo de composición con instrumentos de afinamiento fijo. Una prueba con cualquier instrumento afinado de esta forma demuestra que este este es el caso, convirtiendo en innecesario afinamiento del Temperamento Igual, con un sonido tan falso e insatisfactorio" [2, p.57].
Los pianos se pueden afinar a la escala de doce quintas. El público comentaba que el sonido del piano de Maria Renold con la nueva afinación no parecía proceder directamente del propio instrumento "sino que sonaba libremente como si procediera del centro de la habitación. Un tono de sonido libre similar se observó en un coro de unas 20 liras afinadas de esta forma; músicos y público experimentaron una plenitud de sonido inspirante que provenía del medio de la habitación [...] Parece que con anterioridad sólo eran capaces de crear este tono en la composición activa de música los artistas, instrumentistas y directores que tenían un don especial. La escala de doce quintas parece ser capaz de hacer aparecer este tono a través tan sólo de las proporciones de intervalos entre tonos" [2, p.63].
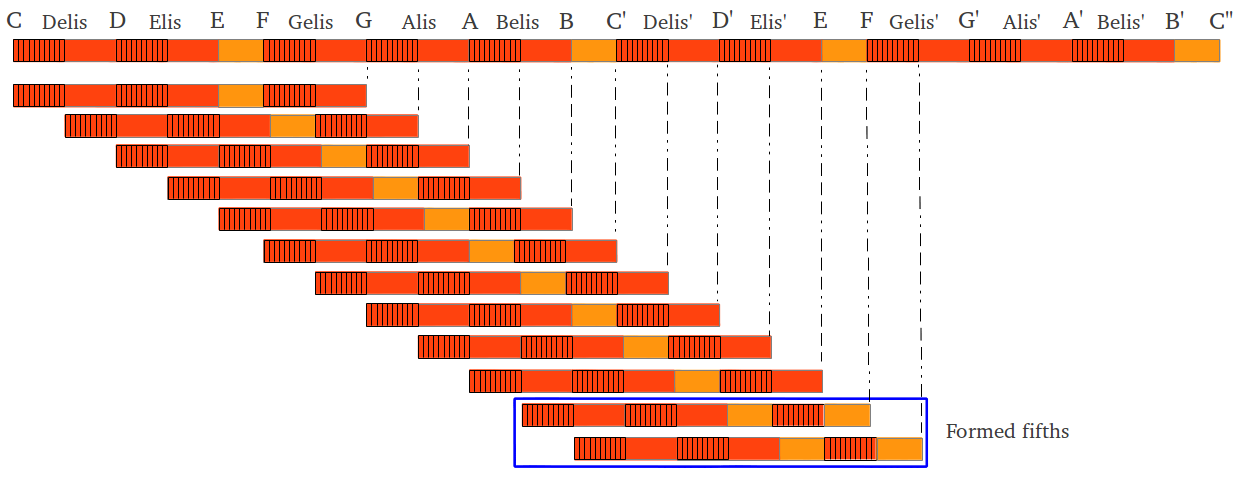
Maria Renold destaca que su escala de doce quintas "sólo fue posible después de descubrir lo que llama la quinta formada. El hecho de que existe una quinta genuina para el oido que es menor que la quinta del Temperamento Igual es un fenómeno que sólo se puede descubrir de oído. La quinta formada se puede reconocer por su carácter ligeramente crudo o seco. Difiere de todas las otras quintas que han sido clasificadas de forma acústica hasta el momento presente" [2, p.61]. La figura siguiente ilustra las doce quintas de esta escala; diez de ellas son quintas perfectas y dos de ellas son quintas formadas -que contienen dos semitonos "pitagóricos"en lugar de uno solo:
 |
|
| Figura 42: The fifths in Maria Renold's scale of twelve fifths. |
8.2.- Acerca de la frecuencia de afinación correcta A=432Hz
Maria Renold pone de manifiesto que "conviene tener presente una característica clave de la escala de doce quintas. Mientras que los intervalos y tonos tienen efecto bonito, placentero y armónico sobre el ser humano cuando se afinan a C=256Hz, Gelis=362.04Hz y A=432Hz, se convierten en antisociales y además causan que las personas se provoquen las unas a las otras si se utiliza la frecuencia de afinación A=440Hz [de uso común hoy en día]. Esta observación hecha a menudo muestra que los intervalos genuinos al oído no son lo único que importa en música, sino que tonos de determinadas frecuencias tienen determinadas cualidades que pueden tener efectos mayores sobre los seres humanos" [2, p.63]. Este comentario surgió a partir de las experiencias siguientes:
"La primera vez que Maria Renold (violista y violinista de concierto) afinó su gran piano Steinway al recién hallado método de afinación, el único diapasón de que disponía era a A=440Hz, por lo que el piano se afinó según esta frecuencia. Una vez hecho, fue una ocasión para celebrar y se tocó música de inmediato con ese instrumento y su sonido absolutamente magnífico. Piezas tanto clásicas como modernas sonaban con una belleza nunca antes oída, pero después de unos momentos de desarrolló una atmósfera crecientemente maliciosa entre los presentes".
"Parecía totalmente improbable que los intervalos de ese nuevo método, que sonaban perfectamente claros y armónicos, pudieran levantar un estado de ánimo tan antisocial entre los oyentes. Sin embargo, así era. La solución sólo se encontró cuando se reafinó el piano a la frecuencia C=256Hz sugerida por Rudolf Steiner, la llamada 'C del filósofo'. Cuando se tocó más música en el piano nuevamente afinado, entonces sí fue una verdadera celebración. El malestar experimentado anteriormente había desaparecido y tanto los intervalos como los tonos sonaban placenteros y bellos. Todos los presentes se deleitaron con el espléndido sonido y se vieron envueltos por un estado de ánimo armónico que dejaba a la gente libre".
"Para asegurarse de la primera observación, musicalmente inusual, no se trataba de un error, se repitió el experimento con liras durante muchos años y en muchos lugares. El mismo fenómeno siempre tenía lugar. Esa observación sólo puede conducir a una conclusión: sólo pueden ser los tonos basados en la frecuencia de afinación A=440Hz los que causan ese estado de ánimo antisocial" [2, p.69].
Entonces surge de forma natural la pregunta ¿es esa observación también válida para las demás escalas como el ámpliamente extendido Temperamento Igual? En el siguiente artículo describiremos los experimentos llevados a cabo por Maria Renold para confirmar que en efecto así es.
9.- Referencias
[1] Sethares, William A: "Tuning, Timbre, Spectrum, Scale", Springer, 2004.
[2] Renold, Maria: "Intervals, Scales, Tones and the Concert Pitch c = 128 Hz", Temple Lodge, 2004.
[3] Simpson, Peter LP: "The sound of Music: On the Ancient Greek Modes".
[4] Kappraff, Jay: "Beyond Measure, A Guided Tour Through Nature, Myth, and Number", World Scientific, 2002.
[5] Hamilton, Elsie: "The Modes of Ancient Greece", 1953.