Sólidos Arquimedianos

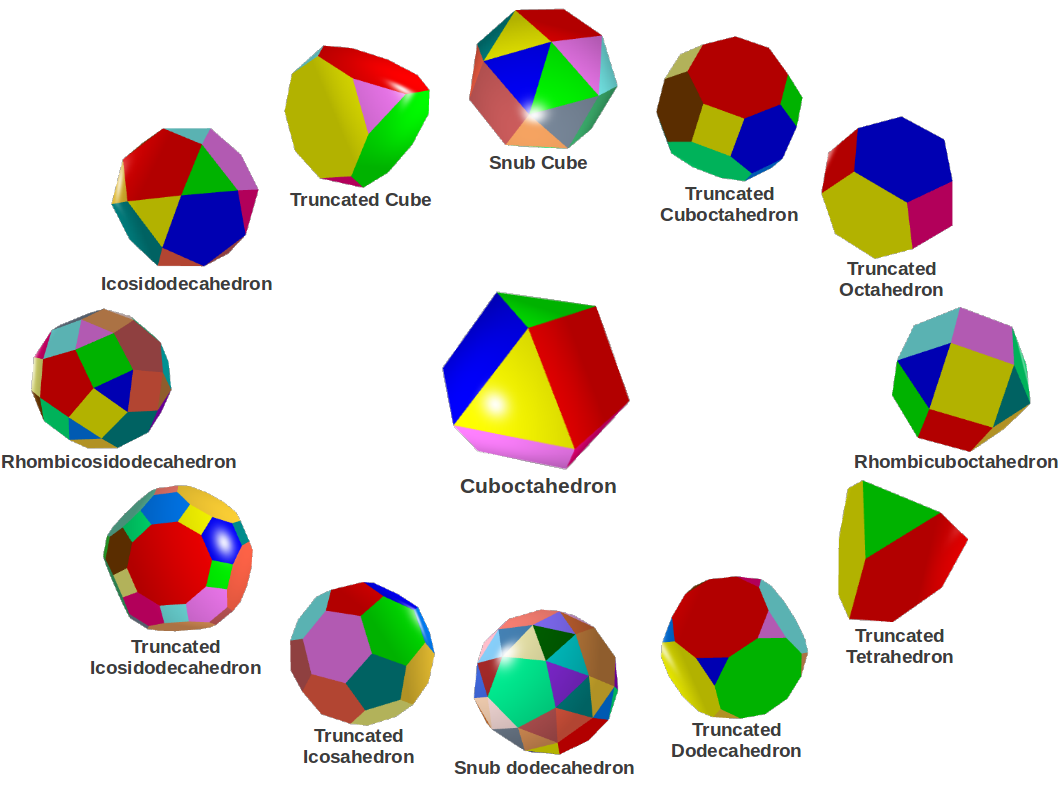
Los Sólidos Arquimedianos son los únicos 13 poliedros convexos, con vértices idénticos y cuyas caras son polígonos regulares (aunque no iguales como en los Sólidos Platónicos). Como todos los vértices son iguales entre ellos, estos sólidos se pueden describir indicando qué polígonos regulares se unen en cada vértice y en qué orden. Por ejemplo el Cuboctaedro tiene dos triángulos y dos cuadrados que se unen en cada vértice de forma alternada, así que se denota (3,4,3,4).

Cinco de los Sólidos Arquimedianos se derivan de los Sólidos Platónicos por un proceso de truncado (cortar las equinas) con un porcentaje inferior a 1/2. El porcentaje de truncado f varía en cada sólido; el objetivo es obtener nuevos polígonos regulares como caras. Su fórmula general es

$$f=\frac{1}{2+\alpha }$$

donde el factor α depende de la forma de la cara original: un triángulo (Tetraedro,Octaedro e Icosaedro), un cuadrado (Cubo), o un pentágono (Dodecaedro) y viene dado por:

$$\alpha =\{\begin{array}{c}1\mathrm{Triángulo}\\ \sqrt{2}\mathrm{Cuadrado}\\ \phi \mathrm{Pentágono}\end{array}$$

La imágenes siguientes ilustran estos cinco primeros Sólidos. Al hacer click en cualquiera de ellas se obtiene un modelo 3D del sólido que se puede ampliar y rotar a voluntad:

Tetraedro Truncado (3,6,6) $$f=\frac{1}{3}$$	Cubo Truncado (3,8,8) $$f=\frac{1}{2+\sqrt{2}}$$	Octaedro Truncado (3,8,8) $$f=\frac{1}{3}$$	Icosaedro Truncado (5,6,6) $$f=\frac{1}{3}$$	Dodecaedro Truncado (3,10,10) $$f=\frac{1}{2+\phi }$$

Hay otros dos Sólidos Arquimedianos especiales que pueden obtenerse truncando por completo (f=1/2) dos Sólidos Platónicos duales cada uno de ellos: el Cuboctaedro, que proviene de truncar o bien el Cubo o su dual el Octaedro. Y el Icosidodecaedro, que proviene de truncar el Icosaedro o su dual el Dodecaedro. De aquí su "doble nombre":

Cuboctaedro		Icosidodecaedro

Los próximos dos sólidos, el Rombicuboctaedro y el Rombicosidodecaedro, aparentemente parecen provenir de truncar los dos sólidos precedentes. Sin embargo, resulta parente de la discusión anterior sobre el porcentaje de truncado f que uno no puede truncar un sólido con caras de distinta forma y terminar con polígonos regulares como caras.

Por lo tanto, estso dos sólidos deben construirse con otra técnica. En realidad se pueden construir a partir de los Sólidos Platónicos originales mediante un proceso conocido como expansión. Este consiste en separar progresivamente las caras del poliedro original con simetría esférica, hasta un punto en que se puedan unir mediante nuevas caras que sean polígonos regulares. Este proceso se ilustra en la figura siguiente:

Rombicuboctaedro		Proceso de expansión     (de Wikipedia)

 

Rombicosidodecaedro		Proceso de expansión     (de Wikipedia)

El nombre de Cuboctaedro Truncado (también llamado Gran Rombicuboctaedro) y el de Icosidodecaedro Truncado (también conocido como Gran Rombicosidodecaedro) parecen indicar que estos sólidos se derivan de truncar el Cuboctaedro y el Icosidodecaedro. Pero tal como acabamos de razonar esto no es posible.

Cuboctaedro Truncado		Icosidodecaedro Truncado

Por último, existen otros dos sólidos especiales que tienen dos formas o variaciones quirales (simetría especular): el Cubo romo y el Dodecaedro romo. Aquí mostramos sólo una de las formas quirales de cada uno de ellos:

Cubo romo		Dodecaedro romo

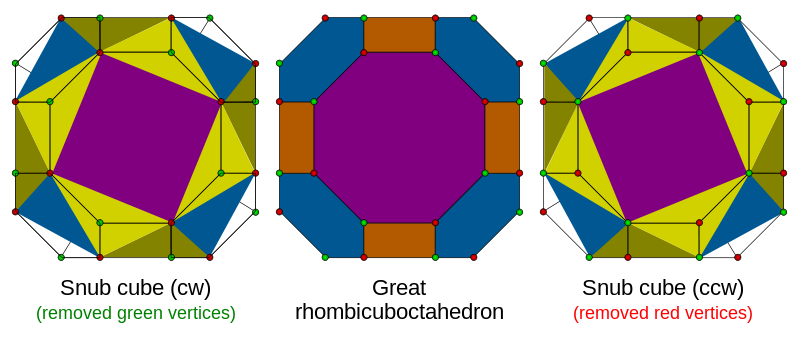
Estos sólidos pueden construirse por alternancia de otro Sólido Arquimediano. Este proceso consiste en eliminar vértices alternos y crear nuevos triángulos en los vértices eliminados. La figura siguiente ilustra este proceso para el caso del Cubo romo, que parte del Cuboctaedro Truncado (también llamado Gran Rombicuboctaedro):

Puedes encotrar una tabla resumen de los Sólidos Arquimedianos en el artículo dedicado a sus duales los Sólidos de Catalan.