- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Phi en los Sólidos Sagrados
1.- Introducción
Los Sólidos Platónicos pueden clasificarse en dos grupos: los que no tienen la Proporción Aurea en su constitución (el tetraedro, el cubo y el octaedro) aquellos que sí que involucran la Proporción Aurea, que son el Dodecaedro y el Icosaedro. Estos dos grupos son invariantes bajo la operación de calcular el dual, es decir los duales de todos estos sólidos permanecen en el mismo grupo. Algo parecido suced con los Sólidos Arquimedianos y sus duales los Sólidos de Catalan: por ejemplo en cuboctaedro y su dual, el dodecaedro rómbico, ambos pertenecen al primer grupo (los no relacionados con la Proporción Aurea).
En cualquier artículo sobre el Cubo de Metatrón se encuetra la afirmación de que esta estructura contiene todos los Sólidos Platónicos en su interior. En mi artículo sobre el Cubo de Metatrón he mostrado que esto no es verdad: la red interna del cubo es una teselación del espacio compuesta de tetraedros y octaedros alternados. Los sólidos que pueden hallarse en el Cubo de Metatrón no involucran la Proporción Aurea: la red interna del cubo genera el tetraedro, el octaedro, el octaedro estrellado y el cuboctaedro, pero no genera ni el icosaedro ni el dodecaedro. Este hecho puede suscitar una pregunta colateral: ¿forman estos sólidos relacionados con la Proporción Aurea alguna red? Tal vez. Lo que mostraré es que la interconexión interna de sus vértices y la prolongación externa de sus aristasconducen a una serie de Estelaciones interconectadas como el que se conoce como Doble Pentadodecaedro.
No he sido capaz de encontrar ningún poliedro convexo que contenga los cinco Sólidos Platónicos, es decir, cuyos vértices en coordenadas cartesianas permitan la construcción de todos ellos. La mejor aproximación a esta tarea es el Triacontaedro Rómbico: mostraré que sus vértices definen todos los Sólidos Platónicos excepto el octaedro. Si uno quiere incluir los vértices de octaedro, ellos lo lleva a un sorporendente poliedro non convexo que realmente contiene todos los Sólidos Platónicos, y mucho más: se lo conoce como el Poliedro 120, y ha sido extensamente estudiado por Robert W. Ray.
2.- La Proporción Aurea en los Sólidos Platónicos
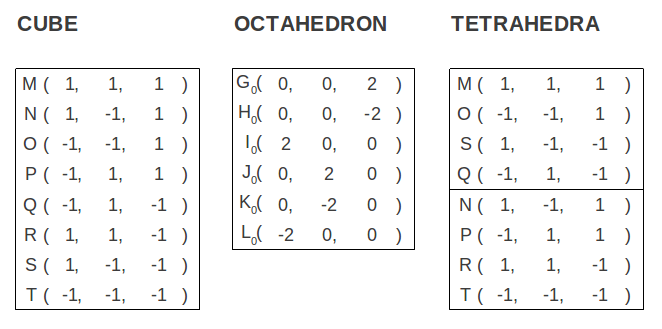
Es bien sabido que el poliedro regular más simple, el tetraedro, está contenido en el interior del cubo. Por lo tanto puede construirse con la mitad de los vértices de un cubo (Figure 1). El dual de este último es el octaedro, luego sus vértices son los puntos medios de las caras del cubo. Todos estos sólidos tienen en común el hecho de que sus coordenadas cartesianas no involucran la Proporción Aurea. De hecho, todos ellos quedan definidos por puntos del espacio con coordenadas enteras (ver Figura 1 y Tabla 1).
 |
 |
 |
 |
| (a) | (b) | (c) | (d) |
| Figura 1: El octaedro, el cubo y los dos tetraedros contenidos en este último, que definen una estrella tetraedro o tetraedro estrellado. | |||
 |
||
| Tabla 1: Los vértices del cubo, octaedro y tetraedro mostrados en la Figura 1, en coordenadas cartesianas. Todos ellos pueden representarse mediante números enteros. |
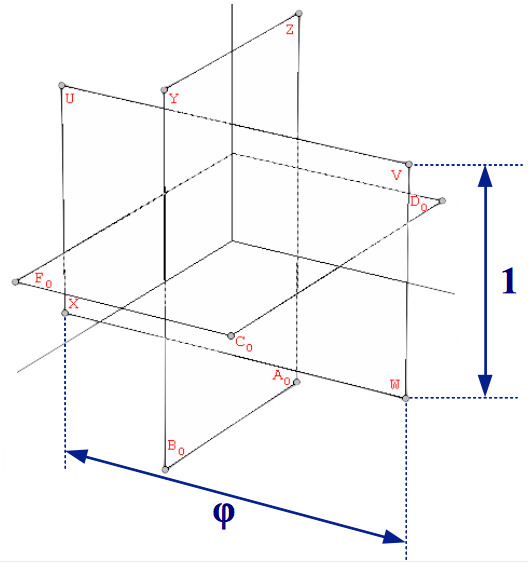
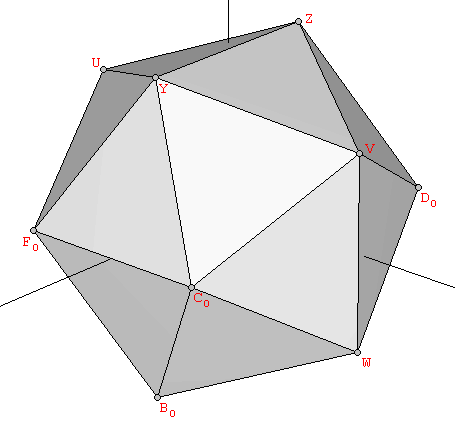
Por contra, si queremos construir los sólidos del segundo grupo, sus vértices en coordenadas cartesianas contienen deben contener la Proporción Aurea. Los vértices del Icosaedro pueden obtenerse fácilmente a partir de tres rectángulos Aureos mútuamente ortogonales, cuyos lados están en proporción 1:φ (la longitud de arista real de todos los poliedros mostrados en las figuras de este artículoes doble de la mostrada por las flechas azules que indican las proporciones Aureas). Las aristas del icosaedro son los segmentos que los vértices de cada rectángulo con sus cinco vecinos más cercanos, como se muestra en la Figura 2 (si, en su lugar, uniéramos cada vértice con los cinco vértices opuestos a esos cinco más cercanos, obtendríamos una bonita estelación del dodecaedro conocida como el pequeño dodecaedro estrellado, véase la Sección 3):
 |
 |
|
| (a) | (b) | |
| Figura 2: Los vértices del icosaedro están definidos por tres rectángulos Aureos mútuamente ortogonales. | ||
 |
||
| Tabla 2: Los vértices del icosaedro en coordenadas cartesianas. |
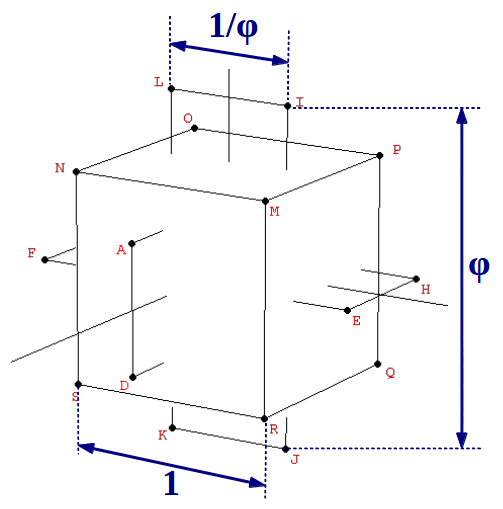
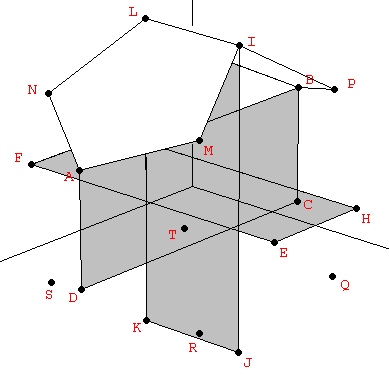
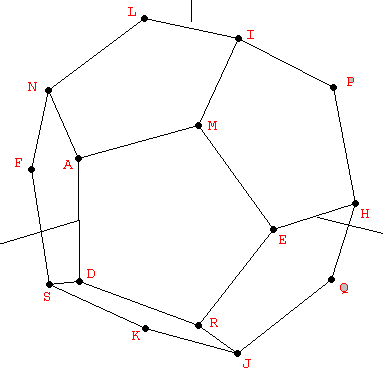
Para construir el dodecaedro, resulta de ayuda saber que el cubo está contenido en su interior. Empezando por los ocho vértices de un cubo, los doce vértices restantes pueden obtenerse a partir de tres rectángulos ortogonales también relacionados con la Proporción Aurea, pero en una proporción 1:φ2 en lugar de 1:φ como en el caso del icosaedro (Figura 3):
 |
 |
 |
| (a) | (b) | (c) |
| Figura 3: Los vértices del dodecaedro pueden obtenerse a partir del cubo y tres rectángulos Aureos mútuamente ortogonales con una relación de lados 1:φ2. | ||
 |
||
| Tabla 3: Los vértices del dodecaedro de la Figura 3, en coordenadas cartesianas. |
3.- La Proporción Aurea en las Estelaciones
3.1.- La Proporción Aurea en el Pequeño Dodecaedro Estrellado
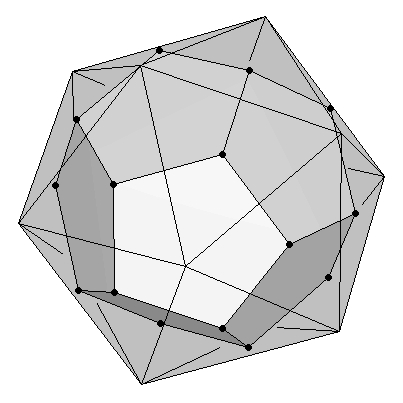
El dodecaedro y el icosaedro son duales el uno del otro. Ello significa que, partiendo de un icosaedro, se puede obtener fácilmente un dodecaedro uniendo los puntos medios de las caras del icosaedro (Figura 4a). Y en sentido contrario, se puede formar un icosaedro uniendo los puntos medios de las caras de un dodecaedro (Figura 4b).
 |
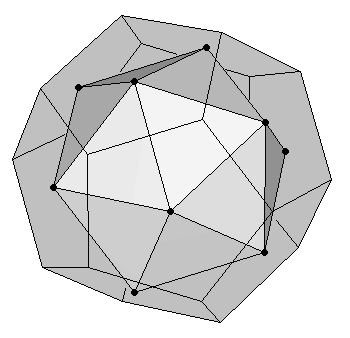 |
| (a) Dodecaedro como dual de un icosaedro | (b) Icosaedro como dual de un dodecaedro |
| Figura 4 | |
De hecho, si un traza doce rectas que partan del centro del dodecaedro y crucen los puntos medios de sus caras, cualquier conjunto de doce puntos ubicados sobre estas rectas y equidistantes del punto central también definirán un icosaedro, aunque a escalas diferentes. Un caso particular muy interesante de este conjunto infinito de icosaedros es el que se obtiene como sigue: tomad un dodecaedro y extended sus aristas hasta que se crucen de nuevo en unos puntos distantes. Encontraréis que todo conjunto de cinco aristas extendidas converge en un punto situado sobre las doce rectas mencionadas más arriba; por lo tanto son los vértices de un icosaedro. Estos vértices también se pueden obtener extendiendo de forma simétrica los lados cortos de los rectángulos que componen el dodecaedro, hasta alcanzar un rectángulo Aureo (Figura 5).
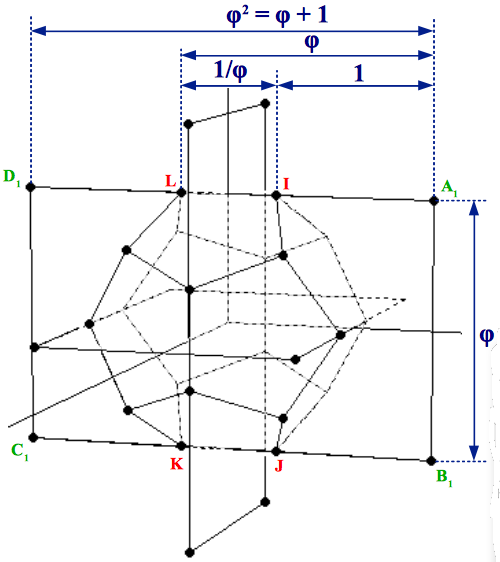 |
||
| Figura 5: Extendiendo los tres rectángulos Aureos de proporción 1:φ del dodecaedro hasta obtener tres rectángulos Aureos de proporción 1:φ2 se llega a los vértices de un icosaedro especial: aquél que da lugar al pequeño dodecaedro estrellado. |
Hay dos hechos interesantes con respecto a este icosaedro especial: el primero de ellos es que tiene una longitud de arista en proporción 1:φ2 respecto a la longitud de arista del dodecaedro original, lo cual puede apreciarse claramente en la figura precedente. Pero el otro hecho destacable es que el proceso de extender las aristas del dodecaedro culmina en una bonita estelación conocida como el Pequeño Dodecaedro Estrellado (Figura 6).
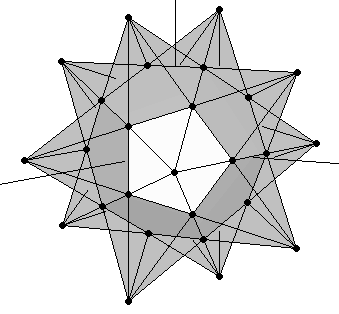 |
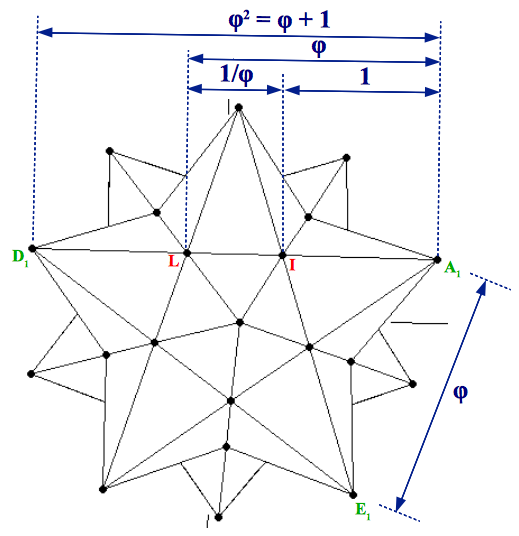 |
| (a) | (b) |
| Figura 6: El pequeño dodecaedro estrellado contiene tres potencias de la proporción Aurea. Eso se aprecia claramente en sus caras pentagramáticas. Sus vértices (exteriores) definen un icosaedro cuya longitud de arista (A1E1) está en proporción 1:φ2 con la arista del dodecaedro original (IL). | |
 |
||
| Tabla 4: Coordenadas cartesianas del pequeño dodecaedro estrellado. Los vértices del dodecaedro original (Tabla 3),aunque visibles, no son vértices de la estelación. |
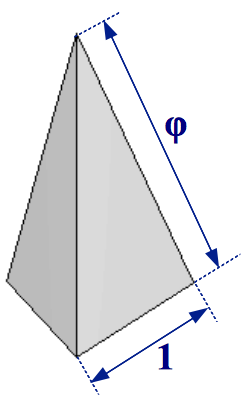
Este sorprendente poliedro no convexo contiene tres potencias de la Proporción Aurea en su interior (Figura 6b). Si la longitud de arista del dodecaedro original se toma como la unidad, el pequeño dodecaedro estrellado puede verse como una extensión de este dodecaedro añadiendo una pirámide Aurea pentagonal a cada una de sus caras. Una pirámide Aurea tiene una apotema en proporción 1:φ con respecto al lado de su base, luego cada una de sus caras laterales son Gnomos Aureos (Figura 7).
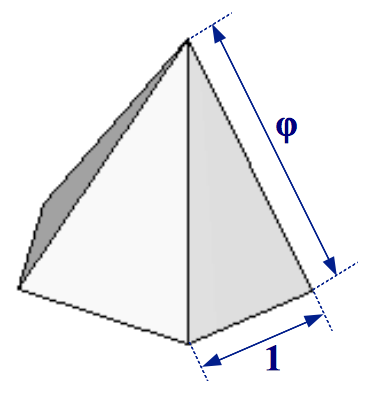 |
 |
|
| (a) Pirámide Aurea pentagonal | (b) Pirámide Aurea Triangular | |
| Figura 7 | ||
3.2.- La Proporción Aurea en el Gran Dodecaedro estrellado
Al igual que sucede con su compañero el pequeño dodecaedro estrellado, existen diversas formas de estudiar la construcción del gran dodecaedro estrellado. Como estelación, es el resultado de extender los vértices de un icosaedro regular hasta que se encuentren en un nuevo conjunto de puntos. ¿Cuántos puntos? Fácil de adivinar: si la estelación del dodecaedro condujo a los 12 vértices de un icosaedro, la estelación del icosaedro conducirá a los 20 vértices de un dodecaedro. Veamos en qué proporción.
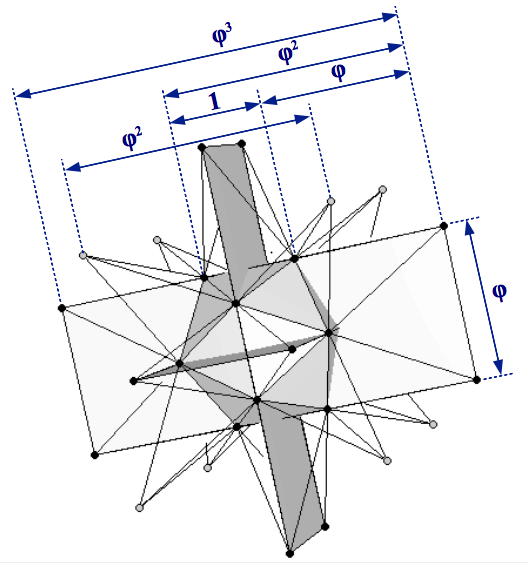 |
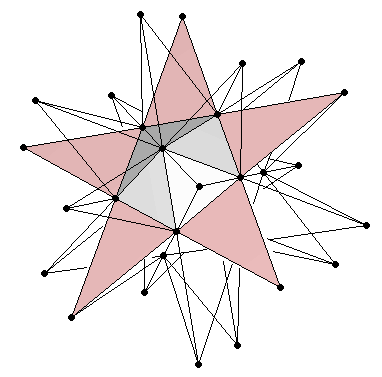 |
| (a) | (b) |
| Figura 8: (a) Construcción del gran dodecaedro estrellado partiendo de un icosaedro de arista unitaria. Los puntos negros más externos describen los rectángulos 1:φ2 de un dodecaedro, mientras que los puntos grises son los vértices de un cubo. (b) La proporciónes Aureas pueden apreciarse claramente en las caras pentagramáticas. | |
El proceso puede dividirse en dos pasos. El primer paso consiste en extender de forma simétrica los tres rectángulos Aureos 1×φ del icosaedro original hasta que formen los tres rectángulos 1:φ2 necesarios para un dodecaedro (Figura 8a). Tomando la longitud de arista del icosaedro como la unidad, las medidas reales de esos rectángulos extendidos serán φ×φ3. Esto se aprecia de forma más clara cuando se observa las caras pentagramáticas del gran dodecaedro estrellado (Figura 8b). Estos rectángulos sólo proporcionan doce de los veinte vértices de un dodecaedro. Tal como hemos visto en la sección 2, los ocho vértices restantes forman un cubo. Siguiendo las proporciones mostradas en la Figura 3 y en la Tabla 3, este cubo debe tener una longitud de arista de φ2 (Figura 8a).
La construcción del gran dodecaedro estrellado también se puede pensar partiendo de un icosaedro y poniendo una pirámide Aurea triangular (Figura 7b) encima de cada una de sus caras. El poliedro estrellado resultante se muestra en la Figura 9.
 |
 |
| (a) | (b) |
| Figura 9: El gran dodecaedro estrellado y su icosaedro interior. | |
 |
||
| Tabla 5: Las coordenadas cartesianas del gran dodecaedro estrellado. Los vértices del icosaedro original (Tabla 2), aunque visibles, no son vértices de la estelación. |
3.3.- El Doble Pentadodecaedro
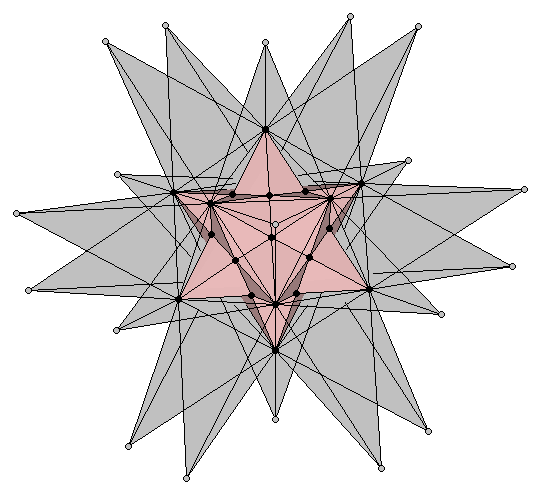
El procedimiento descrito en las dos secciones precedentes también se puede seguir en un orden secuencial: partiendo del dodecaedro, extender sus aristas para formar un pequeño dodecaedro estrellado. Como sus vértices describen un icosaedro, las aristas (imaginarias) de este pueden extenderse hasta obtener el gran dodecaedro estrellado (Figura 10a). El resultado de todo el proceso es un gran dodecaedro estrellado que contiene un pequeño dodecaedro estrellado en su interior (Figura 10b).
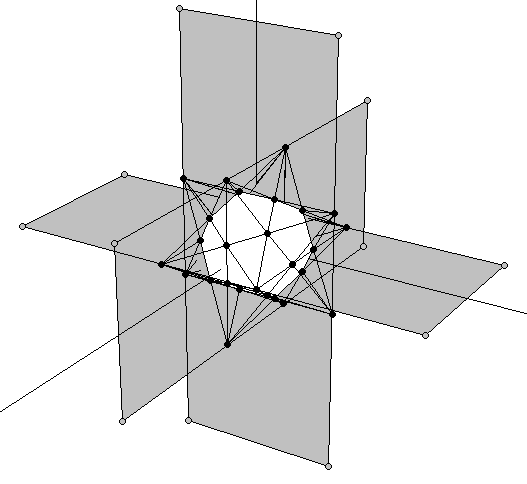 |
 |
| (a) | (b) |
| Figura 10: (a) Extensión de los rectángulos Aureos del pequeño dodecaedro estrellado para formar los rectángulos 1:φ2 de un dodecaedro que describe lo vértices del Doble Pentadodecaedro (bolitas grises). Como se describe en la sección 3.2 (Figura 8) sólo falta añadir los vértices de un último cubo en la proporción adecuada (b) Una vista semitransparente del doble pentadodecaedro que muestra su pequeño dodecaedro estrellado interior. | |
Este poliedro se conoce como Doble Pentadodecaedro. Su nombre proviene del hecho que cada uno de los doce puntos internos del gran dodecaedro estrellado -que coinciden con los vértices del pequeño dodecaedro estrellado contenido en su interior- tiene dos pentagramas asociados con él (el rosa y el azul que se destacan en la Figura 11). Resulta destacable el hecho de que el doble pentadodecaedro contiene cinco potencias de la Proporción Aurea (Figura 11).
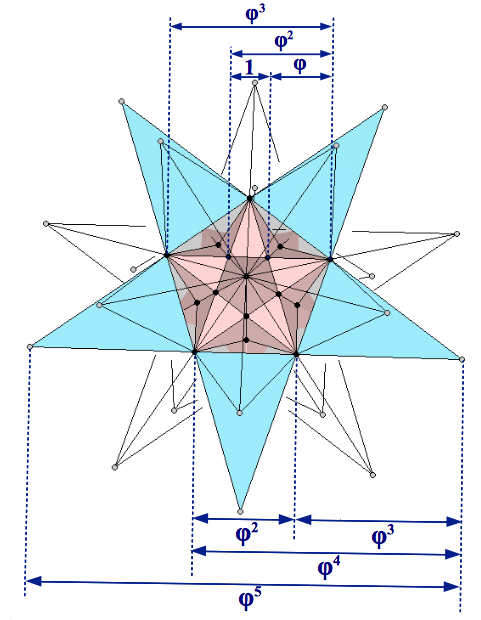 |
| Figura 11: El doble pentadodecaedro tiene un pequeño dodecaedro estrellado en su interior, cada uno de cuyos 12 vértices tiene asociados 2 pentagramas (destacados en rosa y azul en la figura). Nótese que esta doble estelación contiene 5 potencias de la Proporción Aurea. |
Algunos autores mantienen que el doble pentadodecaedro describe la nueva red energética cristlina que está activando en estos momentos en nuestro planeta Tierra. Esta red se supone que nos debe permitir un mayor acceso a las dimensiones no físicas que existen por encima de nuestra realidad tridimensional.
4.- La Proporción Aurea y el Triacontaedro Rómbico
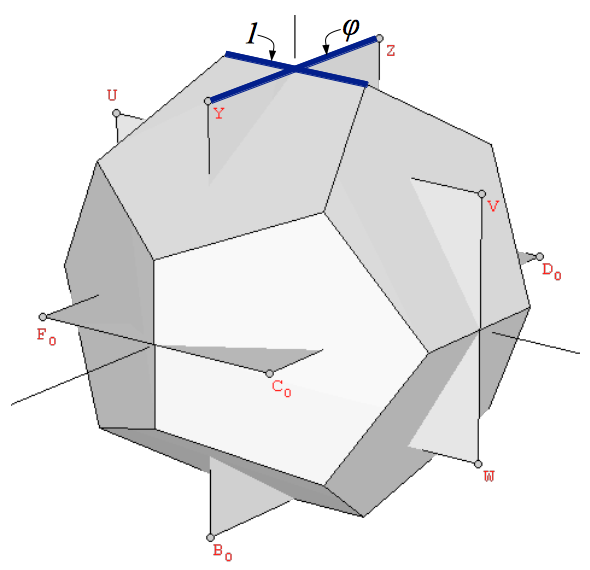
¿Cuál es el resultado de juntar los vértices de un dodecaedro y de un icosaedro, ambos a la misma escala? Depende de su orientación relativa. Decimos que un dodecaedro y un icosaedro están en la misma escala cuando el lado largo de sus rectángulos Aureos constituyentes (de proporciones 1:φ2 y 1:φ) tiene la misma longitud. Dos poliedros que cumplen este primer requerimiento pueden orientarse de muchas formas diferentes el uno en relación al otro. La orientación clave es aquella en la que los tres rectángulos aureos del icosaedro y el dodecaedro son exactamente ortogonales el uno al otro, y tienen sus lados largos paralelos (Figura 12).
 |
 |
| (a) | (b) |
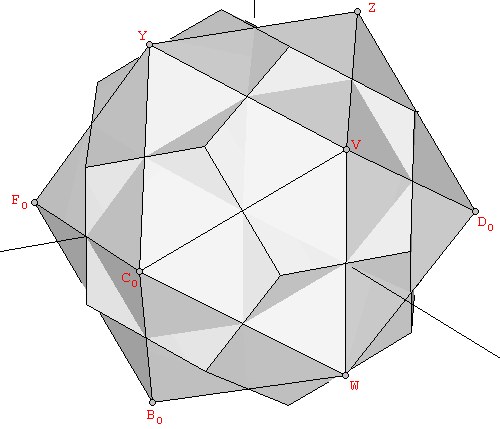
| Figura 12: (a) Decimos que un icosaedro y un dodecaedro están a la misma escala cuando el lado lardo (vertical en la figura) de sus rectángulos Aureos constituyentes tiene la misma longitud. (b) El poliedro resultante de la superposición de un dodecaedro y un icosaedro a la misma escala. Podemos ver que las 30 aristas de ambos poliedros son ortogonales la una a la otra y definen las diagonales de 30 rombos Aureos. | |
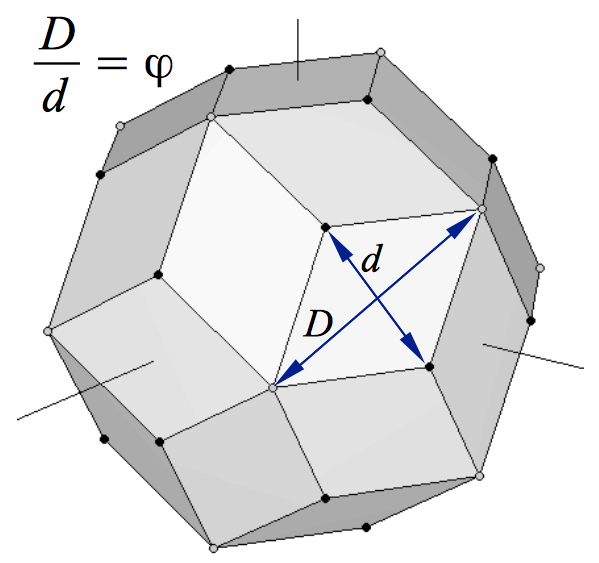
Los dos requerimientos precedentes resultan cumplirse de forma exacta por el dodecaedro y el icosaedro mostrados en las Figuras 2 y 3, cuyas coordenadas se recogen en las Tablas 2 y 3. En este caso, el lado largo coincidente de los rectángulos Aureos tiene una longitud común de 2φ. Si superponemos los dos poliedros, obtenemos un poliedro no convexo (Figura 12b). Podemos observar en la Figura 12 que los lados cortos de cada par de rectángulos Aureos del dodecahedro-icosaedro están en Proporción Aurea (en este caso, sus longitudes son 2/φ y 2). Constituyen las dos diagonales de un rombo Aureo. De hecho, la Figura 12b muestra que todas las aristas coplanares de nuestros dodecaedro e icosaedro intersectan de forma ortogonal definiendo 30 rombos Aureos. Por último, si formamos el poliedro convexo que une todos sus vértices, el resultado es un Triacontaedro Rómbico (Figura 13).
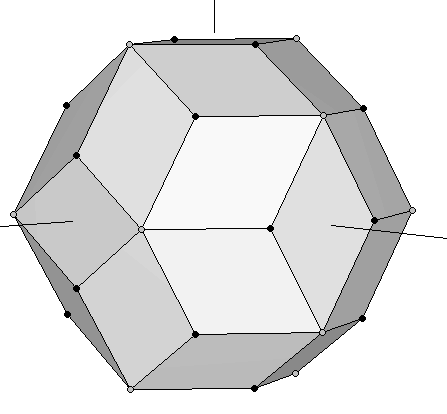 |
 |
| (a) | (b) |
| Figura 13: Triacontaedro Rómbico formado uniendo un dodecaedro y un icosaedro a la misma escala. Los vértices del dodecaedro original son las bolitas negras, mientras que las bolitas grises son los vértices del icosaedro. | |
Con nuestro proceso de construcción, hemos establecido que las 30 caras de un triacontaedro rómbico son rombos Aureos cuyas diagonales corta y larga definen las aristas de un dodecaedro y un icosaedro, respectivamente. El triacontaedro rómbico es un poliedro semiregular cuyos vértices definen casi todos los Sólidos Platónicos, porque el cubo está contenido dentro del dodecaedro, y el tetraedro está contenido dentro del cubo (Figuras 1 y 3). Aunque algunos autores afirman que también contiene el octaedro, no es estrictamente cierto. Para hacerlo "aparecer" necesitaríamos añadir los puntos centrales de las caras del cubo, que no son vértices del triacontraedro rómbico. El poliedro siguiente soluciona este problema.
5.- El Poliedro 120
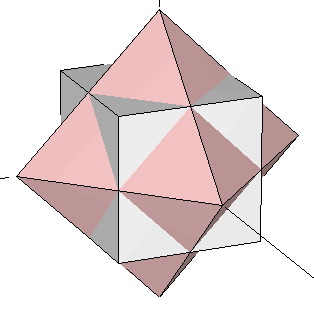
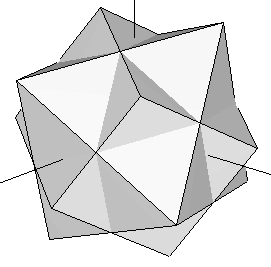
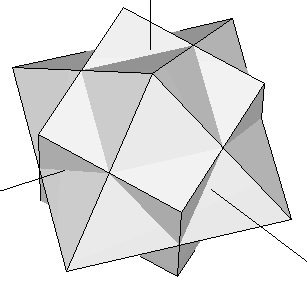
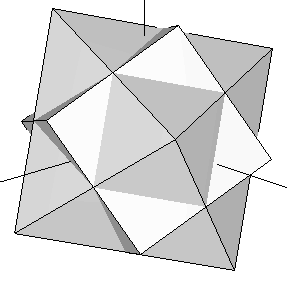
Vamos a coger el cubo contanido en nuestro dodecaedro original (Figura 3) y unirlo con un octaedro cuyas aristas intersectan las del cubo exactamente en su punto medio (es decir, unimos el cubo de la Figura 1b con el octaedro de la Figura 1a). Ahora rotamos el complejo hasta que el cubo coincide con otro onjunto de ocho vértices del dodecaedro que lo contiene. Este proceso puede hacerse de cuatro formas diferentes. El conjunto de vértices resultante de los cinco cubos define el dodecaedro (algunos vértices están repetidos). Si añadimos, a la misma escala, nuestro icosaedro a este dodecaedro, obtenemos el triacontaedro rómbico estudiado en la sección precedente (Figura 13). El conjunto de 30 vértices de nuestros cinco octaedros resultan caer justo encima de cada uno de los rombos Aureos de ese triacontaedro rómbico. Sus coordenadas se muestran en la Tabla 6 más abajo.
 |
 |
 |
 |
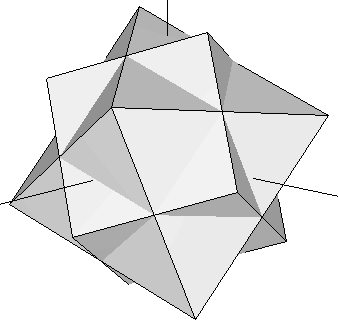 |
| Figura 14: Superposición del octaedro y el cubo de la Figura 1. En cada paso en este proceso, se rota el complejo hasta que el cubo encaja con un nuevo conjunto de ocho vértices del dodecaedro que lo contiene. El octaedro rota al unisono, definiendo un conjunto de 6 nuevos vértices en cada paso (ver Tabla 6). | ||||
 |
||
| Tabla 6: Las coordenadas cartesianas de los cinco octaedros rotados mostrados en la Figura 14. |
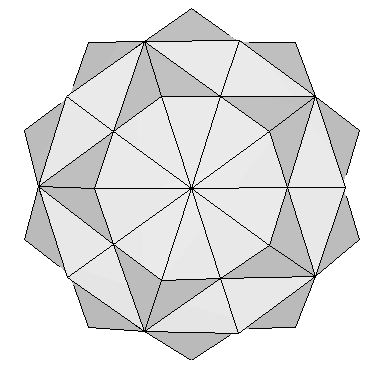
Uniendo los 20 vértices del dodecaedro y los 12 vértices del icosaedro, tenemos los 32 vértices del triacontaedro (Figuras 12 y 13). Ahora a este conjunto le añadimos los 30 vértices de los octaedros precedentes. El resultado final es un conjunto de 62 vértices que define un bonito poliedro no convexo conocido como el Poliedro 120 (Figura 15):
 |
 |
 |
| (a) | (b) | (c) |
| Figura 15: Tres vistas diferentes del poliedro 120. Contiene los vértices del dodecaedro, del icosaedro, y de los cinco octaedros rotados. | ||
Este poliedro ha sido estudiado extensamente por Robert W. Ray. Tiene 120 caras, porque cada una de las 30 caras faces del triacontaedro rómbico ha sido "aumentada" por una pequeña pirámide de cuatro lados. Estas 30 pirámides tienen dimensiones muy especiales. No sólo su base es un rombo Aureo, sino que el lado de su base también está en Proporción Aurea con su apotema más corta. Esto se puede demostrar fácilmente a partir de las coordenadas de las Tablas 2, 3 y 6 como sigue:
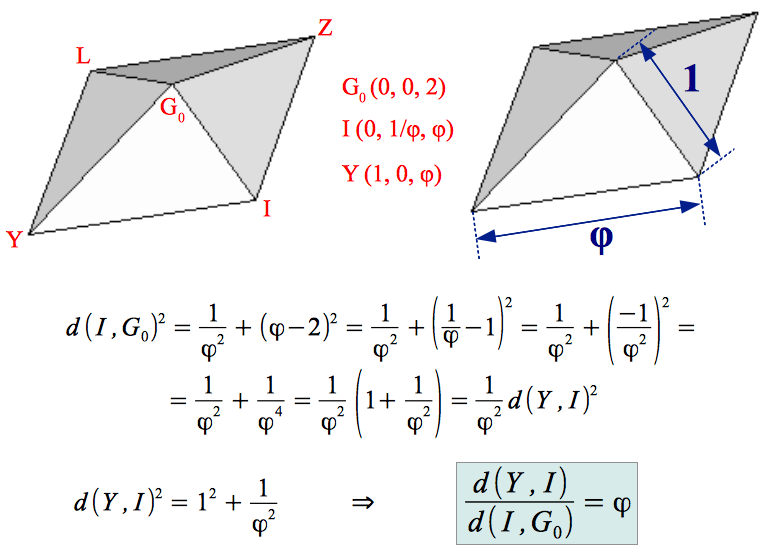
6.- Sobre la estabilidad estructural
Los poliedros que hemos examinado en este artículo se dividen en dos grandes grupos. Al primer grupo pertenecen el tetraedro, el octaedro y el cubo. Ellos tienen en común el hecho de que sus coordenadas cartesianas tienen valores enteros. Por lo tanto estos poliedros pueden representarse de forma exacta en un ordenador. Por otro lado, la mayoría de poliedros examinados en este artículo pertenecen al segundo grupo: son aquellos cuyas coordenadas involucran la Proporción Aurea. Estos poliedros no pueden representarse de forma exacta en un ordenador. Las coordenadas que hemos usado para nuestros dibujos son exactas hasta diez cifras decimales, pero la Proporción Aurea tiene un número infinit de cifras decimales. Este hecho no impide su construcción física exacta. Por ejemplo, el icosaedro puede construirse con un conjunto de treinta bastones idénticos y doce conectoreso.
Pero si uno intenta construir todos esos poliedros, le resultará evidente aque algunos de ellos no son estructuralmente estables. El ejemplo más simple es el cubo: si alguna vez has intentado construir un cubo con cualquier tipo de bastones rígidos y conectores rotatorios, te habrás dado cuenta que se colapsa. Lo mismo sucede con el doecaedro. Ambos pueden estabilizarse añadiendo aristas adicionales que conecten sus aristas entre ellas. Por ejemplo el cubo puede estabilizarse uniendo sus vértices con dos tetraedros entrelazados (ver Figura 1d), y el dodecaedro uniendo sus vértices desde el interior en la forma de un gran dodecaedro estrellado (ver Figuras 8 y 9), o hacia el exterior formando un pequeño dodecaedro estrellado (ver Figura 6). En cualquier caso, el poliedro resultante no "contiene" las caras ni del cubo ni del dodecaedro. A partir de esta observación, se puede hacer la conjetura de que estas estructuras podrían tener una naturaleza energética (sutil). Un cubo puede "verse" simepre que está presente un octaedro estrellado, mientras que el dodecaedron puede "observarse" siempre que está presente una estructura icosaédrica -ya sea un pequeño o un gran dodecaedro estrellado. De hecho, Buckminster Fuller ya estableció que la condición suficiente y necesaria para que una construcción física sea estructuralmente estable es que sea triangulada -de aquí la estabilidad del tetraedro, octaedro e icosaedro.
