- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Phi en la Gran Pirámide
1.- Introducción
La Gran Pirámide de Giza, en Egipto, nos fascina a muchos. Es una construcción sorprendente con una precisión increible, mucho mayor de la que se puede conseguir con nuestra tecnología actual. Es este artículo discutimos algunas propiedades importantes de su diseño que están directamente relacionadas con la Geometría Sagrada. Vamos a mostrar que el cociente de su apotema respecto a la mitad de su base obedece a la Razón Aurea, y que el perímetro de su base es igual al de un círculo con radio igual a su altura. Vamos a ver también que los ángulos de la Gran Pirámide esconden el número de Euler. Como preparación necesitamos recordar las propiedades del triángulo de Kepler, así como el problema de la Cuadratura del Círculo. A continuación mostraremos que las dimensiones de la Tierra y la Luna obedecen a las mismas proporciones que las dimensiones de la Gran Pirámide, y que pueden obtenerse directamente usando el triángulo de Pitágoras 3-4-5. Y por último mostraremos que las dimensiones exactas de la Gran Pirámide responden a una fórmula sencilla relacionada con los cubos de determinados números enteros.

2.- La Cuadratura del Círculo
Considérese un triángulo rectángulo genérico con base b, altura h e hipotenusa a. Su circunferencia circunscrita tendrá el mismo perímetro que un cuadrado de lado h siempre que los lados del triángulo obedezcan a la relación (Figura 1a)
Esto se conoce a menudo como la Cuadratura del Círculo. Si el cuadrado se forma con el lado igual al doble de la base del triángulo, el mismo problema se suele plantear en términos del círculo que tiene un radio igual a la altura h del triángulo (Figura 1b). En este caso, la cuadratura del círculo se consigue si la altura y la base del triángulo están relacionadas como
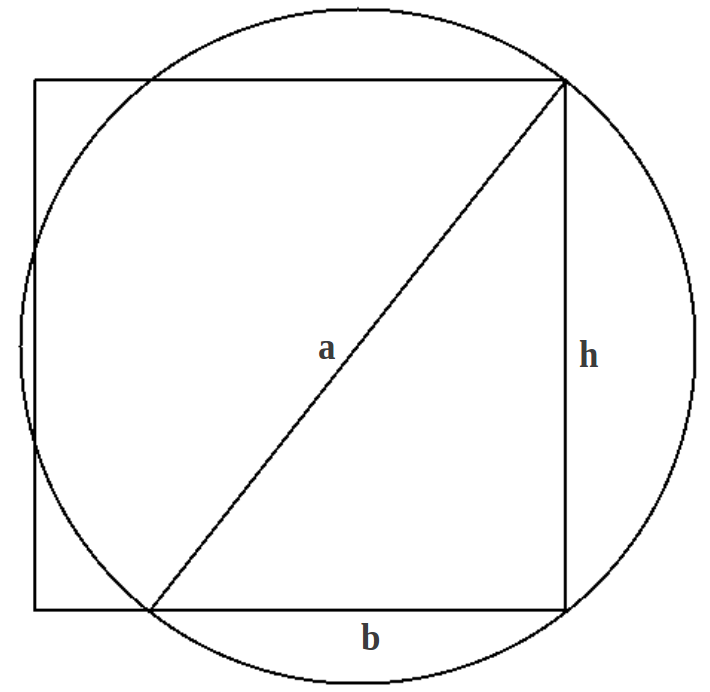 |
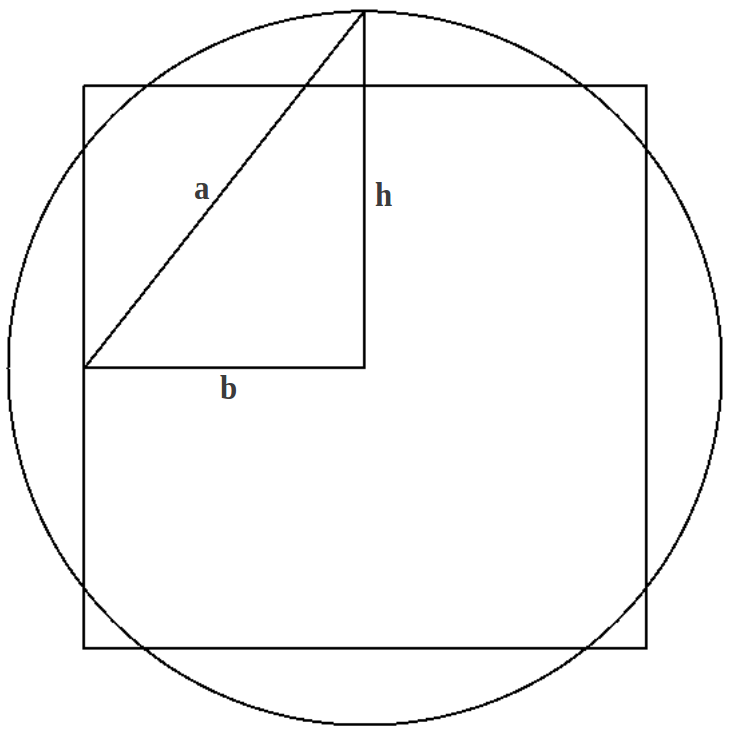 |
| (a) | (b) |
| Figure 1: Dos formas de conseguir la cuadratura del círculo partiendo del mismo triángulo rectángulo. | |
Resulta obvio que las dos relaciones anteriores no se pueden satisfacer simultáneamente, porque dados dos lados de un triángulo rectángulo el tercer lado debe obedecer el Teorema de Pitágoras. Sin embargo, si relajamos las igualdades anteriores a buenas aproximaciones, vemos que los lados del triángulo tendrían que estar relacionados según una progresión geométrica:
De forma natural surge la cuestión: ¿es eso posible? Y en caso afirmativo, ¿cuál es la precisión de la cuadratura del círculo conseguida de esa forma?
3.- El triángulo de Kepler
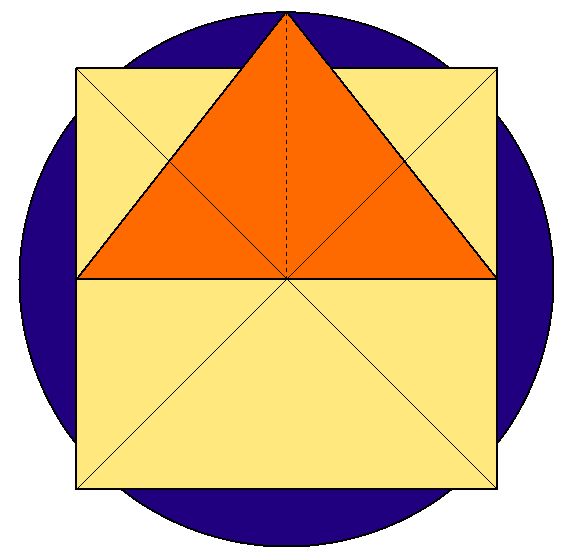
Sabemos que existe un sólo triángulo rectángulo cuyos lados están en progresión aritmética, el triángulo 3-4-5 de Pitágoras. De forma similar, existe un único triángulo rectángulo cuyos lados están en progresión geométrica, conocido como el triángulo de Kepler. ¿Adivinas qué número mágico rige este triángulo? Sí, como no podía ser de otra forma ¡es la Razón Aurea! Los lados del triángulo de Kepler obedecen a la progresión . El lector puede comprobar que este triángulo aproxima la Cuadratura del Círculo con un error del 0.096% (Figura 2), lo cual ejemplifica la conocida relación entre π y φ:
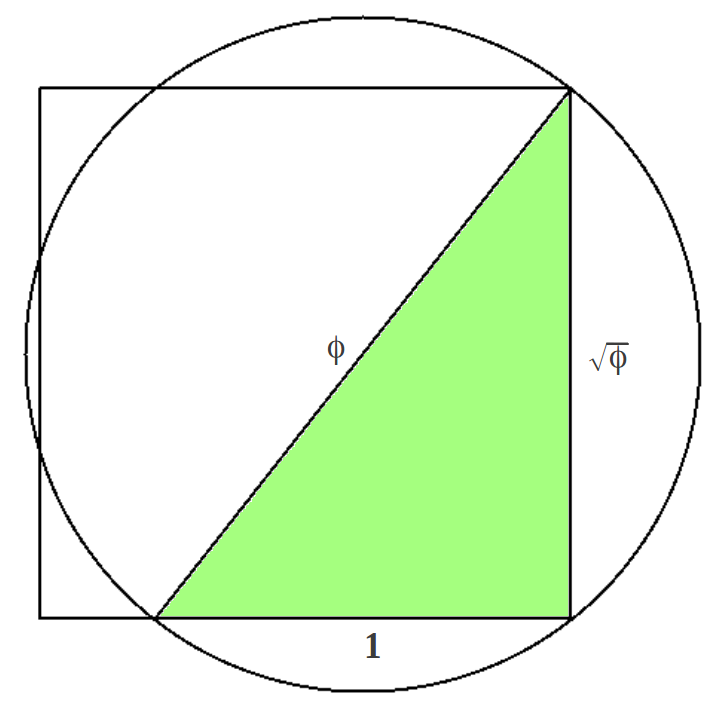 |
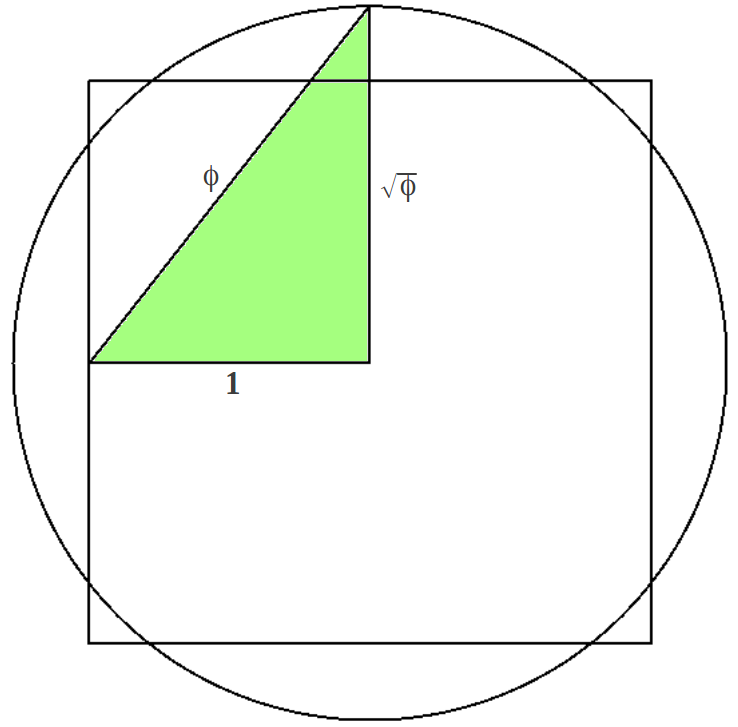 |
| Figura 2: La cuadratura del círculo en el triángulo de Kepler. | |
En la próxima sección vamos a mostrar que la Gran Pirámide cuadra el círculo con una aproximación mejor que la que se obtiene con el triángulo de Kepler.
4.- Geometría Sagrada en la Gran Pirámide
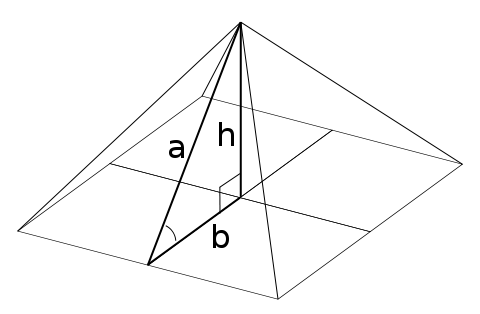
La figura siguiente muestra la definición del apotema (a), la altura (h) y la semibase (h) de una pirámide cuadrangular típica. A su derecha listamos las dimensiones aceptadas de la Gran Pirámide en tres unidades de medida distintas:
 |
2b | h |
| 440 ec | 280 ec | |
| 755.9 ft | 481.0 ft | |
| 230.4 m | 146.6 m | |
| Tabla 1: Dimensiones aceptadas de la Gran Pirámide de Giza (de Wikipedia), dadas en codos egipcios (ec), en pies (ft) y en metros (m). | ||
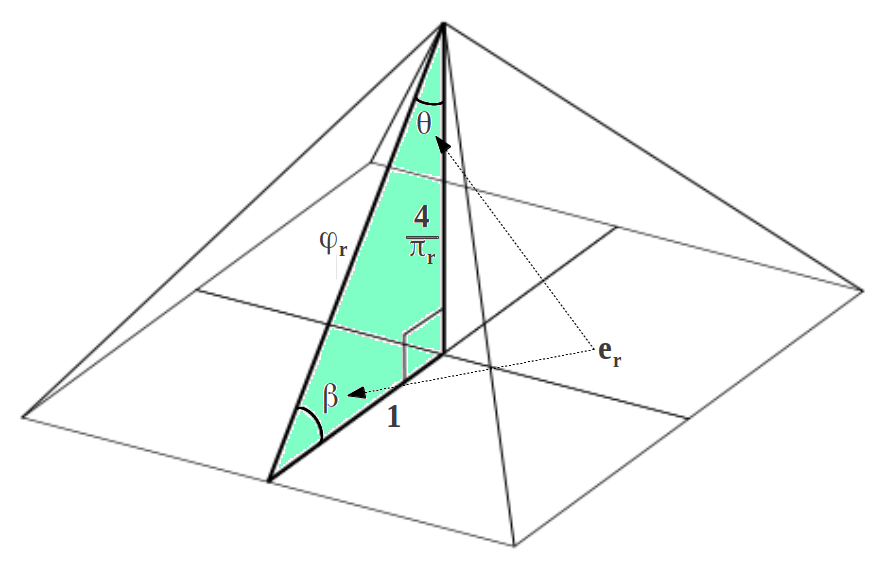
La primera propiedad que queremos destacar es la presencia de la Razón Aurea en la Gran Pirámide con una gran precisión, como el cociente de la apotema respecto a la semibase:
Este cociente proporciona una aproximación φr de la Razón Aurea φ. Como consecuencia, el triángulo a-b-h mostrado en la Tabla 1 es muy parecido al triángulo de Kepler. Por lo tanto, ¡la Gran Pirámide también ejemplifica en piedra la Cuadratura del Círculo! Si dibujamos un círculo con radio igual a su altura, su perímetro será el mismo que el de la base de la pirámide con un error de tan sólo el 0.04%:
El hecho de que la Gran Pirámide aproxime la Cuadratura del Círculo con una precisión mejor que el triángulo de Kepler se debe al uso de la aproximación racional de π/2 en el cociente entre la altura y la base (Figura 3):
Así pues la aproximación racional πr de π viene dada por:
 |
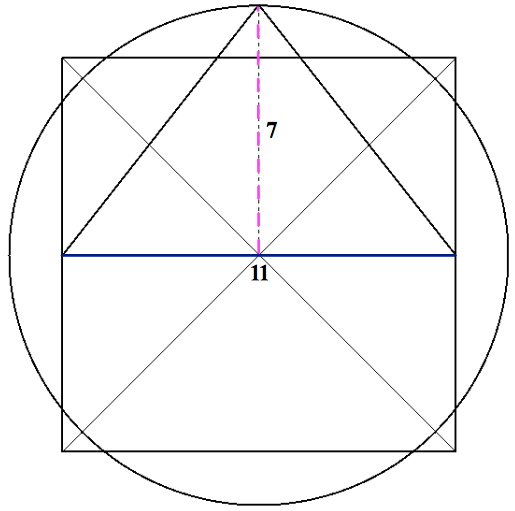 |
| (a) Cuadratura del círculo en la Gran Pirámide | (b) Aproximación racional de π/2 en la relación de altura a base de la Gran Pirámide. |
| Figura 3 | |
Menos conocido es el hecho de que las dimensiones de la Gran Pirámide esconden también otro número importante para la ciencia, el número de Euler. La investigación de Rick Howard ha mostrado que el cociente de los dos ángulos del triángulo a-b-h de la Gran Pirámide (Tabla 1) proporciona una aproximación muy precisa er de e:
La tabla siguiente ilustra y resume los tres números claves contenidos en las dimensiones de la Gran Pirámide de Giza:
 |
Número Clave | Valor Exacto | Gran Pirámide | Error |
| φ | 1.618033989 | 1.618590347 | 0.034% | |
| π | 3.141592653 | 3.142857153 | 0.040% | |
| e | 2.718281828 | 2.717323980 | 0.035% | |
| Tabla 2: Números clave escondidos en las dimensiones de la Gran Pirámide de Giza. | ||||
5.- La Gran Pirámide contiene el diámetro de la Tierra y la Luna
Si lo anterior no ha dejado al lector sorprendido, lo que sigue probablemente lo hará. La cuadratura del círculo en la Gran Pirámide de Giza como se muestra en la Figura 3a es un diagrama que permite la determinación precisa del diámetro tanto de la Tierra como de la Luna. Tan "sólo" se necesita dibujar un círculo inscrito dentro del cuadrado (la Tierra) y un pequeño círculo centrado en el ápice y tangente al anterior (la Luna). En cada lado encima de ellos se forman dos triángulos de Pitágoras 3-4-5 exactos (Figura 4).
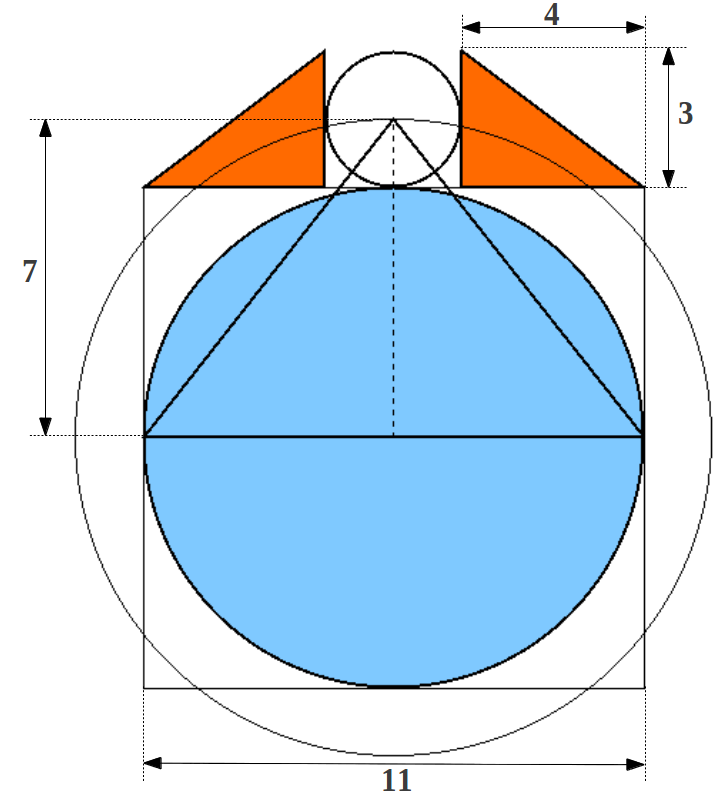 |
| Figura 4: Las proporciones de la Gran Pirámide junto con el triángulo de Pitágoras 3-4-5 conducen a las dimensiones exactas de la Tierra y la Luna (véase también la Figura 5). |
El conocido triángulo 3-4-5 nos permite calcular el número "mágico" 720 como sigue:
A partir de él y de las proporciones de la Gran Pirámide como se muestran en la Figura 4, ¡¡¡puede calcularse directamente el diámetro de la Tierra y de la Luna en millas!!!
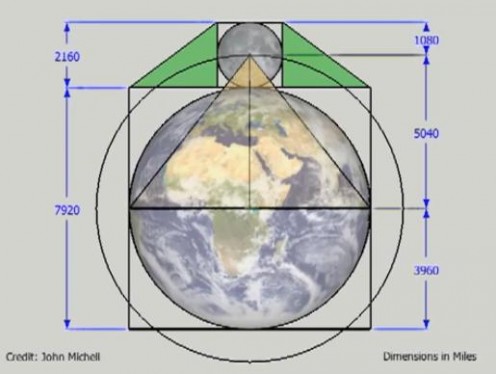
6.- Los arquitectos de la Gran Pirámide tenían un secreto
Siguiendo este excelente artículo de Joseph Turbeville, en esta sección vamosa mostrar como las dimensiones exactas de la Gran Pirámide obedecen a una fórmula muy simple relacionada con los cubos de unos números enteros determinados. Esos valores pueden obtenerse fácilmente a partir de la disposición adecuada de los primeros ocho dígitos de nuestro sistema de numeración y sus múltiples, siempre que se conozcan las unidades adecuadas.
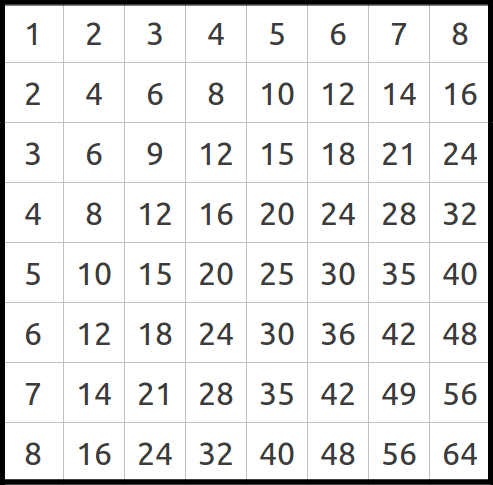
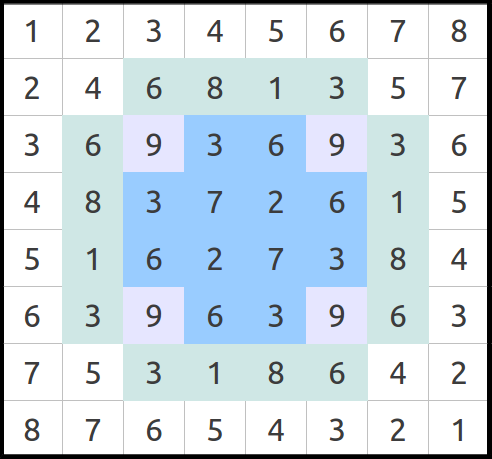
Considérese la Tabla 3a. Cada fila después de la primera se forma multiplicando la primera fila por el número de fila. De esta forma, la segunda fila es dos veces la primera, la tercera es tres veces la primera, etc. El siguiente paso consiste en reducir cada número a un sólo dígito mediante sumas consecutivas, un proceso a veces también llamado destilación (Tabla 3b). En la Tabla 3b hemos destacado las celdas clave que nos permitirán calcular las dimensiones de la Gran Pirámide.
 |
 |
|
| (a) Los primeros ocho números y sus múltiplos. Cada fila se calcula como la primera fila multiplicada por el número de fila. | (b) Reducción de los números de la tabla anterior a un sólo dígito. Hemos destacado los números que permiten clacular las dimensiones de la Gran Pirámide. | |
| Tabla 3 | ||
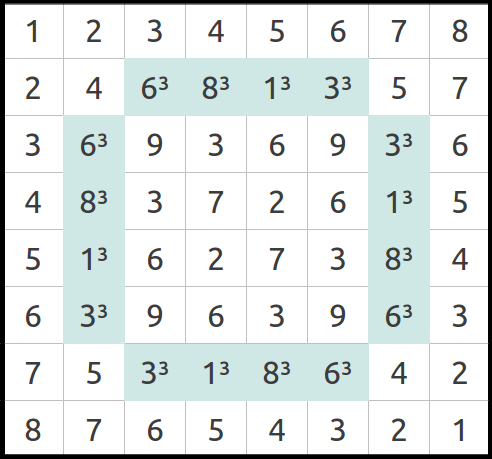
Ahora los cubos de los cuatro números de cualquiera de las líneas de alrededor (Tabla 4a) se suman para obtener el primer número clave:
Reconoces este número? Sí, usando el pié como unidad, esta es exactamente la longitud de la base de la Gran Pirámide.
 |
 |
|
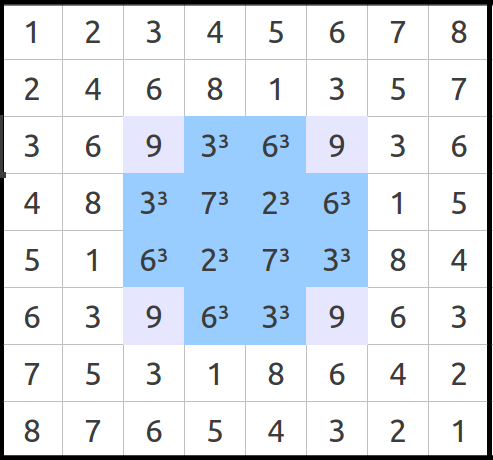
| (a) Sumando los cubos de cualquiera de las líneas destacadas proporciona la longitud de la base de la Gran Pirámide en pies. | (b) Sumando los cubos de cualquier línea de la cruz azul se obtiene el cociente exacto 4/πr. | |
| Tabla 4 | ||
A continuación, cualquiera de las líneas de la cruz azul central (Tabla 4b) proporciona el segundo número clave, de nuevo después de sumar sus cubos:
Si este número parece no tener ningún significado, fijémonos a dónde nos conduce el cociente de ambos:
Como se puede ver, se trata de la proporción exacta que permite calcular la altura de la Gran Pirámide a partir de su semibase:
7. Conclusiones
En la Gran Pirámide de Egipto hay mucha más información codificada que la que hemos resumido en este artículo. Animamos al lector a realizar su propia búsqueda de información. A un nivel astronómico mayor, se sabe que la Gran Pirámide esconde el ciclo de Precesión de los Equinoccios de nuestro sistema solar alrededor del sol central de las Pléyades (25827.5 años) en varias de sus dimensiones (por ejemplo en la suma de las diagonales de su base expresadas en pulgadas piramidales). También es ámpliamente conocido que las tres pirámides del complejo de Giza están alineadas con las estrellas del Cinturón de Orión. A partir de todo lo precedente, parece que podemos extraer una sola conclusión: los arquitectos de la Gran Pirámide de Giza fueron seres extremadamente sabios, con unos conocimientos avanzados de matemáticas y de astronomía que iban mucho más allá del estándar de su tiempo, y hasta me atrevería a decir que más allá de nuestro conocimiento actual.
