- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Phi in Particle Physics
1.- Introduction
In this article I am going to introduce the main results of a new theory of elemetary particle physics developed by the engineer M.S. El Nachie. This theory provides a fractal model of quantum space-time, the so-called E-infinity space, that allows the precise determination of the mass-energy of most elementary particles -and much more- in close agreement with their experimental values. The Golden Ratio emerges naturally in this theory, and turns out to be the central piece that connects the fractal dimension of quantum space-time with the mass-energy of every fundamental particle, and also with several fundamental physical quantities such as the Fine Structure constant. El Nachie has been severely criticised by his non-orthodoxal publication methods -he uses to publish his papers in a Journal where he is the editor in chief. Despite this fact, I think that his theory deserves consideration so I will try to summarize it in the lines that follow.
2.- A simple puzzle with profound implications
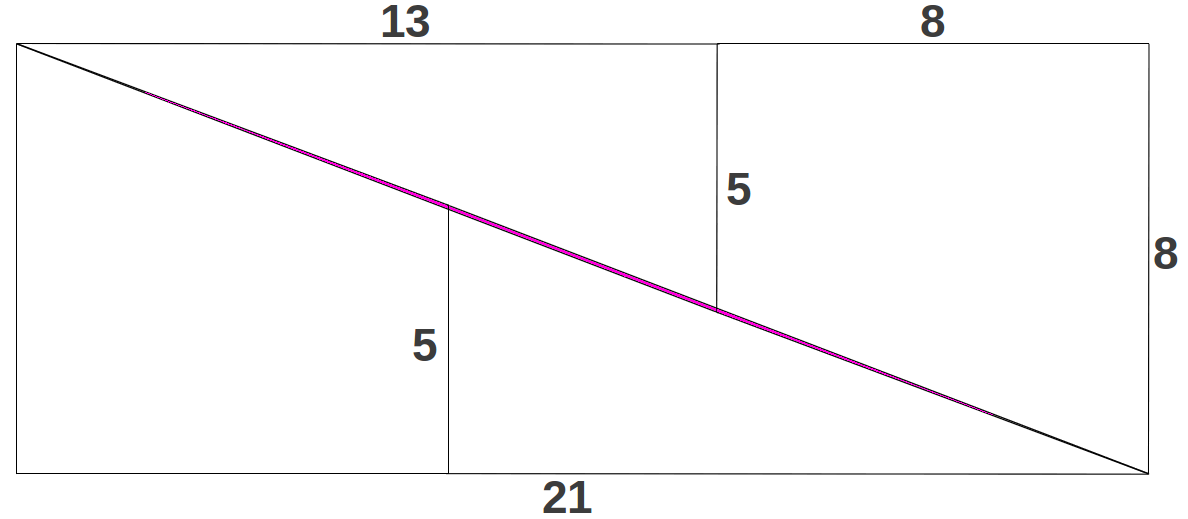
Before entering into the details of the theory, I would like to introduce it by means of a simple geometric puzzle that elegantly summarizes its core results. Consider the following 13x13 square divided into two triangles and two quadrilateral polygons as follows (Figure 1, left). If the four pieces are restructured in the form of a rectangle as shown at the right in Figure 1, it appears that the overall area has inexplicably lost one unit!! What has happened?
 |
| Figure 1: A simple geometrical transformation that apparently should be area-preserving. |
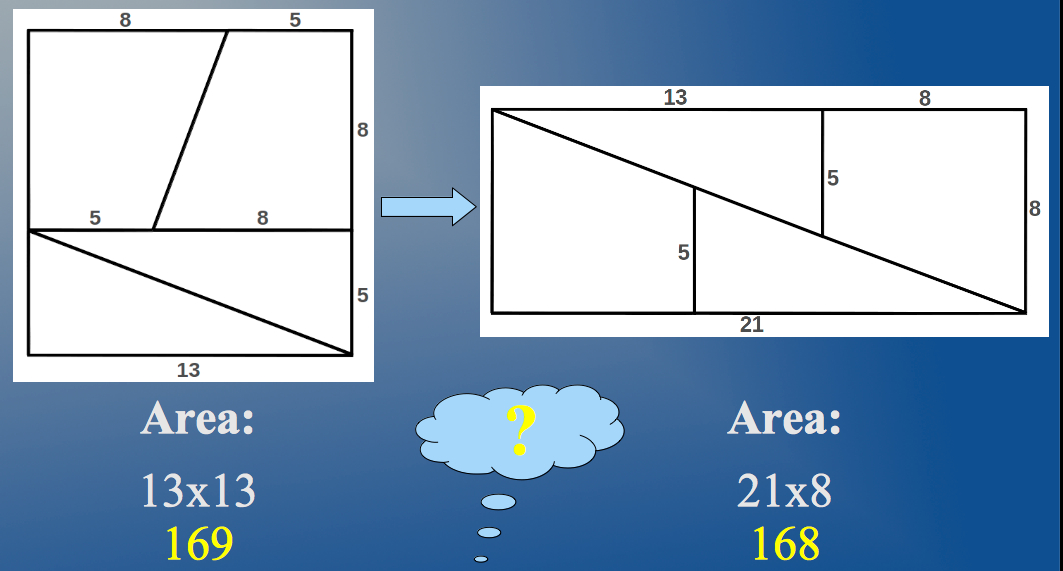
If you don't figure out what happened, you may take look at the bottom of this page later. Notice that the divisions in the original square have been done according to some Fibonacci numbers: 5, 8 and 13=5+8; therefore the sides of the transformed rectangle are also Fibonacci numbers because it has been constructed additively. Now, do you guess how could we correct the dimensions of the initial square so that the above transformation into a rectangle was area-preserving? Yes, as it could not be another way round, we need to introduce the Golden Ratio! If the pieces of the square are constructed according to Golden proportions, then the area of the resulting rectangle will coincide with the area of the square, as it happens in the general case shown below:
 |
| Figure 2: The above transformation is area-preserving when the pieces in the square are proportioned according to the Golden Ratio. |
The exact resulting area can also be expressed as a continuous fraction expansion of the number 7 as follows:
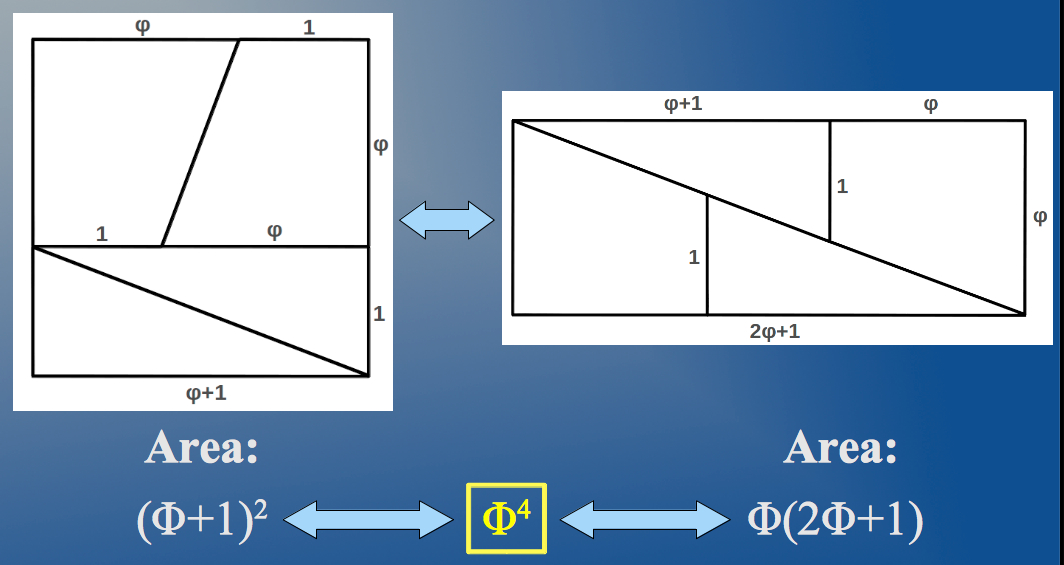
This expression suggests that the involvement of φ into the problem opens the door to self-similar, multiple scale or fractal behaviour. The corrected version of our original puzzle is shown in Figure 3. It is interesting to observe that the correction amounts to a small value k which turns out to be easily expressible in terms of φ, and also as a continuous fraction expansion in this case of number 11:
 |
| Figure 3: The original square in Figure 1 divided according to Golden proportions. |
At this point, the reader may be wondering what on earth does all this stuff have to do with particle physics and the quantum world. Well, I would answer: more than we could initially suspect! The only thing left to do to the corrected version of the puzzle is doubling every length as shown in Figure 4. The resulting polygons have an area that equals five times the theoretical value of the Fine Structure constant, one of the most fundamental and misterious quantities of physics. This is the theoretically correct value proposed by El Nachie. To obtain the experimentally measured value, he argues that one simply needs to add a correction due to the symmetry breaking of the time axis, which in the quantum world is spacialised but in our ordinary world it is not (see Section 3 for details):
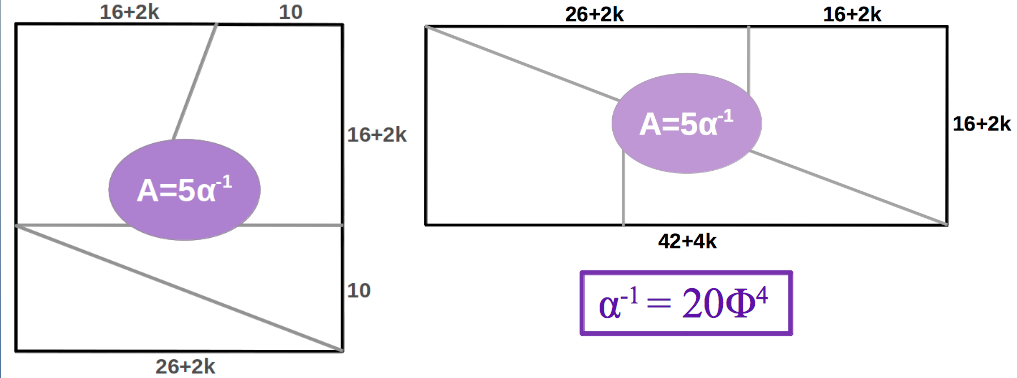 |
| Figure 4: The polygons corrected according to the Golden Ratio proportions and with double edge sizes have an area A=685.4101965, exactly equal to five times the theoretical value proposed by El Nachie for the Fine Structure constant α-1=137.082039, one of the most fundamental and mysterious quantities of Physics. |
But the information contained in these polygons in much more than this. The numbers that appear in the fragments of the polygons form a Fibonacci-like sequence that can be iterated backwards and forwards. If we iterate it two steps backwards, we obtain two more figures that complete another big piece of information: according to El Nachie, they provide the exact values of the (fractally corrected) dimensions of the heterotic string theory, whose conventionally accepted values are 4,6,10,16 and 26:
In addition, some of these values have another meaning as the constants of symmetrical and non-symmetrical unification of all (five) fundamental forces known to current Physics (see more details on section 5).
Before closing this section, I would like to provide my own personal interpretation of the whole picture. It can be seen as if we were watching a "movie" in which the fundamental players are numbers 3, 5 and φ, and the secondary player is number 11. These players are related as follows:
 |
| Figure 5: The relationship among the players involved in the "movie" that describes the transition from ordinary space-time to quantum space-time. |
The first two players 3 and 5 generate the well known Fibonacci sequence, which is involved in the structure of all living forms of our ordinary 3+1 finite dimensional world, from plant growth to the structure of our own human body. The intervention of the third player φ generates a related Fibonacci-like sequence (Figure 6) whose elements contain a small fractal correction k (in El Nachie's theory k is called transfinite correction). The function of fractal correction k is played by the fourth player, namely number 11, which acts as a kind of synchronizer in the form of a continuous fraction expansion (Fig. 5):
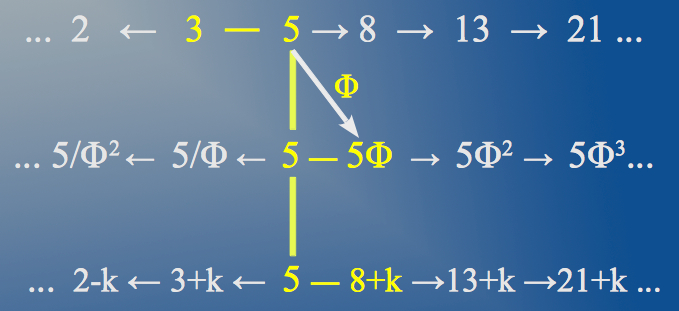 |
| Figure 6: Numbers 3 and 5 generate the conventional Fibonacci sequence, which is present at the core of all living organisms. After the intervention of φ, a Fibonacci-like sequence with a small fractall correction is produced, which (when doubled) contains detailed information about the quantum world. |
The intervention of the Golden Ratio can be seen as a way to enter the quantum world, the world of subtle vibrations, in which we observe increasing energy levels as we move to smaller and smaller scales. El Nachie has proposed a way of calculating the fractal dimension of quantum space-time. The resulting value (Figure 7) suggests that the quantum world is composed of an infinite number or scaled copies of our ordinary 4-dimensional space-time.
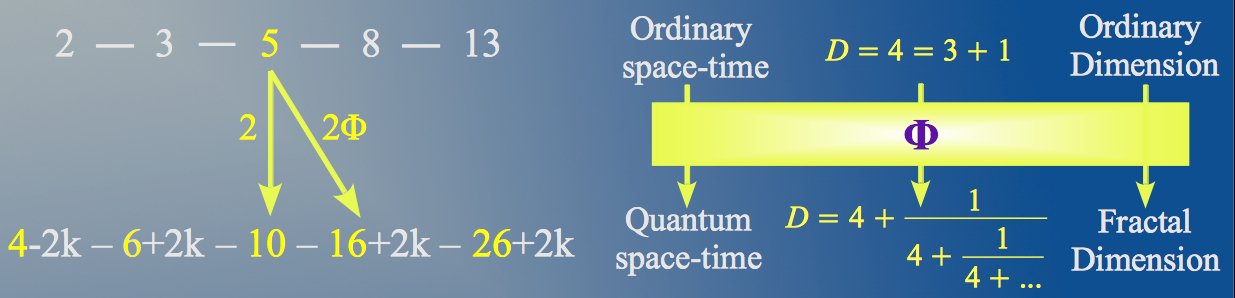 |
| Figure 7: The Golden Ratio seems to be the key that opens the door to the fractal quantum world, which looks as if there were an infinite number of scaled copies of our ordinary 4-dimensional space-time. |
3.- A fractal quantum space-time
3.1.- Brief overview
The main thesis of El Nachie is that, whereas space-time is linearly smooth and Euclidean at our usual scale and becomes curved at cosmic scales, at a quantum mechanical scale, as one comes nearer and nearer to Planck's length in the order of 10-33cm, space-time acquires a Cantor-set like structure, i.e. Euclidean geometry gives way to a highly non-linear fractal geometry [1]. El Nachie holds that all what we observe in nature is a manifestation of the true transfinite, fractal structure of quantum space-time underpinning it. The so-called E-infinity space is a topological-geometrical construct, according to which quantum space-time is an infinite dimensional hierarchical Cantor set whose stationary quantum states are given by the Vague Attractor of Kolmogorov or VAK (Figure 1):
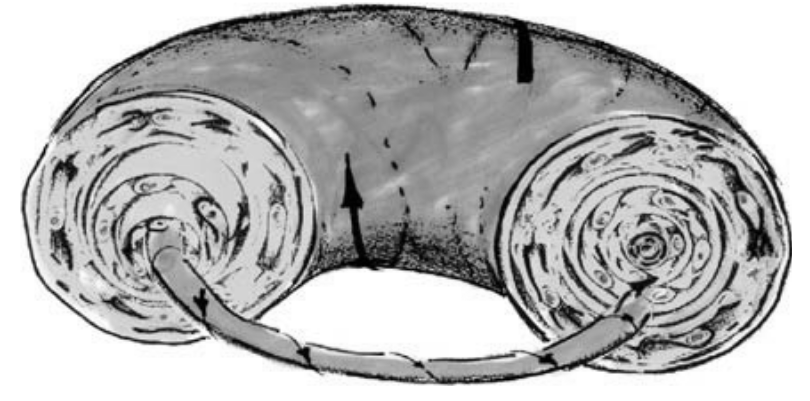 |
| Figure 8: An illustration of the Vague Attractor of Kolmogorov (VAK). |
Deterministic chaos is well documented in the literature, particularly in Hamiltonian systems connected to the work of Henri Poincaré. This pioneering work was then extended by Kolmogorov and others and finally led to the realization by the French topologist René Thom that the stationary states of quantum mechanics could be modeled by the VAK of Fig. 1. It is a composition of periodic orbits and chaotic islands which may be regarded as an extension of the notion of an attractor to Hamiltonian systems. The role of the stabilizing frictional forces, which is totally absent from Hamiltonian systems, and quantum mechanics is assumed here by the irrationality of the winding number. According to the KAM theorem (Kolmogorov, Arnold, Moser), the most stable periodic orbit of a dynamic system is that which has the Golden Ratio as a winding number. The more irrational the winding number is (the ratio of the resonance frequencies) the more stable is the periodic orbit. Since the Golden Ratio is the most irrational number, it follows that the orbit with the Golden Ratio as a winding number is the most stable. Therefore φ is the secret of the stability of most elementary particles. Vibration simulating particles which do not have a sufficient irrational winding number dissipate as fast as they are produced [2].
3.2.- The vacuum model
In E-infinity theory the vacuum is modelled as a hierarchical Cantor set formed through the union and intersection of an infinite number of elemetary Cantor sets, with a Hausdorff dimension directly related to the Golden Ratio. The simplest (Triadic) Cantor Set is constructed as follows (Figure 2). Consider the unit interval. Remove the middle third of this interval, except for the end points. We are now left with two intervals of length one third. Remove the middle third of each of the two left intervals, except again the end points. Repeating this process indefinitely, we are left with a point set that has no length, because we have removed almost the entire interval. Mathematicians refer to that as a point set of measure zero. In some sense there is nothing left anymore. Miraculously, however, this alleged nothingness has a respectable and relatively sizable dimension. Such point set dimension is called a Hausdorff (fractal) dimension, which in this case is equal to the natural logarithm of the number of parts left in each iteration divided by the number of divisions in each iteration. In our case this is ln 2 divided by ln 3 [1].
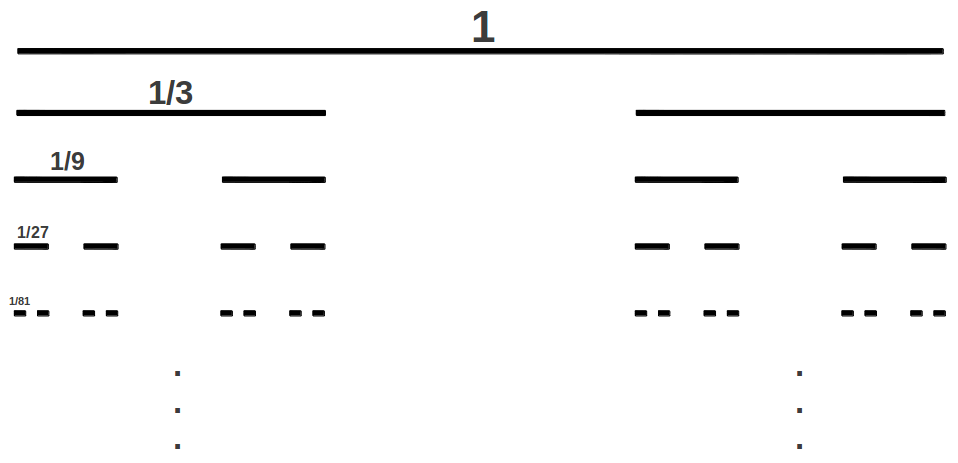 |
| Figure 9: Construction of the triadic Cantor set. In each iteration, the middle third of all the intervals is removed. |
The set this way constructed has a mathematical property which sounds unbelievable, but it is true: the number of points in our Cantor set is not one point less than the number of points in the original continuous-line interval. In both cases we have not only infinitely many points, but actually uncountable infinitely many points. It turns out that the Cantor set is a perfect compromise between the discrete and the continuum: it is a discrete structure, yet it has the same cardinality as the continuum.
Now suppose that the elementary Cantor set is formed randomly as follows (Figure 10). We choose a random value x from the original interval (0,1), and then we choose another random value y from the remaining subinterval (x,1). After removing the middle portion (x,y), we are left with two pieces (0,x) and (y,1) that have been chosen at random. Then this process is iterated indefinitely. According to the Mauldin-Williams theorem, it can be shown that the Hausdorff or fractal dimension of a random Cantor set is the inverse of the Golden Ratio 1/φ [3].
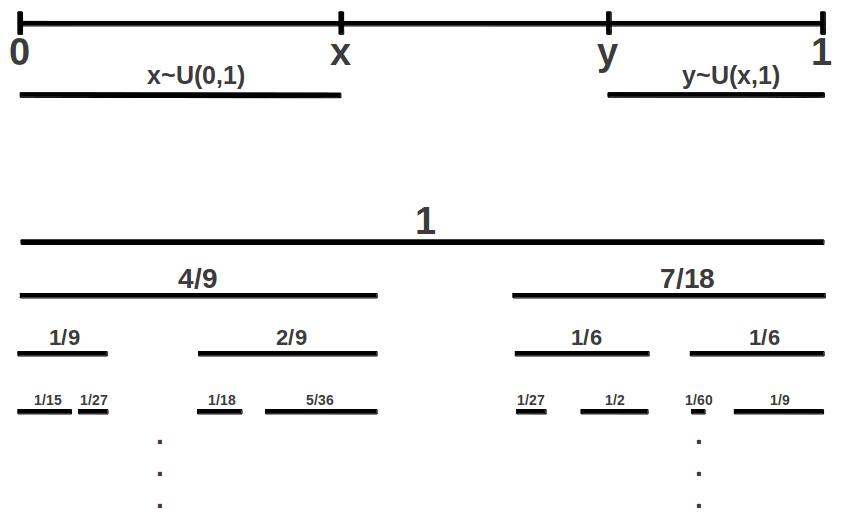 |
| Figure 10: Construction of a random Cantor set. In each iteration, the middle piece between two randomly selected values x and y is removed from all the intervals. |
Now imagine that we join an infinite number of such elementary random Cantor sets, with neither gaps nor overlapping. El Nachie has shown that, with this restriction, the dimension of each new set is a scaled 1/φ version of the previous one:
Under these conditions, the average Hausdorff (fractal) dimension D of the resulting set (the E-infinity space) is obtained by weighting and summing the dimensions of the infinite number of elementary random Cantor sets as follows:
This relationship can also be expressed as a continous fraction expansion:
which reminds us of the self-similarity of the VAK of Fig.1 and of ordinary fractals. El Nachie interprets this result as follows: whereas at low energy (at ordinary scale) space-time appears to be four dimensional -three space dimensions plus one time dimension- at unimaginable higher energy, i.e. when observing space-time at very small scales, much more than the electro weak unification, space-time will appear to have many more "small" dimensions. Some completely new, high resolution experimental setup may eventually prove the multidimensionality and basic fractality of quantum space-time beyond doubt.
It is worth noting that the average value which gives the dimension of the E-infinity space, D = 4 + 1/φ3 = φ3, coincides with the Hausdorff dimension dc = 1/φ of the original elementary random Cantor set, but lifted to four dimensions:
which means that, although the E-infinity space is infinite dimensional, seen from very far it gives the impression of being four dimensional and its Hausdorff and topological dimensions nearly coincide.
Physicist Carlos Castro holds that the connection of the exact average dimension of El Nachie's fractal quantum space-time to the Golden Ratio is not a simple numerical coincidence. He argues that there is a universial dimensional fluctuation in Nature given in terms of the Golden Ratio as
According to Castro [4], if we imagine the simmetry breaking from an original isotropic space with four equal dimensions with fluctuation, into a space with three spatial dimensions and one temporal dimension also with fluctuation, and we want to perceive them as our ordinary four dimensions, the fluctuation must be exactly:
This quantity is also related to Penrose tilings of the plane, like the one shown in Figure 11. If one would be standing at an arbitrary point there, then one would see the space around as a certain distinct pattern. Now if one moved an arbitrary distance, because the pattern is non-symmetric, in general one would have a different view of the pattern surrounding him at the new position. The question that arises is then: could it be that one could move to another point and still find oneself surrounded by the very same pattern once again? The surprising answer to this question is that we just need to move a distance not longer than the inverse of the Golden Ratio to the power of three divided by two. This is the so-called isomorphic length, and numerically happens to be exactly half the fractal dimension of E-infinity quantum space-time [1]:
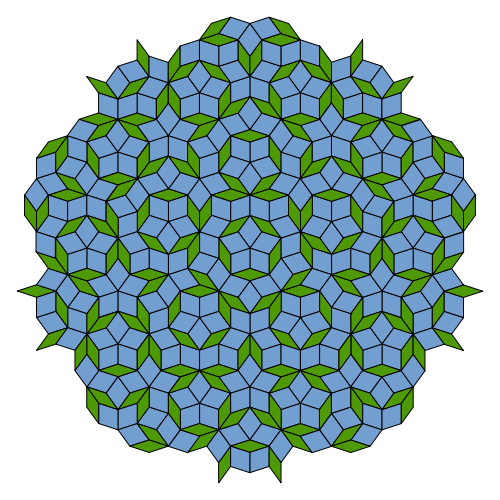 |
| Figure 11: A Penrose tiling of the plane. This non-periodic construction is formed by rotations and translations of two elemetary Golden Rhombi. |
3.3.- Geometrical visualizations
El Nachie offers the following two dimensional view of the E-infinity space. If we project the space-time of vacuum fluctuation on a Poincaré circle we will see a hyperbolic tessellation of this circle with predominantly Klein-curve-like geometry. It is an important part of El Naschie’s thesis that actually quantum space-time strongly resembles the hyperbolic geometry of Klein quartic (Figure 12). It is interesting to note that the polygon-like in the middle of Figure 12 resembles an heptagon, and as one increases the radius moving away from the origin there is an increasing number of such distorted and scaled heptagons which happens to be a multiple of 7. That reminds us of the continuous fraction expansion of φ4, which as we have seen is closely related to the Fine Structure constant.
 |
| Figure 12: An hyperbolic covering of the circle by a tiling of Klein quartic. The outer triangles are scaled an distorted versions of the central ones. El Nachie holds that, similarly, elementary particles are scaled and distorted versions of each other. |
This picture illustrates another fundamental tenet of El Nachie, who holds that all elementary particles are scaled and deformed versions of each other. He explains it as follows. Suppose that we stand somewhere towards the centre of the disk. And suppose we hold a neutron in our hand, so to speak. Then somewhere, towards the edge where everything ramifies at the finitely confined infinity, we may be observing an electron. His main thesis and the central piece of his picture he offers for an understanding of scaling in E-infinity, is that what appears to us to be an electron in the so-called reality is nothing but the neutron that we are holding. In other words, once we move to the spot where we are observing the electron, the whole world around us appears to be exactly the same once more. The minute we arrive at the electron everything, including ourselves and the ramified horizon at the edge of the circle, repeats itself as if we have not moved at all. In other words we find ourselves standing again with a neutron in our hands and watching an electron towards the border of the circle. This classically absurd and grotesque situation is precisely analogous to what we experience when we probe quantum space-time and the elementary particles inhabiting it on smaller and smaller distances using higher and higher energy [1].
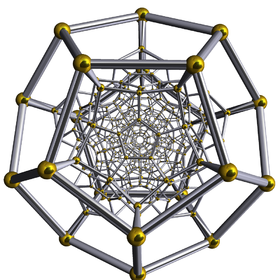 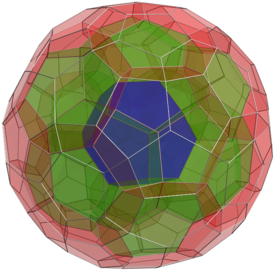 |
| Figure 13: The 120-cell Coxeter four dimensional polytop upon which the M4 hyperbolic manifold is based. E-infinity space-time may be regarded as a fuzzy version of M4. |
The internal structure of quantum space-time according to the E-infinity theory can also be geometrically visualized in higher dimensions. The starting point is the four-dimensional generalization of the dodecahedron, also known as the 120-cell Coxeter polytop. Similarly to what happens with the Tesseract which is the four-dimensional version of the cube, this polytop can be thought of as a dodecahedron each of whose faces has been replaced by another dodecahedron (Figure 13). From this polytop, an hyperbolic manifold M4 can be derived with an Euler characteristic χ(M4)=26 and a volume invariant Vol(M4)=684 [2]. A convenient fuzzy version M of this manifold adding the appropriate transfinite corrections leads to a model of E-infinity space-time. In this case, the topological invariants of M become:
This values should sound familiar to the reader. They have been introduced in Section 2 but in another context, namely the area-preserving transformation of a square into a rectangle following Golden Proportions (see Figure 4).
4.- The Fine Structure constant
The fractal space-time theory of El Nachie allows the exact determination of one of the fundamental quantities of physics, namely the Fine Structure constant, from a dimensional analysis. The resulting formula is as simple as [1]:
This formula can be further simplified and admits the following equivalent expressions:
We have already seen in Section 2 that the last expression admits a very simple geometrical interpretation in a polygon (Figure 4), and also as a fraction of the volume of a manifold derived from the generalization of the dodecahedron into four dimensions (Figure 13). The reader can easily check that these expressions have the same exact numerical value as the first one. This is the E-infinity low energy value, which is a genuine time-independent constant. This is so because in E-infinity of El Nachie's theory time is spacialized, i.e. there is no difference between time and space unlike our 3 + 1 space–time with time symmetry breaking introduced. Thus, seen from our 3 + 1 space–time, we need to use a projection in order to cure a slight local aberration or misfit. That way we "project" the E-infinity value onto 3 + 1 space in a manner of speaking. The so-obtained value is almost identical to that obtained experimentally:
where k0=1/φ5·(1-1/φ5), which agrees with CODATA value with an error as small as ± 0.00001%. In our article on the Golden Ratio in Atomic Structure we offered an alternative formula for the Fine Structure constant in terms of the Golden Angle which also was in excellent agreement with the experimentally observed value, but the error was an order of magnitude higher (0.00027%).
4.- The mass-energy of fundamental particles
A note on units: Many scientists have the view that the choice of units is crucial to solve a given problem, and that it should be based as far as possible on fundamental constans of Nature. In our case, everything seems to suggest that the right units for the energy of elemetary particles are eV (electron-Volts). Actually, we will see that all of the proposed formulas give the expected value for the physical quantity involved in MeV. It appears that Nature has chosen these specific units for measuring the energy elementary particles. Particle physicists use this unit also as a measure of mass, because they have in mind that mass and energy are related through Einstein formula E=mc2. Therefore we use the term mass-energy.
The following table summarizes the Golden Ratio-based theoretical expressions for the mass-energy of some elemental particles obtained through El Nachie's theory. We can see that in general there is a good agreement with their corresponding experimental values. In the case of the electron, a correction is needed similar to that for the Fine Structure constant, in order to take into account the symmetry breaking of space-time in the transit from low to high scale.
| Particle | Theoretical mass-energy formula |
Numerical value (MeV) |
Experimental value (MeV) |
Error (%) |
|---|---|---|---|---|
|
Electron (e-) |
0.5116673 | 0.5109989 | 0.00146 | |
|
Neutron (n) |
939.574275 | 939.565379 | 0.00095 | |
|
Proton (p+) |
938.269323 | 938.272046 | 0.00029 | |
|
Charged Pion (π±) |
139.5820393 | 139.57018 | 0.0085 | |
|
Neutral Pion (π0) |
134.5820393 | 134.97660 | 0.2923 | |
|
Tau (τ) |
177.4829191 | 1776.82 | 0.01897 | |
| Muon (μ) | 105.3098758 | 105.658375 | 0.32983 |
5.- The connection with string theory
One of the most promising attempts to go beyond the standard model of particle physics is superstring theory. As it is well known, special relativity fused time and space together, then came general relativity and introduced a curvature to space-time. Kaluza and later on Klein added one more dimension to the classical four in order to unify general relativity and electromagnetism. The dimensionality of space-time plays a paramount role in the theoretical physics of unification and has led to the introduction of the 26 dimensions of string theory, the 10 dimensions of superstring theory, and finally the heterotic string theory with the dimensional hierarchy 4, 6, 10, 16 and 26 [2].
String theory holds that all elementary particles are nothing but the different modes of string vibrations. E-infinity theory claims to go one step further and imagines these strings to have a fine structure, more precisely it conceives these strings as being made of Cantor sets. The vibration is understood as a sizzling violent movement of transfinite (fractal) sets simulating the so-called vacuum fluctuation. Seen from far, the sizzling Cantor sets appear as if they were the violent movement of superstrings, and these strings seen from farther appear as if they were particles.
According to El Nachie, the fact that heterotic superstrings are embedded in E-infinity may be deduced from the following incredible scaling of the Fine Structure constant:
Setting k=0 one obtains the classical dimensions of heterotic superstring theory, namely 26, 16, 10, 6 and 4, as well as the constant of super-symmetric (αgs=26) and non super-symmetric (αg=42) unification of all fundamental forces. As we have seen in section 2, the above is a Fibonacci-like sequence with a very concise geometrical interpetation related to numbers 5, 11 and φ.
10/10/2012
References
[1] El Naschie MS. "VAK, vacuum fluctuation and the mass spectrum of high energy particle physics". Chaos, Solitons & Fractals 2003;17:797–807.
[2] Marek-Crnjac, L. "A short history of fractal-Cantorian space-time", Chaos, Solitons and Fractals, vol.41, pp.2697–2705, 2009.
[3] Mauldin R.D., Williams S.C.: "Random Recursive Constructions: Asymptotic Geometric and Topological properties", Transactions of the American Mathematical Society, Vol. 295(1), May 1986.
[4] Castro, Carlos, "On the four-dimensional conformal anomaly fractal Cantorian space-time and the fine structure constant", Chaos, Solitons and Fractals, vol. 13, pp.203-207, 2002.
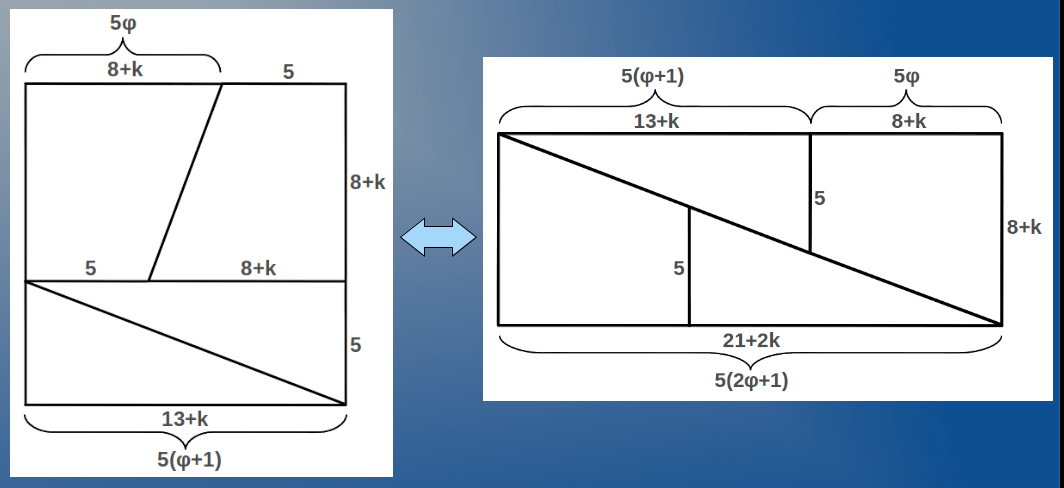
The missing area
The following figure shows where the lost unit of area was hidden in the transformation process from a square to a rectangle (Section 2):